甘肃省定西市岷县2022-2023学年七年级上学期开学数学试卷(一)
试卷更新日期:2022-09-27 类型:开学考试
一、选择题(本题共10小题,共30分)
-
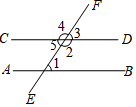
1. 下列各数: , , , , , 其中无理数有( )A、4个 B、3个 C、2个 D、1个2. 在平面直角坐标系中,已知点 , 则点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 如图,下列判断中正确的是( )
 A、如果 , 那么 B、如果 , 那么 C、如果 , 那么 D、如果 , 那么4. 已知和是方程的解,则 , 的值为( )A、 , B、 , C、 , D、 ,5. 方程组 的解是( )A、 B、 C、 D、6. 下列调查中,最适合采用全面调查(普查)的是( )A、对我市中学生每周课外阅读时间情况的调查 B、对我市市民知晓“礼让行人”交通新规情况的调查 C、对我市中学生观看电影《厉害了,我的国》情况的调查 D、对我国首艘国产航母002型各零部件质量情况的调查7. 已知不等式 , 其解集在数轴上表示正确的是( )A、
A、如果 , 那么 B、如果 , 那么 C、如果 , 那么 D、如果 , 那么4. 已知和是方程的解,则 , 的值为( )A、 , B、 , C、 , D、 ,5. 方程组 的解是( )A、 B、 C、 D、6. 下列调查中,最适合采用全面调查(普查)的是( )A、对我市中学生每周课外阅读时间情况的调查 B、对我市市民知晓“礼让行人”交通新规情况的调查 C、对我市中学生观看电影《厉害了,我的国》情况的调查 D、对我国首艘国产航母002型各零部件质量情况的调查7. 已知不等式 , 其解集在数轴上表示正确的是( )A、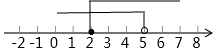 B、
B、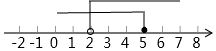 C、
C、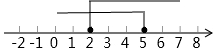 D、
D、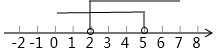 8. 关于 , 的方程组 的解满足 ,则 的取值范围是( )A、 B、 C、 D、9. 为了了解本校八年级学生的体能情况,随机抽查了其中30名学生,测试了仰卧起坐次数,并绘制如图所示的频数分布直方图,请根据图中的信息,计算仰卧起坐次数在∽次的百分比是( )
8. 关于 , 的方程组 的解满足 ,则 的取值范围是( )A、 B、 C、 D、9. 为了了解本校八年级学生的体能情况,随机抽查了其中30名学生,测试了仰卧起坐次数,并绘制如图所示的频数分布直方图,请根据图中的信息,计算仰卧起坐次数在∽次的百分比是( )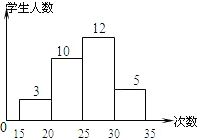 A、40% B、30% C、20% D、10%10. 小明在拼图时发现8个一样大小的长方形恰好拼成一个大的长方形,如图1所示.小红看见了,说:“我也来试一试.“结果小红七拼八凑,拼成如图2那样的正方形,但中间留下了一个洞,恰好是边长为的小正方形,则每个小长方形的长和宽分别为( )
A、40% B、30% C、20% D、10%10. 小明在拼图时发现8个一样大小的长方形恰好拼成一个大的长方形,如图1所示.小红看见了,说:“我也来试一试.“结果小红七拼八凑,拼成如图2那样的正方形,但中间留下了一个洞,恰好是边长为的小正方形,则每个小长方形的长和宽分别为( ) A、 , B、 , C、 , D、 ,
A、 , B、 , C、 , D、 ,二、填空题(本题共6小题,共18分)
-
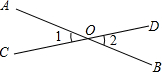
11. 如图,直线与相交于点 , 且 , 的度数为 .
 12. 计算: .
12. 计算: .
13. 点向上平移3个单位长度得到的点的坐标是 .14. 对于实数 , , 定义运算“”: , 例如 , 因为 , 所以若 , 满足方程组 , 则 .15. 小明做作业时,不小心将方程中的一个常数污染了看不清楚,小芳告诉他该方程的解是负数,并且这个常数是负整数,该方程的解是 .16. 如图是根据某校为地震灾区捐款的情况而制作的统计图,已知该校在校学生有600人,请根据统计图计算该校共捐款元.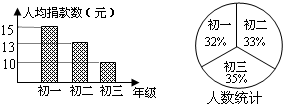
三、解答题(本题共9小题,共72分)
-
17. 解下列方程组:(1)、(2)、18. 解下列不等式组 , 并把它们的解集在数轴上表示出来:(1)、(2)、19. 如图1,将三角形平移,使沿的延长线移至得到三角形 , 交于点 , 平分 .
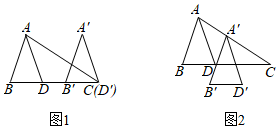 (1)、猜想与之间的关系,并写出理由;(2)、将三角形平移至如图所示位置,得到三角形 , 请问:平分吗?为什么?20. 如图,在长方形中,为平面直角坐标系的原点,点、的坐标分别为、 , 点在第一象限.
(1)、猜想与之间的关系,并写出理由;(2)、将三角形平移至如图所示位置,得到三角形 , 请问:平分吗?为什么?20. 如图,在长方形中,为平面直角坐标系的原点,点、的坐标分别为、 , 点在第一象限.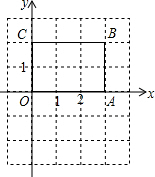 (1)、写出点的坐标;(2)、若过点的直线交长方形的边于点 , 且把长方形的周长分成2:3的两部分,求点的坐标.21. 一个被墨水污染了的方程组: , 小明回忆道:“这个方程组的解是 , 而我求的解是 , 经检验后发现,我的错误是由于看错了第二个方程中的系数所致”根据小明的回忆,你能求出原方程组吗?22. 已知实数 , 满足 .(1)、用含的代数式表示;(2)、若实数满足 , 求的取值范围;(3)、实数 , 满足 , 且 , , 求的取值范围.23. 随着人们生活水平的不断提高,人们对生活饮用水质量要求也越来越高,更多的居民选择购买家用净水器.一商家抓住商机,从生产厂家购进了 , 两种型号家用净水器.已知购进2台型号家用净水器比1台型号家用净水器多用200元;购进3台型号净水器和2台型号家用净水器共用6600元,(1)、求 , 两种型号家用净水器每台进价各为多少元?(2)、该商家用不超过26400元共购进 , 两种型号家用净水器20台,再将购进的两种型号家用净水器分别加价50%后出售,若两种型号家用净水器全部售出后毛利润不低于12000元,求商家购进 , 两种型号家用净水器各多少台?注:毛利润售价进价24. 为了掌握八年级数学考试卷的命题质量与难度系数,命题组教师赴外地选取一个水平相当的八年级班级进行预测,将考试成绩分布情况进行处理分析,制成频数分布表如下成绩得分均为整数:
(1)、写出点的坐标;(2)、若过点的直线交长方形的边于点 , 且把长方形的周长分成2:3的两部分,求点的坐标.21. 一个被墨水污染了的方程组: , 小明回忆道:“这个方程组的解是 , 而我求的解是 , 经检验后发现,我的错误是由于看错了第二个方程中的系数所致”根据小明的回忆,你能求出原方程组吗?22. 已知实数 , 满足 .(1)、用含的代数式表示;(2)、若实数满足 , 求的取值范围;(3)、实数 , 满足 , 且 , , 求的取值范围.23. 随着人们生活水平的不断提高,人们对生活饮用水质量要求也越来越高,更多的居民选择购买家用净水器.一商家抓住商机,从生产厂家购进了 , 两种型号家用净水器.已知购进2台型号家用净水器比1台型号家用净水器多用200元;购进3台型号净水器和2台型号家用净水器共用6600元,(1)、求 , 两种型号家用净水器每台进价各为多少元?(2)、该商家用不超过26400元共购进 , 两种型号家用净水器20台,再将购进的两种型号家用净水器分别加价50%后出售,若两种型号家用净水器全部售出后毛利润不低于12000元,求商家购进 , 两种型号家用净水器各多少台?注:毛利润售价进价24. 为了掌握八年级数学考试卷的命题质量与难度系数,命题组教师赴外地选取一个水平相当的八年级班级进行预测,将考试成绩分布情况进行处理分析,制成频数分布表如下成绩得分均为整数:组别
成绩分组
频数
百分比
1
2
5%
2
4
10%
3
20%
4
10
25%
5
6
15%
合计
40
100%
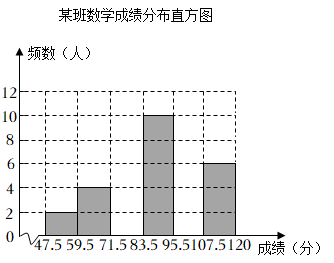
根据表中提供的信息解答下列问题:
(1)、频数分布表中的 , , ;(2)、已知全区八年级共有200个班平均每班40人 , 用这份试卷检测,108分及以上为优秀,预计优秀的人数约为人,72分及以上为及格,预计及格的人数约为人,及格的百分比约为;(3)、补充完整频数分布直方图.25. P是三角形内一点,射线 , 射线 .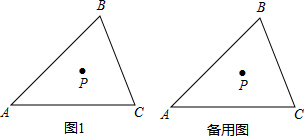 (1)、当点 , 分别在 , 上时,
(1)、当点 , 分别在 , 上时,①补全图1;
②猜想与的数量关系,并证明;
(2)、当点 , 都在线段上时,你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.