甘肃省定西市岷县2022-2023学年八年级上学期开学数学试卷(一)
试卷更新日期:2022-09-27 类型:开学考试
一、选择题(本大题共10小题,共30分。)
-
1. 下列二次根式中,是最简二次根式是( )A、 B、 C、 D、2. 下列各曲线表示的与的关系中,不是的函数的是( )A、
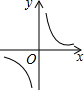 B、
B、 C、
C、 D、
D、 3. 在下列图形性质中,平行四边形不一定具备的是( )A、对角线相等 B、两组对边分别平行 C、两组对边分别相等 D、对角线互相平分4. 甲、乙两名运动员在相同的条件下,各射击10次,经过计算,甲、乙两人成绩的平均数均是9.5环,甲的成绩的方差是0.125,乙的成绩的方差是1.85,那么这10次射击中,甲、乙成绩的稳定情况是( )A、甲较为稳定 B、乙较为稳定 C、两个人成绩一样稳定 D、不能确定5. 平行四边形中两个内角的度数比是1:3,则其中较小的内角是( )A、 B、 C、 D、6. 如图,函数和的图象相交于点 , 则不等式的解集为( )
3. 在下列图形性质中,平行四边形不一定具备的是( )A、对角线相等 B、两组对边分别平行 C、两组对边分别相等 D、对角线互相平分4. 甲、乙两名运动员在相同的条件下,各射击10次,经过计算,甲、乙两人成绩的平均数均是9.5环,甲的成绩的方差是0.125,乙的成绩的方差是1.85,那么这10次射击中,甲、乙成绩的稳定情况是( )A、甲较为稳定 B、乙较为稳定 C、两个人成绩一样稳定 D、不能确定5. 平行四边形中两个内角的度数比是1:3,则其中较小的内角是( )A、 B、 C、 D、6. 如图,函数和的图象相交于点 , 则不等式的解集为( ) A、 B、 C、 D、7. 在中,周长为60,斜边与一条直角边之比为13:5,则这个直角三角形的三边长分别为( )A、26,24,10 B、13,12,5 C、20,16,24 D、25,20,158. 如图,矩形的对角线、相交于点 , , , , 若 , 则四边形的周长为( )
A、 B、 C、 D、7. 在中,周长为60,斜边与一条直角边之比为13:5,则这个直角三角形的三边长分别为( )A、26,24,10 B、13,12,5 C、20,16,24 D、25,20,158. 如图,矩形的对角线、相交于点 , , , , 若 , 则四边形的周长为( ) A、4 B、8 C、10 D、129. 已知,在平面直角坐标系中,点 , 点在直线上.当 , 两点间的距离最小时,点的坐标是( )A、 B、 C、 D、10. 如图①,在平面直角坐标系中,平行四边形在第一象限,轴,直线从原点出发沿轴正方向平移,被平行四边形截得的线段的长度与平移的距离的函数图象如图②所示,那么平行四边形的面积为( )
A、4 B、8 C、10 D、129. 已知,在平面直角坐标系中,点 , 点在直线上.当 , 两点间的距离最小时,点的坐标是( )A、 B、 C、 D、10. 如图①,在平面直角坐标系中,平行四边形在第一象限,轴,直线从原点出发沿轴正方向平移,被平行四边形截得的线段的长度与平移的距离的函数图象如图②所示,那么平行四边形的面积为( ) A、 B、12 C、 D、6
A、 B、12 C、 D、6二、填空题(本大题共6小题,共18分)
-
11. 函数中,自变量的取值范围是 .12. 如图,中,于 , 是的中点.若 , , 则的长等于 .
 13. 已知 , 是一次函数的图象上的两个点,则 , 的大小关系是 .14. 已知关于的方程的解为 , 则一次函数与轴交点的坐标为 .15. 在Rt△ABC中,∠C=90°,D为BC上的一点,AD=BD=2,AB= ,则AC的长为 .16. 如图,在矩形中, , , 若点在边上,连接、 , 是以为腰的等腰三角形,则的长为 .
13. 已知 , 是一次函数的图象上的两个点,则 , 的大小关系是 .14. 已知关于的方程的解为 , 则一次函数与轴交点的坐标为 .15. 在Rt△ABC中,∠C=90°,D为BC上的一点,AD=BD=2,AB= ,则AC的长为 .16. 如图,在矩形中, , , 若点在边上,连接、 , 是以为腰的等腰三角形,则的长为 .
三、解答题(本大题共10小题,共72分。)
-
17. 计算: .18. 已知函数(1)、若函数图象经过原点,求的值;(2)、若函数的图象平行于直线 , 求的值(3)、若这个函数是一次函数,且随着的增大而增大,且不经过第二象限,求的取值范围.19. 如图,在▱中,以点为圆心,长为半径画弧交于点 , 再分别以点、为圆心,大于的相同长为半径画弧,两弧交于点;连接并延长交于点 , 连接 .
 (1)、根据以上尺规作图的过程,证明四边形是菱形;(2)、若菱形的边长为 , , 求菱形的面积.20. 为了分析某节复习课的教学效果,上课前,张老师让901班每位同学做6道题目与这节课内容相关 , 解题情况如图所示:上课后,再让学生做6道类似的题目,结果如表所示.已知每位学生至少答对1题.
(1)、根据以上尺规作图的过程,证明四边形是菱形;(2)、若菱形的边长为 , , 求菱形的面积.20. 为了分析某节复习课的教学效果,上课前,张老师让901班每位同学做6道题目与这节课内容相关 , 解题情况如图所示:上课后,再让学生做6道类似的题目,结果如表所示.已知每位学生至少答对1题.上课后解题情况频数统计表
答对题数
频数人
1
2
2
3
3
3
4
10
5
9
6
13
 (1)、901班有多少名学生?(2)、该班上课前解题时答对题数的中位数是多少?(3)、请选择适当的统计量,从两个不同的角度评价这节复习课的教学效果.21. 已知,如图,在中,是的中点, , 垂足为 , 交于点 , 且 ,
(1)、901班有多少名学生?(2)、该班上课前解题时答对题数的中位数是多少?(3)、请选择适当的统计量,从两个不同的角度评价这节复习课的教学效果.21. 已知,如图,在中,是的中点, , 垂足为 , 交于点 , 且 , (1)、求证: .(2)、若 , , 求的长.22. 如图,已知自行车与摩托车从甲地开往乙地,与分别表示它们与甲地距离千米与时间小时的关系,则:
(1)、求证: .(2)、若 , , 求的长.22. 如图,已知自行车与摩托车从甲地开往乙地,与分别表示它们与甲地距离千米与时间小时的关系,则: (1)、摩托车每小时走千米,自行车每小时走千米;(2)、自行车出发后多少小时,它们相遇?(3)、摩托车出发后多少小时,他们相距10千米?23. 如图,已知正方形 , 是对角线上任意一点,为上的点,且 , , .
(1)、摩托车每小时走千米,自行车每小时走千米;(2)、自行车出发后多少小时,它们相遇?(3)、摩托车出发后多少小时,他们相距10千米?23. 如图,已知正方形 , 是对角线上任意一点,为上的点,且 , , . (1)、求证:四边形是正方形;(2)、求证: .24. 如图,▱的对角线、相交于点 , , , 点在线段上从点以的速度向点运动,点在线段上从点以的速度向点运动.
(1)、求证:四边形是正方形;(2)、求证: .24. 如图,▱的对角线、相交于点 , , , 点在线段上从点以的速度向点运动,点在线段上从点以的速度向点运动. (1)、若点、同时运动,设运动时间为秒,当为何值时,四边形是平行四边形.(2)、在(1)的条件下,当为何值时,▱是菱形;(3)、求(2)中菱形的面积.25. 为了贯彻落实市委政府提出的“精准扶贫”精神,某校特制定了一系列帮扶A、B两贫困村的计划,现决定从某地运送152箱鱼苗到A、B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如表:
(1)、若点、同时运动,设运动时间为秒,当为何值时,四边形是平行四边形.(2)、在(1)的条件下,当为何值时,▱是菱形;(3)、求(2)中菱形的面积.25. 为了贯彻落实市委政府提出的“精准扶贫”精神,某校特制定了一系列帮扶A、B两贫困村的计划,现决定从某地运送152箱鱼苗到A、B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如表:车型 目的地 A村(元/辆) B村(元/辆) 大货车 800 900 小货车 400 600
(1)、求这15辆车中大小货车各多少辆?(2)、现安排其中10辆货车前往A村,其余货车前往B村,设前往A村的大货车为x辆,前往A、B两村总费用为y元,试求出y与x的函数解析式.(3)、在(2)的条件下,若运往A村的鱼苗不少于100箱,请你写出使总费用最少的货车调配方案,并求出最少费用.26. 如图,在平面直角坐标系中,矩形的边在轴上, , , 经过点的直线与轴、轴分别交于点、 . (1)、求:①点的坐标;②经过点 , 且与直线平行的直线的函数表达式;(2)、直线上是否存在点 , 使得为等腰直角三角形?若存在,求出点的坐标;若不存在,请说明理由.(3)、在平面直角坐标系内确定点 , 使得以点、、、为顶点的四边形是平行四边形,请直接写出点的坐标.
(1)、求:①点的坐标;②经过点 , 且与直线平行的直线的函数表达式;(2)、直线上是否存在点 , 使得为等腰直角三角形?若存在,求出点的坐标;若不存在,请说明理由.(3)、在平面直角坐标系内确定点 , 使得以点、、、为顶点的四边形是平行四边形,请直接写出点的坐标.