四川省绵阳市三台县2021-2022学年九年级上学期期中数学试题
试卷更新日期:2022-09-27 类型:期中考试
一、单选题
-
1. 下列标志既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、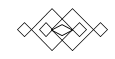 2. 如图,的三个顶点都在方格纸的格点上,其中点A的坐标是 . 现将绕点A顺时针旋转90°,则旋转后点C的坐标是( )
2. 如图,的三个顶点都在方格纸的格点上,其中点A的坐标是 . 现将绕点A顺时针旋转90°,则旋转后点C的坐标是( ) A、 B、 C、 D、3. 关于x的一元二次方程(a﹣1)x2﹣x+a2﹣1=0的一个根是0,则a的值为( )A、1或﹣1 B、﹣1 C、1 D、4. 将抛物线y=﹣2(x+3)2+1向左平移2个单位,再向上平移1个单位后所得到的抛物线的解析式为( )A、y=2(x+1)2 B、y=﹣2(x+5)2+2 C、y=﹣2(x+5)2+3 D、y=﹣2(x﹣5)2﹣15. 已知关于 的方程 ,下列说法正确的是( )A、当 时,方程无解 B、当 时,方程有一个实数解 C、当 时,方程有两个相等的实数解 D、当 时,方程总有两个不相等的实数解6. 用配方法解方程 , 方程应变形为( )A、 B、 C、 D、7. 如图是一位同学从照片上剪切下来的海上日出时的画面,“图上”太阳与海平线交于A,B两点,他测得“图上”圆的半径为10厘米,厘米.若从目前太阳所处位置到太阳完全跳出海平面的时间为16分钟,则“图上”太阳升起的速度为( )
A、 B、 C、 D、3. 关于x的一元二次方程(a﹣1)x2﹣x+a2﹣1=0的一个根是0,则a的值为( )A、1或﹣1 B、﹣1 C、1 D、4. 将抛物线y=﹣2(x+3)2+1向左平移2个单位,再向上平移1个单位后所得到的抛物线的解析式为( )A、y=2(x+1)2 B、y=﹣2(x+5)2+2 C、y=﹣2(x+5)2+3 D、y=﹣2(x﹣5)2﹣15. 已知关于 的方程 ,下列说法正确的是( )A、当 时,方程无解 B、当 时,方程有一个实数解 C、当 时,方程有两个相等的实数解 D、当 时,方程总有两个不相等的实数解6. 用配方法解方程 , 方程应变形为( )A、 B、 C、 D、7. 如图是一位同学从照片上剪切下来的海上日出时的画面,“图上”太阳与海平线交于A,B两点,他测得“图上”圆的半径为10厘米,厘米.若从目前太阳所处位置到太阳完全跳出海平面的时间为16分钟,则“图上”太阳升起的速度为( ) A、1.0厘米/分 B、0.8厘米/分 C、1.2厘米/分 D、1.4厘米/分8. 宾馆有间房供游客居住,当每间房每天定价为元时,宾馆会住满;当每间房每天的定价每增加元时,就会空闲一间房.如果有游客居住,宾馆需对居住的每间房每天支出元的费用.设房价定为元,宾馆当天利润为元.则可列方程( )A、 B、 C、 D、9. 已知一次函数y=x+c的图象如图,则二次函数y=ax2+bx+c在平面直角坐标系中的图象可能是( )
A、1.0厘米/分 B、0.8厘米/分 C、1.2厘米/分 D、1.4厘米/分8. 宾馆有间房供游客居住,当每间房每天定价为元时,宾馆会住满;当每间房每天的定价每增加元时,就会空闲一间房.如果有游客居住,宾馆需对居住的每间房每天支出元的费用.设房价定为元,宾馆当天利润为元.则可列方程( )A、 B、 C、 D、9. 已知一次函数y=x+c的图象如图,则二次函数y=ax2+bx+c在平面直角坐标系中的图象可能是( )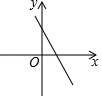 A、
A、 B、
B、 C、
C、 D、
D、 10. 如图,已知∠BAC=60°,AB=4,AC=6,点P在△ABC内,将APC绕着点A逆时针方向旋转60°得到AEF.则AE+PB+PC的最小值为( )
10. 如图,已知∠BAC=60°,AB=4,AC=6,点P在△ABC内,将APC绕着点A逆时针方向旋转60°得到AEF.则AE+PB+PC的最小值为( )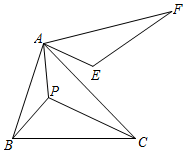 A、2 B、8 C、5 D、611. 如图,利用一个直角墙角修建一个梯形储料场ABCD,其中∠C=120°.若新建墙BC与CD总长为12m,则该梯形储料场ABCD的最大面积是( )
A、2 B、8 C、5 D、611. 如图,利用一个直角墙角修建一个梯形储料场ABCD,其中∠C=120°.若新建墙BC与CD总长为12m,则该梯形储料场ABCD的最大面积是( ) A、18m2 B、m2 C、m2 D、m212. 二次函数的部分图象如图所示,图象过点 , 对称轴为直线 , 下列结论:
A、18m2 B、m2 C、m2 D、m212. 二次函数的部分图象如图所示,图象过点 , 对称轴为直线 , 下列结论:①;
②;
③;
④若点、点、点在该函数图象上,则;
⑤若方程的两根为和 , 且 , 则;
其中正确的结论是( )
 A、①③⑤ B、①④⑤ C、①②④ D、①⑤
A、①③⑤ B、①④⑤ C、①②④ D、①⑤二、填空题
-
13. 方程的解是 .14. 设 是关于x的方程 的两个根,且 ,则 .15. 如图,的直径BA的延长线与弦DC的延长线交于点E,且 , 已知 , 则等于 .
 16. 如图,在四边形ABCD中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,则BD的长为.
16. 如图,在四边形ABCD中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,则BD的长为. 17. 已知函数y的图象如图所示,若直线y=kx﹣3与该图象有公共点,则k的最大值与最小值的和为 .
17. 已知函数y的图象如图所示,若直线y=kx﹣3与该图象有公共点,则k的最大值与最小值的和为 . 18. 如图,已知直线y=x+1与y轴交于点A,与x轴交于点D,抛物线y= x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).在抛物线的对称轴上找一点M,使|AM﹣MC|的值最大,求出点M的坐标.
18. 如图,已知直线y=x+1与y轴交于点A,与x轴交于点D,抛物线y= x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).在抛物线的对称轴上找一点M,使|AM﹣MC|的值最大,求出点M的坐标.
三、解答题
-
19.(1)、解方程: .(2)、先化简,再求值: , 其中x满足方程: .20. 已知关于x的两个一元二次方程:
方程①:;
方程②: .
(1)、若方程①有两个相等的实数根,求k的值.(2)、若方程①和②只有一个方程有实数根,请说明此时哪个方程没有实数根.(3)、在(2)中若一定有实数根的那个方程的两根分别为、 , 且两根的平方和为3(即)中,求k的值.21. 如图①是一条抛物线形状的拱桥,水面宽AB为6米,拱顶C离水面的距离为4米. (1)、建立恰当的坐标系,并求出抛物线的解析式;(2)、一艘货船的截面如图②所示,它是由一个正方形MNEF和一个梯形KLGH组成的轴对称图形,货船的宽度KH为5米,货物高度MN为3米.若船弦离水面的安全距离为0.25米,请问货船能否安全通过桥洞?说明理由.22. 如图,在半径为2的扇形OAB中, , 点C是上的一个动点(不与点A,B重合), , , 垂足分别为D,E.
(1)、建立恰当的坐标系,并求出抛物线的解析式;(2)、一艘货船的截面如图②所示,它是由一个正方形MNEF和一个梯形KLGH组成的轴对称图形,货船的宽度KH为5米,货物高度MN为3米.若船弦离水面的安全距离为0.25米,请问货船能否安全通过桥洞?说明理由.22. 如图,在半径为2的扇形OAB中, , 点C是上的一个动点(不与点A,B重合), , , 垂足分别为D,E. (1)、当时,求线段OD的长;(2)、在中,是否存在长度保持不变的边?如果存在,请指出并求其长度;如果不存在,请说明理由.(3)、在中,是否存在度数保持不变的角?如果存在,请指出并求其度数;如果不存在,请说明理由.23. 在△ABC中,BA=BC,D,E是AC边上的两点,且满足∠DBE=∠ABC.
(1)、当时,求线段OD的长;(2)、在中,是否存在长度保持不变的边?如果存在,请指出并求其长度;如果不存在,请说明理由.(3)、在中,是否存在度数保持不变的角?如果存在,请指出并求其度数;如果不存在,请说明理由.23. 在△ABC中,BA=BC,D,E是AC边上的两点,且满足∠DBE=∠ABC. (1)、如图1,以点B为旋转中心,将△EBC按逆时针方向旋转,得到△E′BA(点C与点A重合,点E到点E′处),连接DE′.求证:DE′=DE;(2)、如图2,若∠ABC=90°,AD=4,EC=2,求DE的长.24. 九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
(1)、如图1,以点B为旋转中心,将△EBC按逆时针方向旋转,得到△E′BA(点C与点A重合,点E到点E′处),连接DE′.求证:DE′=DE;(2)、如图2,若∠ABC=90°,AD=4,EC=2,求DE的长.24. 九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:时间x(天)
1≤x<50
50≤x≤90
售价(元/件)
x+40
90
每天销量(件)
200-2x
已知该商品的进价为每件30元,设销售该商品的每天利润为y元[
(1)、求出y与x的函数关系式;(2)、问销售该商品第几天时,当天销售利润最大,最大利润是多少?(3)、该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.25. 如图,在平面直角坐标系中,抛物线与x轴交于点A、B,与y轴交于点C,连接BC, , 对称轴为直线 , 点D为此抛物线的顶点. (1)、求抛物线的解析式;(2)、点E是第一象限内抛物线上的动点,连接BE和CE,求面积的最大值;(3)、点P在抛物线对称轴上,平面内存在点Q,使以点B、C、P、Q为顶点的四边形为矩形,请直接写出点Q的坐标.
(1)、求抛物线的解析式;(2)、点E是第一象限内抛物线上的动点,连接BE和CE,求面积的最大值;(3)、点P在抛物线对称轴上,平面内存在点Q,使以点B、C、P、Q为顶点的四边形为矩形,请直接写出点Q的坐标.