四川省绵阳市江油市2021-2022学年九年级上学期期中数学试题
试卷更新日期:2022-09-27 类型:期中考试
一、单选题
-
1. 下列安全标志图中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 关于x的一元二次方程x2﹣2x+k+2=0有实数根,则k的取值范围在数轴上表示正确的是( )A、
2. 关于x的一元二次方程x2﹣2x+k+2=0有实数根,则k的取值范围在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 3. 用配方法解方程 ,变形后的结果正确的是( )A、 B、 C、 D、4. 某品牌服装原价173元,连续两次降价x%后售价为127元,下面所列方程中正确的是( )A、 B、 C、 D、5. 如图,某小区计划在一块长为32m,宽为20m的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570m2 . 若设道路的宽为xm,则下面所列方程正确的是( ).
3. 用配方法解方程 ,变形后的结果正确的是( )A、 B、 C、 D、4. 某品牌服装原价173元,连续两次降价x%后售价为127元,下面所列方程中正确的是( )A、 B、 C、 D、5. 如图,某小区计划在一块长为32m,宽为20m的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570m2 . 若设道路的宽为xm,则下面所列方程正确的是( ). A、(32﹣2x)(20﹣x)=570 B、32x+2×20x=32×20﹣570 C、(32﹣x)(20﹣x)=32×20﹣570 D、32x+2×20x﹣2x2=5706. 学校早上8:20上第一节课,40分钟后下课,这节课中分针转动的角度为( )A、180° B、240° C、270° D、200°7. 把抛物线向左平移2个单位,再向上平移1个单位,再绕原点旋转180°所得的抛物线的解析式是( )A、 B、 C、 D、8. 在羽毛球比赛中,某次羽毛球的运动路线可以看作是抛物线的一部分(如图),其中出球点B离地面0点的距离是1m,球落地点A到0点的距离是4m,那么羽毛球到达最高点时离地面( )
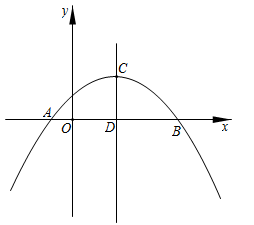
A、(32﹣2x)(20﹣x)=570 B、32x+2×20x=32×20﹣570 C、(32﹣x)(20﹣x)=32×20﹣570 D、32x+2×20x﹣2x2=5706. 学校早上8:20上第一节课,40分钟后下课,这节课中分针转动的角度为( )A、180° B、240° C、270° D、200°7. 把抛物线向左平移2个单位,再向上平移1个单位,再绕原点旋转180°所得的抛物线的解析式是( )A、 B、 C、 D、8. 在羽毛球比赛中,某次羽毛球的运动路线可以看作是抛物线的一部分(如图),其中出球点B离地面0点的距离是1m,球落地点A到0点的距离是4m,那么羽毛球到达最高点时离地面( ) A、米 B、米 C、米 D、米9. 已知抛物线 , 具有如下性质:该抛物线上任意一点到定点的距离与到x轴的距离始终相等,如图,点M的坐标为 , P是抛物线上一个动点,则当的周长最小时的值是( )
A、米 B、米 C、米 D、米9. 已知抛物线 , 具有如下性质:该抛物线上任意一点到定点的距离与到x轴的距离始终相等,如图,点M的坐标为 , P是抛物线上一个动点,则当的周长最小时的值是( ) A、 B、 C、 D、10. 抛物线 的对称轴为直线 .若关于 的一元二次方程 ( 为实数)在 的范围内有实数根,则 的取值范围是( )A、 B、 C、 D、11. 如图 ,已知△ABC 中,∠C=90°,AC=BC= , 将△ABC 绕点 A 顺时针方向旋转 60°得到△A′B′C′的位置,连接 C′B,则 C′B 的长为 ( )
A、 B、 C、 D、10. 抛物线 的对称轴为直线 .若关于 的一元二次方程 ( 为实数)在 的范围内有实数根,则 的取值范围是( )A、 B、 C、 D、11. 如图 ,已知△ABC 中,∠C=90°,AC=BC= , 将△ABC 绕点 A 顺时针方向旋转 60°得到△A′B′C′的位置,连接 C′B,则 C′B 的长为 ( ) A、2- B、 C、 D、112. 如图,抛物线与交于点 , 过点A作x轴的平行线,分别交两条抛物线于B、C两点,且D、E分别为顶点.则下列结论:①;②是等边三角形;③;④当时, , 其中正确结论的个数有( )
A、2- B、 C、 D、112. 如图,抛物线与交于点 , 过点A作x轴的平行线,分别交两条抛物线于B、C两点,且D、E分别为顶点.则下列结论:①;②是等边三角形;③;④当时, , 其中正确结论的个数有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 在直角坐标系中,点关于原点对称的点的坐标是 .14. 已知方程x2﹣10x+24=0的两个根是一个等腰三角形的两边长,则这个等腰三角形的周长为 .
15. 如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m,水面下降2m,水面宽度增加m.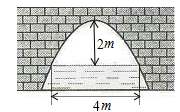 16. 一个凸多边形共有20条对角线,那么它是边形.17. 如图,正方形ABCD的边长为 , 点A与原点重合,点B在y轴的正半轴上,将正方形ABCD绕点A逆时针旋转30°至正方形位置,与CD相交于P,则直线的解析式为 .
16. 一个凸多边形共有20条对角线,那么它是边形.17. 如图,正方形ABCD的边长为 , 点A与原点重合,点B在y轴的正半轴上,将正方形ABCD绕点A逆时针旋转30°至正方形位置,与CD相交于P,则直线的解析式为 . 18. 如图,线段AB的长为1,C在AB上,D在AC上,且 , , , 则AE的长为 .
18. 如图,线段AB的长为1,C在AB上,D在AC上,且 , , , 则AE的长为 .
三、解答题
-
19.(1)、解方程: .(2)、如图,在平面直角坐标系中,的三个顶点都在格点上.
①画出绕原点顺时针旋转90°后的 .
②写出图中点和点的坐标.
 20. 已知、是方程的两实数根.(1)、求的值.(2)、求的值.21. 二次函数的图象与x轴的两交点的坐标是 , , 与y轴的交点的坐标是 .
20. 已知、是方程的两实数根.(1)、求的值.(2)、求的值.21. 二次函数的图象与x轴的两交点的坐标是 , , 与y轴的交点的坐标是 . (1)、求此二次函数的解析式.(2)、在平面直角坐标系内画出的大致图象,根据图象指出:当时,y的取值范围.22. 某商场销售某种品牌的手机,每部进货价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8部:而当销售价每降低50元时,平均每天就能多售出4部.(1)、若设每部手机降低x元,每天的销售利润为y元,试写出y与x之间的函数关系式.(2)、商场要想获得最大利润,每部手机的售价应订为多少元?此时的最大利润是多少元?
(1)、求此二次函数的解析式.(2)、在平面直角坐标系内画出的大致图象,根据图象指出:当时,y的取值范围.22. 某商场销售某种品牌的手机,每部进货价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8部:而当销售价每降低50元时,平均每天就能多售出4部.(1)、若设每部手机降低x元,每天的销售利润为y元,试写出y与x之间的函数关系式.(2)、商场要想获得最大利润,每部手机的售价应订为多少元?此时的最大利润是多少元?