四川省眉山市丹棱县2021-2022学年九年级上学期期中数学试题

试卷更新日期：2022-09-27 类型：期中考试

进入出卷网下载

一、单选题

1. 函数 $y = \frac{1}{\sqrt{x - 2}}$ 中，自变量 $x$ 的取值范围是（）

A、 $x > 2$ B、 $x \neq 2$ C、 $x$ < $2$ D、 $x \neq - 2$

查看试题解析
2. 若关于x的方程（m﹣1）x²+mx﹣1＝0是一元二次方程，则m的取值范围是（）

A、m≠1 B、m＝1 C、m≥1 D、m≠0

查看试题解析
3. 如图， $D E / / B C$ ，下列各式不正确的是（）

A、 $\frac{A D}{A B} = \frac{A E}{A C}$ B、 $\frac{A D}{B D} = \frac{A E}{C E}$ C、 $\frac{A D}{A C} = \frac{A E}{A B}$ D、 $\frac{A D}{A E} = \frac{A B}{A C}$

查看试题解析
4. 若 $x_{1} ， x_{2}$ 为一元二次方程 $3 x^{2} - 2 x - 1 = 0$ 的两个根，则 $x_{1} + x_{2} =$ （）

A、 $- \frac{2}{3}$ B、 $\frac{2}{3}$ C、 $2$ D、 $- \frac{1}{3}$

查看试题解析
5. 下列二次根式中，与 $\sqrt{3}$ 是同类二次根式的是（）

A、 $\sqrt{6}$ B、 $\sqrt{9}$ C、 $\sqrt{12}$ D、 $\sqrt{18}$

查看试题解析
6. 下列两个三角形不一定相似的是（）

A、两条直角边的比都是 $2 : 3$ 的两个直角三角形 B、腰与底的比都是 $2 : 3$ 的两个等腰三角形 C、有一个内角为 $50 °$ 的两个直角三角形 D、有一个内角为 $50 °$ 的两个等腰三角形

查看试题解析
7. 根据下列表格的对应值，判断方程ax²+bx+c=0（a≠0，a、b、c为常数）一个解的范围是（　　）
x
3.23
3.24
3.25
3.26
ax²+bx+c
﹣0.06
﹣0.02
0.03
0.09

A、3＜x＜3.23 B、3.23＜x＜3.24 C、3.24＜x＜3.25 D、3.25＜x＜3.26

查看试题解析
8. 如图，在菱形ABCD中，E为边CD上一点，连结AE并延长，交BC的延长线于点F，若CE＝1，DE＝2，则CF长为（）

A、1 B、1.5 C、2 D、2.5

查看试题解析
9. 若 $\sqrt{a^{2} - 6 a + 9} = 3 - a$ ，则（）

A、 $a > 3$ B、 $a < 3$ C、 $a \geq 3$ D、 $a \leq 3$

查看试题解析
10. 如图，△ABC与△DEF是以点O为位似中心的位似图形，且位似比为1∶2，下列结论不正确的是（）

A、AC∥DF B、 $\frac{A B}{D E} = \frac{O A}{O D} = \frac{1}{2}$ C、BC是△OEF的中位线 D、S△ABC：S△DEF =1：2

查看试题解析
11. 在一幅长80cm，宽50cm的矩形风景画的四周镶一条金色纸边，制成一幅矩形挂图，如图所示，如果要使整个挂图的面积是5400cm² ，设金色纸边的宽为xcm，那么x满足的方程是（）

A、x²+130x﹣1400＝0 B、x²+65x﹣350＝0 C、x²﹣130x﹣1400＝0 D、x²﹣65x﹣350＝0

查看试题解析
12. 如图，在△ABC中，AD、BE分别为边BC、AC上的高，AD与BE交于F，连接ED，则下列结论：①△AEF∽△BDF；②△DEF∽△BAF；③∠DEC＝∠ABC；④BD $\cdot$ DC＝DF $\cdot$ DA，其中正确的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

13. 已知 $\sqrt{x + 4} = 3$ ，则 $x =$ ．

查看试题解析
14. 如图，直线 $l_{1} / / l_{2} / / l_{3}$ ，直线 $A C$ 和 $D F$ 被 $l_{1}$ ， $l_{2}$ ， $l_{3}$ 所截， $A B = 5$ ， $B C = 6$ ， $E F = 4$ ，则 $D E$ 的长为．

查看试题解析
15. 已知 $f (x) = \frac{6}{x}$ ，那么 $f (\sqrt{3}) =$ ．

查看试题解析
16. 设 $x_{1}$ ， $x_{2}$ 是方程 $x^{2} - x - 1 = 0$ 的两个实数根，则 ${x_{1}}^{2} - x_{1} + x_{1} x_{2} =$ ．

查看试题解析
17. 若 $\frac{a}{2} = \frac{b}{3} = \frac{c}{4}$ ， $a + b + c = 18$ ，则a的值为．

查看试题解析
18. 如图，在矩形ABCD中，AB=4，BC=6，点P是线段AD上的一动点，点E是边AB的中点，当 $∠ E P C = 90$ °时，AP的长为．

查看试题解析

三、解答题

19.

(1)、计算： $| - 3 | - \sqrt{18} \times (π - 3)^{0} + \frac{1}{\sqrt{2} + 1}$

(2)、解方程： $x^{2} - 3 x - 4 = 0$

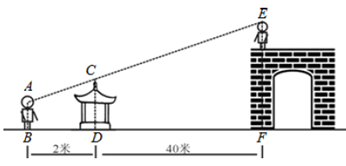
(3)、解方程： $y^{2} + 2 y = 5$

查看试题解析
20. 先化简，后求值： $\frac{x^{2} - 4 x + 4}{x^{2} - 2 x} \div (x - \frac{4}{x})$ ，其中 $x = \sqrt{3} - 2$ ．

查看试题解析
21. 《铁血红安》在中央一台热播后，吸引了众多游客前往影视基地游玩. 某天小明站在地面上给站在城楼上的小亮照相时发现：他的眼睛、凉亭顶端、小亮头顶三点恰好在一条直线上（如图）. 已知小明的眼睛离地面1. 65米，凉亭顶端离地面2米，小明到凉亭的距离为2米，凉亭离城楼底部的距离为40米，小亮身高1. 7米. 请根据以上数据求出城楼的高度.
.

查看试题解析
22. 已知关于x的一元二次方程mx²－2mx＋m－2＝0.

(1)、若方程有两个实数根，求m的取值范围；

(2)、设方程的两实根为x₁ ， x₂ ，且|x₁－x₂|＝1，求m的值．

查看试题解析
23. 如图，已知O是坐标原点，B，C两点的坐标分别为（3，﹣1），（2，1）．

(1)、以O点为位似中心在y轴的左侧将△OBC放大到两倍，画出图形；

(2)、分别写出B，C两点的对应点B′，C′的坐标；

(3)、求△OB′C′的面积．

查看试题解析
24. 如图，在 $Δ A B C$ 中， $A D$ 是 $Δ A B C$ 的中线， $E$ 是 $A D$ 上一点，且 $C E = C D$ ， $∠ D A C = ∠ B$ .求证：

(1)、 $Δ A E C$ ∽ $Δ B D A$ ；

(2)、 $C D^{2} = A D \cdot A E$ ．

查看试题解析
25. 某商场一种商品的进价为每件30元，售价为每件40元．每天可销售48件，为尽快减少库存，商场决定降价促销．

(1)、若该商品连续两次下调相同的百分率后售价降至每件32.4元，求每次降价的百分率；

(2)、经调查，若该商品每降价1元，每天可多销售8件，那么每天要想获得510元的利润且尽快减少库存，每件应降价多少元？

查看试题解析
26. 如图，在等腰直角三角形 ABC 中，∠ACB=90°，AC=BC= $2 \sqrt{5}$ ，边长为 2 的正方形 DEFG 的对角线交点与点 C 重合，连接 AD，BE．

(1)、求证：△ACD≌△BCE；

(2)、当点 D 在△ABC 内部，且∠ADC=90°时，设 AC 与 DG 相交于点 M，求 AM 的长；

(3)、将正方形DEFG绕点 C 旋转一周，当点A、D、E三点在同一直线上时，求AD的长．

查看试题解析

x	3.23	3.24	3.25	3.26
ax²+bx+c	﹣0.06	﹣0.02	0.03	0.09