四川省乐山市市中区2021-2022学年九年级上学期期中数学试题
试卷更新日期:2022-09-27 类型:期中考试
一、单选题
-
1. 下列计算正确的是( )A、 B、 C、 D、2. 若代数式有意义,则x的取值范围是( )A、 B、 C、 D、3. 若3a-2b=0,则 的值为( )A、 B、 C、1 D、4. 已知一元二次方程 有一个根为3,则 的值为( )A、2 B、 C、4 D、5. 如图,在长为32米、宽为12米的矩形地面上修建如图所示的道路(图中的阴影部分)余下部分铺设草坪,要使得草坪的面积为300平方米,则可列方程为( )
 A、 B、 C、 D、6. 如图,在中, , 、三等分 , D、E在边上,则其中的相似三角形有( )
A、 B、 C、 D、6. 如图,在中, , 、三等分 , D、E在边上,则其中的相似三角形有( ) A、1对 B、2对 C、3对 D、6对7. 如图,在的边上任取两点B,C,过B作的平行线交于N,过N作的平行线交于D.若 , 则的值为( ).
A、1对 B、2对 C、3对 D、6对7. 如图,在的边上任取两点B,C,过B作的平行线交于N,过N作的平行线交于D.若 , 则的值为( ). A、 B、 C、2 D、38. 如图所示,直线y=x﹣1与x轴交于A,与y 轴交于B,在第一象限内找点C,使△AOC与△AOB相似,则共能找到的点C的个数( )
A、 B、 C、2 D、38. 如图所示,直线y=x﹣1与x轴交于A,与y 轴交于B,在第一象限内找点C,使△AOC与△AOB相似,则共能找到的点C的个数( ) A、1 B、2 C、3 D、49. 小刚在解关于 的方程 时,只抄对了 , ,解出其中一个根是 .他核对时发现所抄的b比原方程的b值小1,则原方程的根的情况是( )A、不存在实数根 B、有两个不相等的实数根 C、有另一个根是 D、有两个相等的实数根10. 如图,在中, , , , 且 , 若 , 点是线段上的动点,则的最小值是( )
A、1 B、2 C、3 D、49. 小刚在解关于 的方程 时,只抄对了 , ,解出其中一个根是 .他核对时发现所抄的b比原方程的b值小1,则原方程的根的情况是( )A、不存在实数根 B、有两个不相等的实数根 C、有另一个根是 D、有两个相等的实数根10. 如图,在中, , , , 且 , 若 , 点是线段上的动点,则的最小值是( )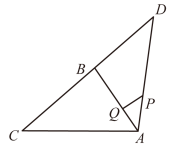 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 化简:=12. 已知a,b都是实数, , 则代数式的值为 .13. 已知x2+6x=﹣1可以配成(x+p)2=q的形式,则q=.14. 如图,在矩形ABCD中,点E,F分别是AD,BC边的中点,连接EF,若矩形ABFE与矩形ABCD相似, , 则矩形ABCD的面积为 .
 15. 已知α,β是方程x2﹣4x﹣5=0的两个实数根,则α2﹣2αβ﹣4α的值为.16. 如图, , , , 在中截出一个正方形 , 使点 , 分别在AC,BC边上,边在AB边上;在在截出第二个正方形 , 使点 , 分别在 , 边上,边在边上; , 依此方法作下去,则:
15. 已知α,β是方程x2﹣4x﹣5=0的两个实数根,则α2﹣2αβ﹣4α的值为.16. 如图, , , , 在中截出一个正方形 , 使点 , 分别在AC,BC边上,边在AB边上;在在截出第二个正方形 , 使点 , 分别在 , 边上,边在边上; , 依此方法作下去,则: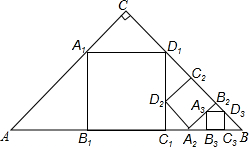 (1)、正方形的边长为;(2)、第n个正方形的边长为 .
(1)、正方形的边长为;(2)、第n个正方形的边长为 .三、解答题
-
17. 解下列方程:(1)、;(2)、 .18. 计算: .19. 如图,已知 , 求证: .
 20. 已知一本数学书长为 , 宽为 , 厚为 . 一张长方形包书纸如图所示,它的面积为 , 虚线表示的是折痕.由长方形相邻两边与折痕围成的四角均为大小相同的正方形,求正方形的边长.
20. 已知一本数学书长为 , 宽为 , 厚为 . 一张长方形包书纸如图所示,它的面积为 , 虚线表示的是折痕.由长方形相邻两边与折痕围成的四角均为大小相同的正方形,求正方形的边长. 21. 已知 .(1)、求的值;(2)、化简并求值: .22. 如图,在正方形ABCD中,点G是对角线上一点,CG的延长线交AB于点E,交DA的延长线于点F,连接AG.
21. 已知 .(1)、求的值;(2)、化简并求值: .22. 如图,在正方形ABCD中,点G是对角线上一点,CG的延长线交AB于点E,交DA的延长线于点F,连接AG. (1)、求证:AG=CG;(2)、若GE•GF=9,求CG的长.23. 已知关于x的一元二次方程.(1)、求证:不论k取何值,此一元二次方程总有两个不相等的实数根;(2)、若此一元二次方程的两根是两直角边AB、AC的长,斜边BC的长为10,求k的值.24. 随着疫情在国内趋稳,却在国外迎来爆发期,多国采购中国防疫物资需求大增.某工厂建了1条口罩生产线生产口罩,开工第一天生产300万个,第三天生产432万个,若每天生产口罩的个数增长的百分率相同,请解答下列问题:(1)、每天增长的百分率是多少?(2)、经过一段时间后,工厂发现1条生产线最大产能是900万个/天,但如果每增加1条生产线,由于资源调配等原因每条生产线的最大产能将减少30万个/天,现该厂要保证每天生产口罩3900万个,应该建几条生产线?25. 如图(1),在四边形ABCD中,AB∥DC,CB⊥AB,AB=16cm,BC=6cm,CD=8cm,动点P从点D开始沿DA边匀速运动,动点Q从点A开始沿AB边匀速运动,它们的运动速度均为2cm/s.点P和点Q同时出发,设运动的时间为t(s),0<t<5
(1)、求证:AG=CG;(2)、若GE•GF=9,求CG的长.23. 已知关于x的一元二次方程.(1)、求证:不论k取何值,此一元二次方程总有两个不相等的实数根;(2)、若此一元二次方程的两根是两直角边AB、AC的长,斜边BC的长为10,求k的值.24. 随着疫情在国内趋稳,却在国外迎来爆发期,多国采购中国防疫物资需求大增.某工厂建了1条口罩生产线生产口罩,开工第一天生产300万个,第三天生产432万个,若每天生产口罩的个数增长的百分率相同,请解答下列问题:(1)、每天增长的百分率是多少?(2)、经过一段时间后,工厂发现1条生产线最大产能是900万个/天,但如果每增加1条生产线,由于资源调配等原因每条生产线的最大产能将减少30万个/天,现该厂要保证每天生产口罩3900万个,应该建几条生产线?25. 如图(1),在四边形ABCD中,AB∥DC,CB⊥AB,AB=16cm,BC=6cm,CD=8cm,动点P从点D开始沿DA边匀速运动,动点Q从点A开始沿AB边匀速运动,它们的运动速度均为2cm/s.点P和点Q同时出发,设运动的时间为t(s),0<t<5 (1)、用含t的代数式表示AP;(2)、当以点A、P、Q为顶点的三角形与△ABD相似时,求t的值;(3)、如图(2),延长QP、BD,两延长线相交于点M,当△QMB为直角三角形时,求t的值.26. 数学课上,有这样一道探究题.
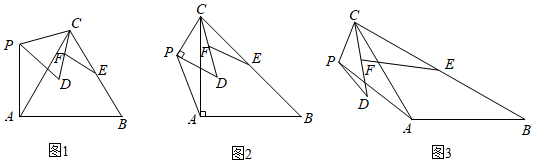
(1)、用含t的代数式表示AP;(2)、当以点A、P、Q为顶点的三角形与△ABD相似时,求t的值;(3)、如图(2),延长QP、BD,两延长线相交于点M,当△QMB为直角三角形时,求t的值.26. 数学课上,有这样一道探究题.如图,已知中,AB=AC=m,BC=n, , 点P为平面内不与点A、C重合的任意一点,将线段CP绕点P顺时针旋转a,得线段PD,E、F分别是CB、CD的中点,设直线AP与直线EF相交所成的较小角为β,探究的值和的度数与m、n、α的关系,请你参与学习小组的探究过程,并完成以下任务:
 (1)、填空:
(1)、填空:【问题发现】
小明研究了时,如图1,求出了 ▲ , ▲ ;
小红研究了时,如图2,求出了 ▲ , ▲ ;
【类比探究】
他们又共同研究了α=120°时,如图3,也求出了;
【归纳总结】
最后他们终于共同探究得出规律: ▲ (用含m、n的式子表示); ▲ (用含α的式子表示).
(2)、求出时的值和的度数.