人教版九年级上对接中考知识点复习专项计划——弧长与扇形面积
试卷更新日期:2022-09-27 类型:复习试卷
一、单选题
-
1. 如图,PA、PB是⊙O的切线,切点是A、B,已知∠P=60°,OA=3,那么∠AOB所对弧的长度为( )
 A、6π B、5π C、3π D、2π2. 如图,已知扇形OAB的半径OA=6,点P为弧AB上一动点,过点P作PC⊥OA,PD⊥OB,连结CD,当CD取得最大值时,扇形OAB的面积为( )
A、6π B、5π C、3π D、2π2. 如图,已知扇形OAB的半径OA=6,点P为弧AB上一动点,过点P作PC⊥OA,PD⊥OB,连结CD,当CD取得最大值时,扇形OAB的面积为( )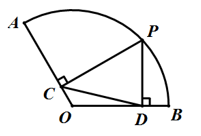 A、 B、 C、 D、3. 如图,已知PA与⊙O相切于点A,点B为⊙上一点,∠AOB=120°,过点B作BC⊥PA于点C,BC交⊙O于点D,连接AB.已知OA=2,则图中阴影部分的面积是( )
A、 B、 C、 D、3. 如图,已知PA与⊙O相切于点A,点B为⊙上一点,∠AOB=120°,过点B作BC⊥PA于点C,BC交⊙O于点D,连接AB.已知OA=2,则图中阴影部分的面积是( )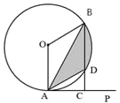 A、 B、 C、π D、4. 如图,在圆中半径OC弦AB,且弦AB=CO=2,则图中阴影部分面积为( )
A、 B、 C、π D、4. 如图,在圆中半径OC弦AB,且弦AB=CO=2,则图中阴影部分面积为( ) A、 B、 C、 D、5. 如图所示,以AB为直径的半圆,绕点B顺时针旋转60°,点A旋转到点A′,且AB=4,则图中阴影部分的面积是( )
A、 B、 C、 D、5. 如图所示,以AB为直径的半圆,绕点B顺时针旋转60°,点A旋转到点A′,且AB=4,则图中阴影部分的面积是( ) A、 B、 C、8 D、6. 如图,菱形 中, , .以A为圆心, 长为半径画 ,点P为菱形内一点,连 , , .若 ,且 ,则图中阴影部分的面积为( )
A、 B、 C、8 D、6. 如图,菱形 中, , .以A为圆心, 长为半径画 ,点P为菱形内一点,连 , , .若 ,且 ,则图中阴影部分的面积为( )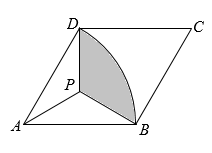 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 如图,在ΔABC中,∠ACB=90°,D是BC边上的点,CD=2,以CD为直径的⨀O与AB相切于点E.若弧DE的长为 则阴影部分的面积.(保留π)
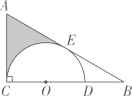 8. 如图,是的直径,弦 , 垂足为 , , , 则 .
8. 如图,是的直径,弦 , 垂足为 , , , 则 . 9. 如图,是的直径,点在上, , , . 若的半径为1,则图中阴影部分的面积是(结果保留).
9. 如图,是的直径,点在上, , , . 若的半径为1,则图中阴影部分的面积是(结果保留). 10. 如图,△ABC各边长都大于4,⊙A、⊙B、⊙C的半径都等于2,则图中三个阴影部分的面积之和为 (结果保留π) ;
10. 如图,△ABC各边长都大于4,⊙A、⊙B、⊙C的半径都等于2,则图中三个阴影部分的面积之和为 (结果保留π) ;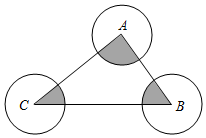 11. 如图,等边 的边长为1,以 为圆心, 为半径画弧,交 的延长线于 , 再以 为圆心, 为半径画弧,交 的延长线于 , 再以 为圆心, 为半径画强,交 的延长线于 , 则由弧 , 弧 , 优弧 及线段 围成的图形( )的周长为 .
11. 如图,等边 的边长为1,以 为圆心, 为半径画弧,交 的延长线于 , 再以 为圆心, 为半径画弧,交 的延长线于 , 再以 为圆心, 为半径画强,交 的延长线于 , 则由弧 , 弧 , 优弧 及线段 围成的图形( )的周长为 .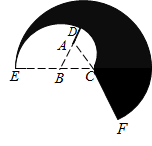 12. 如图,扇形AOB,正方形OCDE的顶点C,E,D,分别在OA,OB,弧AB上,过点A作 , 交ED的延长线于点F.若图中阴影部分的面积为 , 则扇形AOB的半径为.
12. 如图,扇形AOB,正方形OCDE的顶点C,E,D,分别在OA,OB,弧AB上,过点A作 , 交ED的延长线于点F.若图中阴影部分的面积为 , 则扇形AOB的半径为. 13. 一条弧所对的圆心角为 , 弧长等于 , 则这条弧的半径为 .14. 如图,点A,B,C在⊙O上,四边形OABC是平行四边形,若对角线AC=2 , 则的长为 .
13. 一条弧所对的圆心角为 , 弧长等于 , 则这条弧的半径为 .14. 如图,点A,B,C在⊙O上,四边形OABC是平行四边形,若对角线AC=2 , 则的长为 . 15. 如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°.把△ABC绕点A按顺时针方向旋转60°后得到△AB′C′,若AB=4,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是 . (结果保留π).
15. 如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°.把△ABC绕点A按顺时针方向旋转60°后得到△AB′C′,若AB=4,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是 . (结果保留π).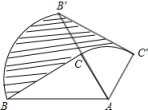 16. 如图Rt△ABC,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”:当AC=6,BC=8时,则阴影部分的面积为 .
16. 如图Rt△ABC,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”:当AC=6,BC=8时,则阴影部分的面积为 .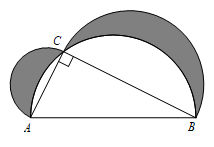 17. 如图,半径为 2 的⊙O 与正六边形 ABCDEF 相切于点 C,F,则图中阴影部分的面积为.
17. 如图,半径为 2 的⊙O 与正六边形 ABCDEF 相切于点 C,F,则图中阴影部分的面积为.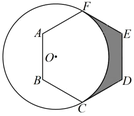
三、综合题
-
18. 在古代,智慧的劳动人民已经会使用“石磨”,其原理为在磨盘的边缘连接一个固定长度的“杠杆”,推动“杠杆”带动磨盘转动,将粮食磨碎.如图,为圆的直径,是的一条弦,为弧的中点,作于点 , 交的延长线于点 , 连接 .
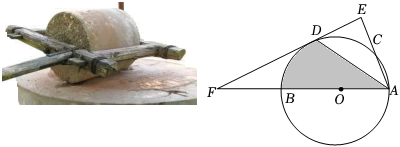 (1)、若 , 则圆心到“杠杆”的距离是多少?说明你的理由;(2)、若 , 求阴影部分的面积.结果保留19. 如图,在Rt ABC中,∠C=90°,点D在AB上,以AD为直径的⊙O与BC相交于点E,与AC相交于点F,AE平分∠BAC.
(1)、若 , 则圆心到“杠杆”的距离是多少?说明你的理由;(2)、若 , 求阴影部分的面积.结果保留19. 如图,在Rt ABC中,∠C=90°,点D在AB上,以AD为直径的⊙O与BC相交于点E,与AC相交于点F,AE平分∠BAC.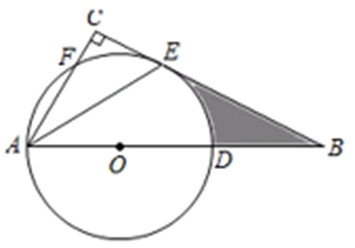 (1)、求证:BC是⊙O的切线.(2)、若∠EAB=30°,OD=5,求图中阴影部分的周长.20. 如图,有一个点O和△ABC,
(1)、求证:BC是⊙O的切线.(2)、若∠EAB=30°,OD=5,求图中阴影部分的周长.20. 如图,有一个点O和△ABC, (1)、分别画出△ABC绕点O逆时针旋转90°和180°后的图形.(2)、若OB长度为4,求出△ABC绕点O逆时针旋转90°时点B旋转到对应点的路径长度(结果保留π).21. 如图,AB是⊙O的弦,过点O作OC⊥OA,OC交AB于P,CP=BC,点Q是上的一点.
(1)、分别画出△ABC绕点O逆时针旋转90°和180°后的图形.(2)、若OB长度为4,求出△ABC绕点O逆时针旋转90°时点B旋转到对应点的路径长度(结果保留π).21. 如图,AB是⊙O的弦,过点O作OC⊥OA,OC交AB于P,CP=BC,点Q是上的一点.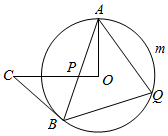 (1)、求证:BC是⊙O的切线;(2)、已知∠BAO=25°,求∠AQB的度数;(3)、在(2)的条件下,若OA=18,求的长.22. 如图,已知为的直径,切于点C,交的延长线于点D,且 .
(1)、求证:BC是⊙O的切线;(2)、已知∠BAO=25°,求∠AQB的度数;(3)、在(2)的条件下,若OA=18,求的长.22. 如图,已知为的直径,切于点C,交的延长线于点D,且 . (1)、求的大小;(2)、若 , 求的长.23. 如图,是⊙的直径,弦 , 垂足为E,弦与弦相交于点G,且 , 过点C作的垂线交的延长线于点H.
(1)、求的大小;(2)、若 , 求的长.23. 如图,是⊙的直径,弦 , 垂足为E,弦与弦相交于点G,且 , 过点C作的垂线交的延长线于点H. (1)、判断与⊙的位置关系并说明理由;(2)、若 , 求弧的长.24. 如图, 是 的直径, 是圆上两点,且有 ,连结 ,作 的延长线于点E.
(1)、判断与⊙的位置关系并说明理由;(2)、若 , 求弧的长.24. 如图, 是 的直径, 是圆上两点,且有 ,连结 ,作 的延长线于点E. (1)、求证: 是 的切线;(2)、若 ,求阴影部分的面积.(结果保留 )25. 如图, 内接于 ,且 ,P是 上一点,且 .
(1)、求证: 是 的切线;(2)、若 ,求阴影部分的面积.(结果保留 )25. 如图, 内接于 ,且 ,P是 上一点,且 .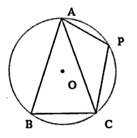 (1)、求 的度数;(2)、若 的半径为6,求 的长(结果保留 ).26. 如图,在△ABC中,AB=AC,∠BAC=54°,以AB为直径的⊙O分别交AC,BC 于点D,E,过点B作⊙O的切线,交AC的延长线于点F.
(1)、求 的度数;(2)、若 的半径为6,求 的长(结果保留 ).26. 如图,在△ABC中,AB=AC,∠BAC=54°,以AB为直径的⊙O分别交AC,BC 于点D,E,过点B作⊙O的切线,交AC的延长线于点F. (1)、求证:BE=CE;(2)、求∠CBF的度数;(3)、若AB=6,求的长.
(1)、求证:BE=CE;(2)、求∠CBF的度数;(3)、若AB=6,求的长.

