四川省宜宾市兴文县2021-2022学年八年级上学期期中数学试题

试卷更新日期：2022-09-27 类型：期中考试

进入出卷网下载

一、单选题

1. $\sqrt{5}$ 的相反数是（）

A、 $\sqrt{5}$ B、 $- \sqrt{5}$ C、 $| \sqrt{5} |$ D、 $| - \sqrt{5} |$

查看试题解析
2. 下列实数中，是无理数的是（）

A、-7 B、 $\frac{5}{3}$ C、 $- 5 π$ D、 $\sqrt[3]{8}$

查看试题解析
3. 下列运算正确的是（）

A、 $a^{3} \cdot a^{3} = 2 a^{3}$ B、 $a^{12} ÷ a^{3} = a^{4}$ C、 ${(a^{5})}^{2} = a^{10}$ D、 $(- 2 a)^{2} = - 4 a^{2}$

查看试题解析
4. 下列命题中，是真命题的是（）

A、同位角相等 B、有理数和数轴上的点一一对应 C、三角形的一个外角大于任何一个内角 D、全等三角形对应边上的中线相等

查看试题解析
5. 下列从左边到右边的变形中，是因式分解的是（）

A、 $a^{2} - 9 = (a - 3) (a + 3)$ B、 ${(x - y)}^{2} = x^{2} - y^{2}$ C、 $x^{2} - 4 + 4 x = (x + 2) (x - 2) + 4 x$ D、 $x^{2} + 3 x + 1 = x (x + 3 + \frac{1}{x})$

查看试题解析
6. 如图，直线EF经过AC的中点O，交AB于点E，交CD于点F，下列不能使△AOE≌△COF的条件为（）

A、∠A＝∠C B、AB∥CD C、AE＝CF D、OE＝OF

查看试题解析
7. 估计 $\sqrt{7}$ +1的值在（）

A、2到3之间 B、3到4之间 C、4到5之间 D、5到6之间

查看试题解析
8. 若要使 $4 x^{2} + m x + \frac{1}{64}$ 成为一个两数和（差）的平方，则 $m$ 的值应为（）

A、 $\pm \frac{1}{2}$ B、 $- \frac{1}{2}$ C、 $\pm \frac{1}{4}$ D、 $- \frac{1}{4}$

查看试题解析
9. 如图， $A B$ ， $C D$ 相交于点 $E$ ，若 $△ A B C ≅ △ A D E$ ， $∠ B A C = 28 °$ ，则 $∠ B$ 的度数是（）

A、 $28 °$ B、 $38 °$ C、 $45 °$ D、 $48 °$

查看试题解析
10. 下列说法：①9的平方根是 $\pm$ 3；②整式乘法与因式分解过程互逆；③2是 $\sqrt[3]{8}$ 的算术平方根；④“周长相等的两个三角形全等”是假命题；⑤两角分别相等且一组边对应相等不一定能判定两个三角形全等．其中正确说法的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
11. 如图，有10个形状大小一样的小长方形①，将其中的3个小长方形①放入正方形②中，剩余的7个小长方形①放入长方形③中，其中正方形②中的阴影部分面积为22，长方形③中的阴影部分面积为96，那么一个小长方形①的面积为（）

A、5 B、6 C、9 D、10

查看试题解析
12. 在如图所示的 6×6 网格中，△ABC是格点三角形（即顶点恰好是网格线的交点），则与△ABC有一条公共边且全等（不含△ABC）的所有格点三角形的个数（）

A、3 个 B、4 个 C、6 个 D、7 个

查看试题解析

二、填空题

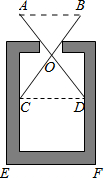
13. 把命题“直角三角形的两个锐角互余”改写成“如果……那么……”的形式：.

查看试题解析
14. 比较大小： $\sqrt[3]{3}$ $| - \sqrt{3} |$ （填“ $>$ ”或“ $<$ ”）

查看试题解析
15. 在测量一个小口圆形容器的壁厚时，小明用“ $X$ 型转动钳”按如图所示的方法进行测量，其中OA=OD，OB=OC，测得AB=7厘米，EF=9厘米，则圆形容器的壁厚是厘米．

查看试题解析
16. 一个正数的两个平方根分别是 $a + 4$ 和 $- 7 - b$ ，且 $a b = - \frac{1}{2}$ ，则 $a^{2} + b^{2}$ 的值是．

查看试题解析
17. 若 $(x - 3) (x^{2} + 2 m x - n)$ 的乘积展开式中不含 $x^{2}$ 和 $x$ 项，则 $m + n$ 的值为．

查看试题解析
18. 如图，直线PQ经过Rt△ABC的直角顶点C，△ABC的边上有两个动点D、E，点D以1cm/s的速度从点A出发，沿AC→CB移动到点B，点E以3cm/s的速度从点B出发，沿BC→CA移动到点A，两动点中有一个点到达终点后另一个点继续移动到终点．过点D、E分别作DM⊥PQ，EN⊥PQ，垂足分别为点M、N，若AC=6cm，BC=8cm，设运动时间为t，则当t= s时，以点D、M、C为顶点的三角形与以点E、N、C为顶点的三角形全等．

查看试题解析

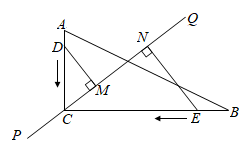
三、解答题

19.

(1)、计算： $\frac{1}{\sqrt[3]{27}} \times 9 + {(- \sqrt{4})}^{2} - | 5 - \sqrt{3} |$ ；

(2)、求 $x$ 的值： $- \frac{1}{64} {(x - 3)}^{3} = 1$ ．

查看试题解析
20. 如图，在 $△ A B C$ 和 $△ D E F$ 中，边 $A C$ ， $D E$ 相交于点 $H$ ， $A B ∥ D E$ ， $A B = D E$ ， $B E = C F$ ．

(1)、求证： $△ A B C ≅ △ D E F$ ；

(2)、若 $∠ B = 55 °$ ， $∠ F = 100 °$ ，求 $∠ C H E$ 的度数．

查看试题解析
21. 把下列多项式分解因式：

(1)、 $m^{4} - 1$ ；

(2)、 $3 a {(a - 1)}^{2} - 18 a (a - 1) + 27 a$ ．

查看试题解析
22. 先化简，再求值：

(1)、 $2 y {(y^{2})}^{3} - {(2 y^{3})}^{3} \div 2 y^{2}$ ，其中 $y = 1$ ；

(2)、 $[{(x - y)}^{2} + (2 x - y) (2 x + y) - 2 (2 x^{2} + x y)] \div (- x)$ ，其中 $x = - \sqrt{9}$ ， $y = 4$ ．

查看试题解析
23. 小明与爸爸妈妈在公园里荡秋千，如图，小明坐在秋千的起始位置A处，OA与地面垂直，两脚在地面上用力一蹬，妈妈在距地面1.2m高的B处接住他后用力一推，爸爸在C处接住他，若妈妈与爸爸到OA的水平距离BD、CE分别为1.6m和2m，∠BOC＝90°．

(1)、△OBD与△COE全等吗？请说明理由；

(2)、爸爸是在距离地面多高的地方接住小明的？

查看试题解析
24. 【阅读】代数中的很多等式可以用几何图形直观表示，这种思想叫“数形结合”思想．如图1，现有正方形 $A$ 类、 $B$ 类卡片和长方形 $C$ 类卡片若干张，若要拼成一个长为 $2 a + b$ 、宽为 $a + 2 b$ 的大长方形，可以先计算大长方形面积为 $(2 a + b) (a + 2 b) = 2 a^{2} + 2 b^{2} + 5 a b$ ，则分别需要 $A$ 类、 $B$ 类、 $C$ 类卡片2张、2张、5张，拼成的图形如图2所示．

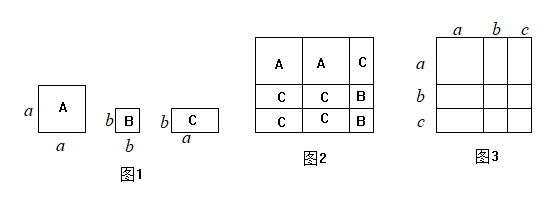(1)、【探究】若要拼成一个长为 $a + 3 b$ 、宽为 $a + b$ 的大长方形，则需要 $A$ 类、 $B$ 类、 $C$ 类卡片各多少张？并画出示意图．

(2)、【应用】①由图3可得等式：____________________；
②已知 $a + b + c = 11$ ， $a b + b c + a c = 38$ ，利用①中所得结论，求 $a^{2} + b^{2} + c^{2}$ 的值．

查看试题解析
25. 已知四边形ABCD中，AB⊥AD，BC⊥CD，AB=BC，∠ABC=120°，∠MBN=60°，∠MBN绕B点旋转，它的两边分别交AD，DC（或它们的延长线）于E，F．

(1)、如图1，当∠MBN绕B点旋转到AE=CF时，求证：AE+CF=EF．

(2)、如图2，当∠MBN绕B点旋转到AE≠CF时，上述结论是否成立？若成立，请给予证明；若不成立，线段AE，CF，EF又有怎样的数量关系？请写出你的猜想，并证明．

(3)、当∠MBN绕B点继续旋转到图3位置时，AE=10，CF=2．求EF的长度．

查看试题解析