四川省攀枝花市西区2021-2022学年八年级上学期期中数学试题
试卷更新日期:2022-09-27 类型:期中考试
一、单选题
-
1. 下列说法正确的是( )A、1的立方根是±1 B、 =±2 C、 的平方根是±3 D、0没有平方根2. 在3.14, , , , , , , 中,无理数有( )A、1个 B、2个 C、3个 D、4个3. 估算+3的值( )
A、在5和6之间 B、在6和7之间 C、在7和8之间 D、在8和9之间4. 下列计算正确的是( )A、 B、 C、 D、5. 下列多项式相乘,结果为 的是( )A、(a-2)(a-8) B、(a+2)(a-8) C、(a-2)(a+8) D、(a+2)(a+8)6. 若是一个完全平方式,则a值为( )A、-9 B、-9或11 C、9或-11 D、117. 下列由左边到右边的变形,属于因式分解的是( ).A、(x+1)(x-1)=x2-1 B、x2-2x+1=x(x-2)+1 C、a2-b2=(a+b)(a-b) D、mx+my+nx+ny=m(x+y)+n(x+y)8. 下列命题正确的是( )A、相等的角是对顶角 B、两条直线被第三条直线所截,同位角相等 C、在同一平面内,垂直于一条直线的两条直线平行 D、同旁内角互补9. 已知 则 的值是( )A、4 B、3 C、2 D、110.如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )
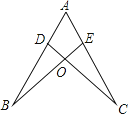 A、∠B=∠C B、AD=AE C、BD=CE D、BE=CD11. 如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1 , P2 , P3 , P4四个点中找出符合条件的点P,则点P有( )
A、∠B=∠C B、AD=AE C、BD=CE D、BE=CD11. 如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1 , P2 , P3 , P4四个点中找出符合条件的点P,则点P有( ) A、1个 B、2个 C、3个 D、4个12. 观察下列一组图形中点的个数,其中第一个图形中共有4个点,第2个图形中共有10个点,第3个图形中共有19个点,…按此规律第6个图形中共有点的个数是( )
A、1个 B、2个 C、3个 D、4个12. 观察下列一组图形中点的个数,其中第一个图形中共有4个点,第2个图形中共有10个点,第3个图形中共有19个点,…按此规律第6个图形中共有点的个数是( ) A、38 B、46 C、61 D、64
A、38 B、46 C、61 D、64二、填空题
-
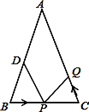
13. 若 ,则x= .14. 若 ,则 .15. 已知 , , 则的值为 .16. 如图,在△ABC中,AB=AC=24厘米,∠B=∠C ,BC=16厘米,点D为AB的中点,点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为厘米/秒时,能够在某一时刻使△BPD与△CQP全等.
三、解答题
-
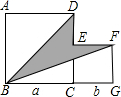
17. 计算(1)、(2)、18. 计算(1)、(16x-8x+4x)÷(-2x)(2)、19. 因式分解(1)、(2)、(x-1)(x-3)-820. 已知、满足2|-2012|=2--1 .求的值.21. 如图,两个正方形边长分别为a、b,如果a+b=17,ab=60,求阴影部分的面积.
 22. 四边形中, , 于 , 于 , CB=CD.
22. 四边形中, , 于 , 于 , CB=CD. (1)、求证:;(2)、若 , , 求的长.23. 若 x 满足 (9−x)(x−4)=4, 求 (4−x)2+(x−9)2 的值.
(1)、求证:;(2)、若 , , 求的长.23. 若 x 满足 (9−x)(x−4)=4, 求 (4−x)2+(x−9)2 的值.设 9−x=a,x−4=b, 则 (9−x)(x−4)=ab=4,a+b=(9−x)+(x−4)=5 ,
∴(9−x)2+(x−4)2=a2+b2=(a+b)2−2ab=52−2×4=13
请仿照上面的方法求解下面问题:
 (1)、若x满足 (5−x)(x−2)=2, 求 (5−x)2+(x−2)2 的值(2)、已知正方形 ABCD 的边长为x,E,F分别是AD、DC上的点,且AE=1,CF=3 ,长方形 EMFD 的面积是 48 ,分别以 MF 、 DF 作正方形,求阴影部分的面积.24. 小孟同学将等腰直角三角板()的直角顶点放在一直线上,将三角板绕点旋转,分别过 , 两点向这条直线作垂线 , , 垂足为 , .
(1)、若x满足 (5−x)(x−2)=2, 求 (5−x)2+(x−2)2 的值(2)、已知正方形 ABCD 的边长为x,E,F分别是AD、DC上的点,且AE=1,CF=3 ,长方形 EMFD 的面积是 48 ,分别以 MF 、 DF 作正方形,求阴影部分的面积.24. 小孟同学将等腰直角三角板()的直角顶点放在一直线上,将三角板绕点旋转,分别过 , 两点向这条直线作垂线 , , 垂足为 , . (1)、如图1,当点 , 都在直线上方时,猜想 , , 的数量关系是;(2)、将三角板绕点按逆时针方向旋转至图2的位置时,点在直线上方,点在直线下方.(1)中的结论成立吗?请你写出 , , 的数量关系,并证明你的结论.(3)、将三角板继续绕点逆时针旋转,当点在直线的下方,点在直线的上方时,请你画出示意图,按题意标好字母,直接写出 , , 的数量关系结论.
(1)、如图1,当点 , 都在直线上方时,猜想 , , 的数量关系是;(2)、将三角板绕点按逆时针方向旋转至图2的位置时,点在直线上方,点在直线下方.(1)中的结论成立吗?请你写出 , , 的数量关系,并证明你的结论.(3)、将三角板继续绕点逆时针旋转,当点在直线的下方,点在直线的上方时,请你画出示意图,按题意标好字母,直接写出 , , 的数量关系结论.