四川省南充市营山县2021-2022学年八年级上学期期中数学试题

试卷更新日期：2022-09-27 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列每组数分别是三根木棒的长度，能用它们首尾相连摆成一个三角形的是（）

A、3cm，4cm，8cm B、8cm，7cm，15cm C、5cm，5cm，11cm D、13cm，12cm，20cm

查看试题解析
3. 已知正 $n$ 边形的每一个内角都是144°，则 $n$ 的值是（）

A、12 B、10 C、8 D、6

查看试题解析
4. 在平面直角坐标系xOy中，点P（2，1）关于y轴对称的点的坐标是（）

A、（﹣2，1） B、（2，1） C、（﹣2，﹣1） D、（2，﹣1）

查看试题解析
5. 如图，△ABC中，AE是∠BAC的角平分线，AD是BC边上的高线，且∠B=40°，∠C=70°，则∠EAD的度数（）

A、35° B、5° C、15° D、25°

查看试题解析
6. 如图，在△ABC中，CD是AB边上的高，BE平分∠ABC，交CD于点E，BC=6，DE=3，则△BCE的面积是（）

A、9 B、7 C、10 D、18

查看试题解析
7. 如图，AF=CD，BC=EF，若要添加一个条件，使△ABC≌△DEF，可以添加（）

A、AC=DF B、∠B=∠E C、EF∥BC D、AB∥DE

查看试题解析
8. 在△ABC中，AB=5，AC=7，AD是BC边上的中线，则AD的长度的取值范围是（）

A、2＜AD＜12 B、1＜AD＜6 C、5＜AD＜7 D、 $\frac{1}{2}$ ＜AD＜3

查看试题解析
9. 如图，在 $△ A B C$ 中，点 $E$ 和 $F$ 分别是 $A C$ 、 $B C$ 上一点， $E F / / A B$ ， $∠ B C A$ 的平分线交 $A B$ 于点 $D$ ， $∠ M A C$ 是 $△ A B C$ 的外角，若 $∠ M A C = α$ ， $∠ E F C = β$ ， $∠ A D C = γ$ ，则 $α$ ， $β$ ， $γ$ 三者间的数量关系是（）

A、 $β = α + γ$ B、 $β = 2 γ - α$ C、 $β = α + 2 γ$ D、 $β = 2 α - 2 γ$

查看试题解析
10. 如图，在△ABC中，∠BAC＝90°，AD是BC边上的高，BE是AC边的中线，CF是∠ACB的角平分线，CF交AD于点G，交BE于点H，下面说法正确的是（）
①△ABE的面积＝△BCE的面积；②∠FAG＝∠FCB；③AF＝AG；④BH＝CH．

A、①②③④ B、①②③ C、②④ D、①③

查看试题解析

二、填空题

11. 如图，木工师傅做完窗框后，常像图中那样钉上一条斜拉的木条，这样做的数学原理是利用三角形的．

查看试题解析
12. 如图，在△ABC中，∠BAC=60°，BD、CE分别平分∠ABC、∠ACB，BD、CE相交于点O，则∠BOC的度数是．

查看试题解析
13. 如图，△ABC≌△ADE，若∠BAE＝135°，∠DAC＝55°，那么∠CFE的度数是．

查看试题解析
14. 如图， $∠ A = 75 °$ ， $∠ B = 65 °$ ，将纸片的一角折叠，使点 $C$ 落在 $Δ A B C$ 内部，若∠1=45°，则 $∠ 2$ = ．

查看试题解析
15. 已知a，b，c是 $△ A B C$ 的三条边长，化简 $| a + b - c | + | a - b - c |$ 的结果为．

查看试题解析
16. 如图，△ABC中，AD、BD、CD分别平分△ABC的外角∠CAE、内角∠ABC、外角∠ACF，AD∥BC．以下结论：①∠ABC=∠ACB；②∠ADC+∠ABD=90°；③BD平分∠ADC；④2∠BDC=∠BAC．其中正确的结论有．（填序号）

查看试题解析

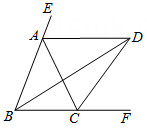
三、解答题

17. 如图，已知D为△ABC边BC延长线上一点，DF⊥AB于F交AC于E，∠A＝35°，∠D＝42°，求∠ACD的度数．

查看试题解析
18. 如图，已知AB=AD，AC=AE，∠BAE=∠DAC．求证：∠B=∠D．

查看试题解析
19. 已知△ABN和△ACM的位置如图所示，AB=AC，AD=AE，BD=CE．

(1)、求证：∠1=∠2；

(2)、求证：∠AME=∠AND．

查看试题解析
20. 如图，四边形ABCD中，BA丄DA，CD丄BC，BE、DF分别是∠ABC、∠ADC的平分线．

(1)、∠1与∠2有什么数量关系，为什么？

(2)、BE与DF有什么位置关系？请说明理由．

查看试题解析
21. 如图，AB=AC，直线 $l$ 经过点A，BM⊥ $l$ ， CN⊥ $l$ ，垂足分别为M、N，BM=AN．

(1)、求证：MN=BM＋CN；

(2)、求证：∠BAC=90°．

查看试题解析
22. 已知点M（ $m - 5$ ， $1 - 2 m$ ），解答下列问题：

(1)、若点M到x轴和y轴的距离相等，求点M的坐标；

(2)、若点M向右平移若干个单位后，与点N（-2，-3）关于y轴对称，求点M的坐标．

查看试题解析
23. 如图，在四边形ABCD中，∠B=120°，∠B与∠ADC互为补角，点E在BC上，将△DCE沿DE翻折，得到△DC'E，若AB∥C'E，DC'平分∠ADE，求∠A的度数．

查看试题解析
24. 如图，在△ABC中， $∠ C = 45 °$ ，点M、N分别在AB、AC上，D在BC上，且DM丄DN．

(1)、若DM丄AB，DN丄AC，D为BC的中点，求证：AD平分∠BAC．

(2)、若BD=CD，求证：MN＜BM＋CN．

查看试题解析
25. 如图，已知点B（-2，0），C（2，0），A为y轴正半轴上一点，点D为第二象限内的一个动点，M在BD的延长线上，CD交AB于点F，且∠ABD=∠ACD．

(1)、求证：∠BDC=∠BAC；

(2)、求证：DA平分∠CDM；

(3)、若在D点运动的过程中，始终有DC=DA+DB，在此过程中，∠BAC的度数是否变化？如果变化，请说明理由；如果不变，请求出∠BAC的度数？

查看试题解析