人教版九年级上对接中考知识点复习专项计划——正多边形和圆
试卷更新日期：2022-09-27 类型：复习试卷
一、单选题
-
1. 如图，正五边形ABCDE内接于⊙O，连接AC，则∠ACD的度数是 （ ）
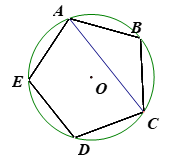A、72° B、70° C、60° D、45°2. ⊙O半径为4，以⊙O的内接正三角形、正方形、正六边形的边心距为边作一个三角形，则所得三角形的面积是（ ）A、2 B、 C、2 D、23. 如图，AE是四边形ABCD外接圆的直径， ， ， 则的度数为（ ）
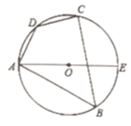A、50° B、55° C、60° D、65°4. 如图，在圆内接五边形中， ， 则的度数为（ ）
A、 B、 C、 D、5. 一个适当大的正六边形，它的一个顶点与一个边长为定值的小正六边形ABCDEF的中心O重合，且与边AB、CD相交于G、H（如图）.图中阴影部分的面积记为S，三条线段GB、BC、CH的长度之和记为l，大正六边形在绕点O旋转过程中，下列说法正确的是（ ）
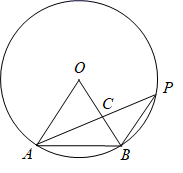
A、S变化，l不变 B、S不变，l变化 C、S变化，l变化 D、S与l均不变6. 如图，四边形 内接于圆 ，过 点作 于点 ，若 ， ，则 的长度为（ ）
A、 B、 C、 D、不能确定7. 如图，四边形 内接于 ，点 为边 上任意一点（点 不与点 ， 重合）连接 ．若 ，则 的度数可能为（ ）
A、 B、 C、 D、二、填空题
-
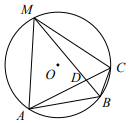
8. 是的内接正六边形一边，点P是优弧上的一点（点P不与点A，B重合）且 ， 与交于点C，则的度数为 ．
9. 如图，在⊙O中，AB是⊙O的内接正六边形的一边，BC是⊙O的内接正十边形的一边，则∠ABC＝°.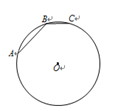
10. 如图，四边形ABCD是半圆O的内接四边形，其中AB是直径，点C是弧DB的中点，若∠C＝110°，则∠ABC的度数= ．
11. 如图，把分成相等的六段弧，依次连接各分点得到正六边形ABCDEF，如果的周长为 ， 那么该正六边形的边长是 ．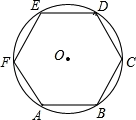
12. 如图，圆内接四边形ABCD，两组对边的延长线分别相交于点E、F，且∠E=40°，∠F=60°，则∠A= °
13. 如图，四边形ABCD内接于⊙O，AD∥BC，BD平分∠ABC，∠A＝126°，则∠BDC的度数为 ．
14. 如图，在⊙O的内接四边形ABCD中，∠BCD=130°，则∠BOD的度数是度．
15. 如图，A、B、C、D为一个正多边形的顶点，O为正多边形的中心，若∠ADB＝15°，则这个正多边形的边数为 ．
16. 如图，四边形ABCD内接于⊙O，点M在AD的延长线上，∠AOC＝142°，则∠CDM＝.
17. 如图，已知正方形ABCD和正△EGF都内接于⊙O，当EF∥BC时，的度数为 .
18. 如图，与正五边形ABCDE的边AB、DE分别相切于点B、D，则劣弧所对的圆心角的大小为度．
19. 如图，四边形ABCD是菱形，⊙O经过点A，C．D．与BC相交于点E，连接AC，AE．若∠ADC＝80°，则∠EAC的度数是 ．
三、解答题
-
20. 如图，四边形ABCD是平行四边形，∠DAC=45°，以线段AC为直径的圆与AB和AD的延长线分别交于点E和F，过点B作AC的垂线，垂足为H.求证：E，H，F三点共线.
21. 如图所示，⊙O的弦BD，CE所在直线相交于点A，若AB＝AC，求证：BD＝CE．
四、综合题
-
22. 如图，已知是等腰△ABC的外接圆，且AB＝AC，点D是上一点，连结BD并延长至点E，连结AD，CD.
(1)、求证：DA平分∠EDC.(2)、若∠EDA＝72°，求的度数.23. 如图，以四边形的对角线为直径作圆，圆心为O，点A、C在上，过点A作的延长线于点E，已知平分 ．
(1)、求证：是切线；(2)、若 ， ， 求的半径和的长．24. 如图，已知四边形ABCD内接于圆O，连接BD， ， ．
(1)、求证： ；(2)、若圆O的半径为3，求BC的长．25. 如图，△ABC与⊙O交于D，E两点，AB是直径且长为12，OD∥BC.
(1)、若∠B=40°，求∠A的度数；(2)、证明：CD=DE；(3)、若AD=4，求CE的长度.26. 如图，四边形 内接于 ， ， 平分 交 于点 ，连接 ， ， ， ．
(1)、求证：四边形 是菱形；(2)、若 ， ，求弦 的长．
