人教版九年级上对接中考知识点复习专项计划——图形的旋转
试卷更新日期:2022-09-27 类型:复习试卷
一、单选题
-
1. 如图,正方形网格中的每个小正方形的边长为1,将△ABC绕旋转中心旋转某个角度后得到△A'B'C'其中点A,B,C的对应点是点A',B',C',那么旋转中心是( )
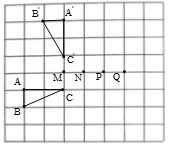 A、点Q B、点P C、点N D、点M2. 如图, 在 中, , 在同一平面内, 将 绕点 旋转到 的位置, 使得 , 则 是( )
A、点Q B、点P C、点N D、点M2. 如图, 在 中, , 在同一平面内, 将 绕点 旋转到 的位置, 使得 , 则 是( ) A、 B、 C、 D、3. △ABC在平面直角坐标系中的位置如图所示,将其绕点P顺时针旋转得到△A'B'C′,则点P的坐标是( )
A、 B、 C、 D、3. △ABC在平面直角坐标系中的位置如图所示,将其绕点P顺时针旋转得到△A'B'C′,则点P的坐标是( )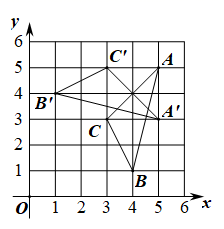 A、(4,5) B、(4,4) C、(3,5) D、(3,4)4. 如图,在正三角形网格中,以某点为中心,将 旋转,得到 ,则旋转中心是( )
A、(4,5) B、(4,4) C、(3,5) D、(3,4)4. 如图,在正三角形网格中,以某点为中心,将 旋转,得到 ,则旋转中心是( )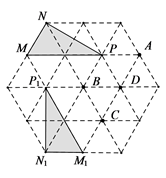 A、点A B、点B C、点C D、点D
A、点A B、点B C、点C D、点D二、填空题
-
5. 如图所示,绕点P顺时针旋转得到 , 则旋转的角度是 .
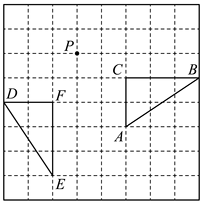 6. 如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为 .
6. 如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为 .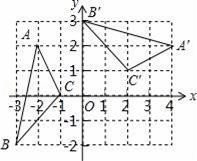 7. 如图,正方形 的对角线相交于点 ,点 是正方形 的一个顶点,如果两个正方形的边长相等,正方形 绕点 自由转动,设两个正方形重叠部分(阴影)的面积为 ,正方形 的面积为 .则 与 的关系是 .
7. 如图,正方形 的对角线相交于点 ,点 是正方形 的一个顶点,如果两个正方形的边长相等,正方形 绕点 自由转动,设两个正方形重叠部分(阴影)的面积为 ,正方形 的面积为 .则 与 的关系是 .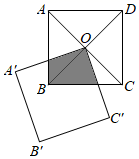 8. 如图,在正方形ABCD中,AB=8,点M在CD边上,且DM=2,△AEM与△ADM关于AM所在直线对称,将△ADM按顺时针方向绕点A旋转90°得到△ABF,连接EF,则线段EF的长为 .
8. 如图,在正方形ABCD中,AB=8,点M在CD边上,且DM=2,△AEM与△ADM关于AM所在直线对称,将△ADM按顺时针方向绕点A旋转90°得到△ABF,连接EF,则线段EF的长为 .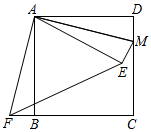 9. 在如图所示的正方形网格中, 绕某点旋转一定的角度,得到 ,则旋转中心可能是A,B,C,D中的点 .
9. 在如图所示的正方形网格中, 绕某点旋转一定的角度,得到 ,则旋转中心可能是A,B,C,D中的点 .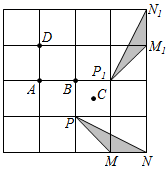
三、作图题
-
10. 如图,在平面直角坐标系中△ABC的三个顶点的坐标分别为A(5,4),B(0,3),C(2,1).
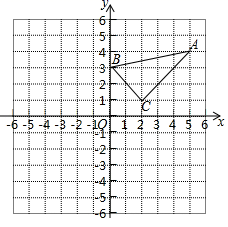
⑴画出△ABC关于原点成中心对称的△A1B1C1 , 并写出点C1的坐标;
⑵画出将△A1B1C1绕点C1按顺时针方向旋转90°所得的△A2B2C1 , 并写出点A2坐标.
11. 如图,在平面直角坐标系中,已知的三个顶点的坐标分别为 , 请按下列要求画图: (1)、将先向右平移4个单位长度、再向下平移1个单位长度,得到 , 画出;(2)、与关于原点O成中心对称,画出 .
(1)、将先向右平移4个单位长度、再向下平移1个单位长度,得到 , 画出;(2)、与关于原点O成中心对称,画出 .四、综合题
-
12. 在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点B逆时针旋转一个角度α后得到△DBE,点A,C的对应点分别为点D,E.
 (1)、如图1,若点D恰好落在边BC的延长线上,连接CE,求∠DEC的度数.(2)、如图2,若α=60°,F为BD的中点,连接CD,CF,EF,请判断四边形CDEF是什么特殊的四边形,并说明理由.13. 如图
(1)、如图1,若点D恰好落在边BC的延长线上,连接CE,求∠DEC的度数.(2)、如图2,若α=60°,F为BD的中点,连接CD,CF,EF,请判断四边形CDEF是什么特殊的四边形,并说明理由.13. 如图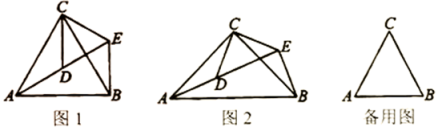 (1)、问题发现:如图1,和均为等边三角形,当旋转至点A,D,E在同一直线上,连接BE.则:
(1)、问题发现:如图1,和均为等边三角形,当旋转至点A,D,E在同一直线上,连接BE.则:①的度数为;
②线段BE,CE与AE之间的数量关系是 .
(2)、拓展研究:如图2,和均为等腰直角三角形, , 点A,D,E在同一直线上.若 , , 求AB的长度.(3)、探究发现:图1中的和 , 在旋转过程中,当点A,D,E不在同一直线上时,设直线AD与BE相交于点O,试在备用图中探索的度数,直接写出结果,不必说明理由.14. 如图①,在中, , , 点D,E分别在边 , 上,且 , 此时 , 成立.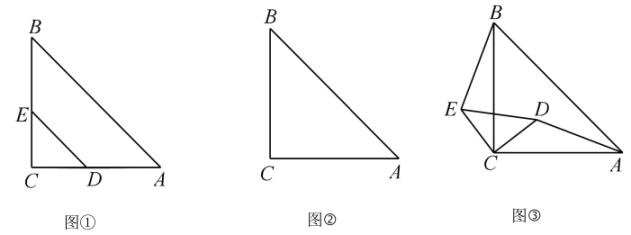 (1)、将绕点C逆时针旋转时,在图②中补充图形,并直接写出的长度;(2)、当绕点C逆时针旋转一周的过程中,与的数量关系和位置关系是否仍然成立?若成立,请你利用图③证明,若不成立请说明理由;(3)、将绕点C逆时针旋转一周的过程中,当A,D,E三点在同一条直线上时,请直接写出的长度.15. 综合与实践
(1)、将绕点C逆时针旋转时,在图②中补充图形,并直接写出的长度;(2)、当绕点C逆时针旋转一周的过程中,与的数量关系和位置关系是否仍然成立?若成立,请你利用图③证明,若不成立请说明理由;(3)、将绕点C逆时针旋转一周的过程中,当A,D,E三点在同一条直线上时,请直接写出的长度.15. 综合与实践问题情境:
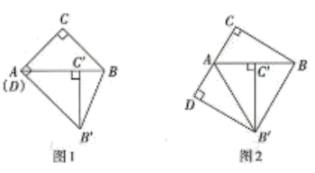
数学活动课上,同学们将绕点A顺时针旋转得到 , 点落在边AB上,连接 , 过点作于点D.
特例分析:
(1)、如图1,若点D与点A重合,请判断线段AC与BC之间的数量关系,并说明理由;探索发现:
(2)、如图2,若点D在线段CA的延长线上.且 , 请判断线段AD与之间的数最关系,并说明理由.16. 如图,已知,在中, , . 将绕点A逆时针旋转一个角至位置,连接BD,CE交于点F.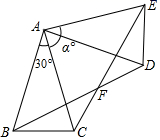 (1)、求证:(2)、若四边形ABFE为菱形,求的值;(3)、在(2)的条件下,若 , 直接写出CF的值.17. 与 都是等边三角形,连接AD、BE.
(1)、求证:(2)、若四边形ABFE为菱形,求的值;(3)、在(2)的条件下,若 , 直接写出CF的值.17. 与 都是等边三角形,连接AD、BE.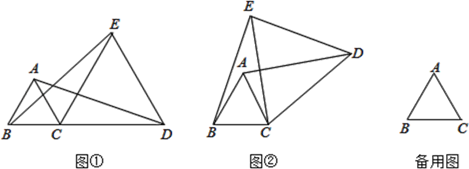 (1)、如图①,当点B、C、D在同一条直线上时,则 度;(2)、将图①中的 绕着点C逆时针旋转到如图②的位置,求证: .18.
(1)、如图①,当点B、C、D在同一条直线上时,则 度;(2)、将图①中的 绕着点C逆时针旋转到如图②的位置,求证: .18.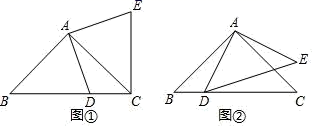 (1)、如图①,在 中, , 为 边上一点(不与点 , 重合),将线段 绕点 逆时针旋转90°得到 ,连接 ,试探索线段 , , 之间满足的等量关系,并证明你的结论.(2)、如图②,在 与 中, , ,将 绕点 旋转,使点 落在 边上,试探索线段 , , 之间满足的等量关系,并证明你的结论.19. 四边形ABCD是菱形,∠ABC=60°,E是对角线BD上的一个动点,连接AE,将线段AE绕点A逆时针旋转120°得到线段AF,连接EF,DF.
(1)、如图①,在 中, , 为 边上一点(不与点 , 重合),将线段 绕点 逆时针旋转90°得到 ,连接 ,试探索线段 , , 之间满足的等量关系,并证明你的结论.(2)、如图②,在 与 中, , ,将 绕点 旋转,使点 落在 边上,试探索线段 , , 之间满足的等量关系,并证明你的结论.19. 四边形ABCD是菱形,∠ABC=60°,E是对角线BD上的一个动点,连接AE,将线段AE绕点A逆时针旋转120°得到线段AF,连接EF,DF.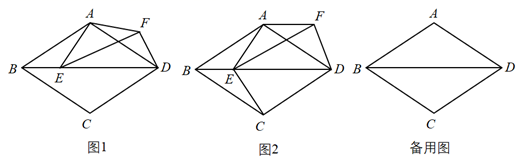 (1)、如图1,求∠BDF的度数;(2)、如图2,当DB=3DF时,连接EC,求证:四边形FECD是矩形;(3)、若G为DF中点,连接EG,当线段BD与DF满足怎样的数量关系时,四边形AEGF是菱形,并说明理由.20. 如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.易证:CE=CF.
(1)、如图1,求∠BDF的度数;(2)、如图2,当DB=3DF时,连接EC,求证:四边形FECD是矩形;(3)、若G为DF中点,连接EG,当线段BD与DF满足怎样的数量关系时,四边形AEGF是菱形,并说明理由.20. 如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.易证:CE=CF.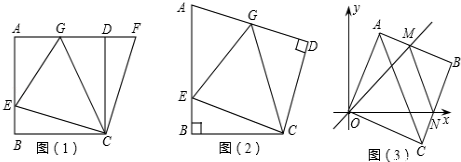 (1)、在图1中,若G在AD上,且∠GCE=45°.试猜想GE,BE,GD三线段之间的数量关系,并证明你的结论.(2)、运用(1)中解答所积累的经验和知识,完成下面两题:
(1)、在图1中,若G在AD上,且∠GCE=45°.试猜想GE,BE,GD三线段之间的数量关系,并证明你的结论.(2)、运用(1)中解答所积累的经验和知识,完成下面两题:①如图2,在四边形ABCD中∠B=∠D=90°,BC=CD,点E,点G分别是AB边,AD边上的动点.若∠BCD=α,∠ECG=β,试探索当α和β满足什么关系时,图1中GE,BE,GD三线段之间的关系仍然成立,并说明理由.
②在平面直角坐标中,边长为1的正方形OABC的两顶点A,C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图3).设△MBN的周长为p,在旋转正方形OABC的过程中,p值是否有变化?若不变,请直接写出结论.
21. 将矩形ABCD绕着点C按顺时针方向旋转得到矩形FECG,其中点E与点B,点G与点D分别是对应点,连接BG.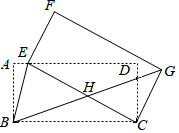 (1)、如图,若点A,E,D第一次在同一直线上,BG与CE交于点H,连接BE.
(1)、如图,若点A,E,D第一次在同一直线上,BG与CE交于点H,连接BE.①求证:BE平分∠AEC.
②取BC的中点P,连接PH,求证:PHCG.
③若BC=2AB=2,求BG的长.
(2)、若点A,E,D第二次在同一直线上,BC=2AB=4,直接写出点D到BG的距离.22. 已知△ABC和△ADE都是等腰三角形,AB=AC,AD=AE,∠DAE=∠BAC.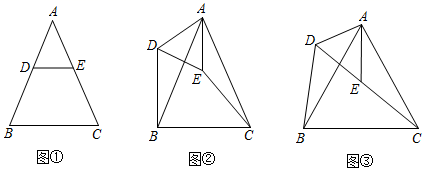
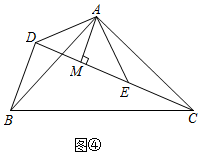 (1)、(初步感知)特殊情形:如图①,若点D,E分别在边AB,AC上,则DBEC.(填>、<或=)(2)、发现证明:如图②,将图①中△ADE的绕点A旋转,当点D在△ABC外部,点E在△ABC内部时,求证:DB=EC.(3)、条直线上,则∠CDB的度数为 ;线段CE,BD之间的数量关系为 .(4)、如图④,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,点C、D、E在同一直线上,AM为△ADE中DE边上的高,则∠CDB的度数为 ;线段AM,BD,CD之间的数量关系为 .23. (探索发现)如图①,四边形ABCD是正方形,M,N分别在边CD、BC上,且 , 我们把这种模型称为“半角模型”,在解决“半角模型”问题时,旋转是一种常用的方法.如图①,将绕点A顺时针旋转 , 点D与点B重合,得到 , 连接AM、AN、MN.
(1)、(初步感知)特殊情形:如图①,若点D,E分别在边AB,AC上,则DBEC.(填>、<或=)(2)、发现证明:如图②,将图①中△ADE的绕点A旋转,当点D在△ABC外部,点E在△ABC内部时,求证:DB=EC.(3)、条直线上,则∠CDB的度数为 ;线段CE,BD之间的数量关系为 .(4)、如图④,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,点C、D、E在同一直线上,AM为△ADE中DE边上的高,则∠CDB的度数为 ;线段AM,BD,CD之间的数量关系为 .23. (探索发现)如图①,四边形ABCD是正方形,M,N分别在边CD、BC上,且 , 我们把这种模型称为“半角模型”,在解决“半角模型”问题时,旋转是一种常用的方法.如图①,将绕点A顺时针旋转 , 点D与点B重合,得到 , 连接AM、AN、MN.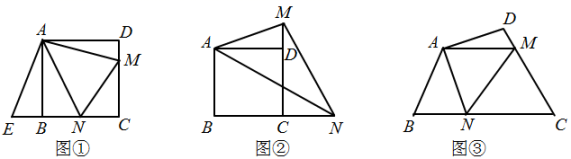 (1)、试判断DM,BN,MN之间的数量关系,并写出证明过程.(2)、如图②,点M、N分别在正方形ABCD的边BC、CD的延长线上, , 连接MN,请写出MN、DM、BN之间的数量关系,并写出证明过程.(3)、如图③,在四边形ABCD中,AB=AD, , , 点N,M分别在边BC,CD上, , 请直接写出线段BN,DM,MN之间的数量关系.24. 如图,把长方形ABCD绕点A按逆时针方向旋转得到长方形AEFG,使点E落在对角线BD上,连接DG,DF.
(1)、试判断DM,BN,MN之间的数量关系,并写出证明过程.(2)、如图②,点M、N分别在正方形ABCD的边BC、CD的延长线上, , 连接MN,请写出MN、DM、BN之间的数量关系,并写出证明过程.(3)、如图③,在四边形ABCD中,AB=AD, , , 点N,M分别在边BC,CD上, , 请直接写出线段BN,DM,MN之间的数量关系.24. 如图,把长方形ABCD绕点A按逆时针方向旋转得到长方形AEFG,使点E落在对角线BD上,连接DG,DF. (1)、若∠BAE=50°,求∠DGF的度数;(2)、求证:DF = DC;(3)、若S△ABE+S△DFG = S△ADG , 直接写出 的值.
(1)、若∠BAE=50°,求∠DGF的度数;(2)、求证:DF = DC;(3)、若S△ABE+S△DFG = S△ADG , 直接写出 的值.