人教版九年级上对接中考知识点复习专项计划——二次函数的应用之动态几何问题(不含相似及三角函数九上适用)
试卷更新日期:2022-09-27 类型:复习试卷
一、综合题
-
1. 如图1,抛物线与x轴交于 , 两点,与y轴交于点C.
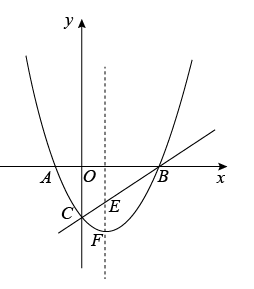
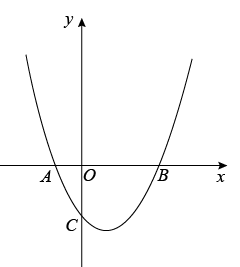
图1 图2
(1)、求该抛物线的解析式;(2)、若点E是抛物线的对称轴与直线BC的交点,点F是抛物线的顶点,求EF的长;(3)、设点P是(1)中抛物线上的一个动点,是否存在满足的点P?如果存在,请求出点P的坐标;若不存在,请说明理由.(请在图2中探讨)2. 如图,抛物线与轴交于 , 两点,与轴交于点,直线方程为 .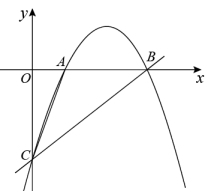 (1)、求抛物线的解析式;(2)、点为抛物线上一点,若 , 请直接写出点的坐标;(3)、点是抛物线上一点,若 , 求点的坐标.3. 如图,抛物线 (b,c是常数)的顶点为C,与x轴交于A,B两点, , ,点P为线段 上的动点,过P作 交 于点Q.
(1)、求抛物线的解析式;(2)、点为抛物线上一点,若 , 请直接写出点的坐标;(3)、点是抛物线上一点,若 , 求点的坐标.3. 如图,抛物线 (b,c是常数)的顶点为C,与x轴交于A,B两点, , ,点P为线段 上的动点,过P作 交 于点Q. (1)、求该抛物线的解析式;(2)、求 面积的最大值,并求此时P点坐标.4. 如图,抛物线与x轴交于点A,B,与y轴交于点C,一次函数y=-x+3的图象经过点B,C,与抛物线对称轴交于点D,且 , 点P是抛物线上的动点.
(1)、求该抛物线的解析式;(2)、求 面积的最大值,并求此时P点坐标.4. 如图,抛物线与x轴交于点A,B,与y轴交于点C,一次函数y=-x+3的图象经过点B,C,与抛物线对称轴交于点D,且 , 点P是抛物线上的动点.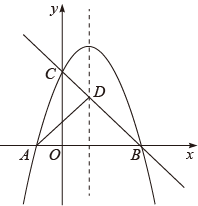 (1)、求抛物线的函数解析式.(2)、当点P在直线BC上方时,求点P到直线BC的距离的最大值.5. 如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点B,抛物线经过A、B两点,且与x轴的负半轴交于点C.
(1)、求抛物线的函数解析式.(2)、当点P在直线BC上方时,求点P到直线BC的距离的最大值.5. 如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点B,抛物线经过A、B两点,且与x轴的负半轴交于点C.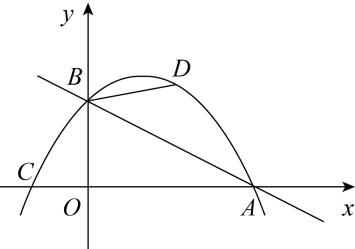 (1)、求该抛物线的解析式;(2)、若点D为直线上方抛物线上的一点, , 直接写出点D的坐标.6. 如图,抛物线经过、两点,与轴交于点 , 点是抛物线上一动点,设点的横坐标为 , 连结、、、 .
(1)、求该抛物线的解析式;(2)、若点D为直线上方抛物线上的一点, , 直接写出点D的坐标.6. 如图,抛物线经过、两点,与轴交于点 , 点是抛物线上一动点,设点的横坐标为 , 连结、、、 .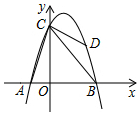 (1)、求抛物线的函数表达式.(2)、当的面积等于的面积的时,求的值.(3)、当时,若点是轴上一动点,点是抛物线上一动点,试判断是否存在这样的点 , 使得以点、、、为顶点的四边形是平行四边形?若存在,请直接写出点的的坐标;若不存在,请说明理由.7. 已知抛物线与x轴有公共点.
(1)、求抛物线的函数表达式.(2)、当的面积等于的面积的时,求的值.(3)、当时,若点是轴上一动点,点是抛物线上一动点,试判断是否存在这样的点 , 使得以点、、、为顶点的四边形是平行四边形?若存在,请直接写出点的的坐标;若不存在,请说明理由.7. 已知抛物线与x轴有公共点.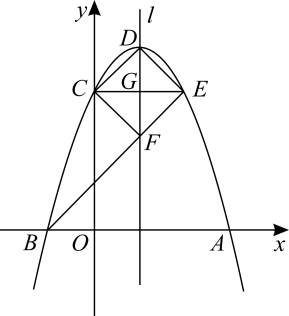 (1)、当y随x的增大而增大时,求自变量x的取值范围;(2)、将抛物线先向上平移4个单位长度,再向右平移n个单位长度得到抛物线(如图所示),抛物线与x轴交于点A,B(点A在点B的右侧),与y轴交于点C.当OC=OA时,求n的值;(3)、D为抛物线的顶点,过点C作抛物线的对称轴l的垂线,垂足为G,交抛物线于点E,连接BE交l于点F.求证:四边形CDEF是正方形.8. 在平面直角坐标系xOy中,已知抛物线y=-x2+2mx+3m,点A(3,0).
(1)、当y随x的增大而增大时,求自变量x的取值范围;(2)、将抛物线先向上平移4个单位长度,再向右平移n个单位长度得到抛物线(如图所示),抛物线与x轴交于点A,B(点A在点B的右侧),与y轴交于点C.当OC=OA时,求n的值;(3)、D为抛物线的顶点,过点C作抛物线的对称轴l的垂线,垂足为G,交抛物线于点E,连接BE交l于点F.求证:四边形CDEF是正方形.8. 在平面直角坐标系xOy中,已知抛物线y=-x2+2mx+3m,点A(3,0).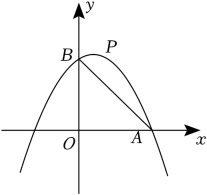 (1)、当抛物线过点A时,求抛物线的解析式;(2)、证明:无论m为何值,抛物线必过定点D,并求出点D的坐标;(3)、在(1)的条件下,抛物线与y轴交于点B,点P是抛物线上位于第一象限的点,连接AB,PD交于点M,PD与y轴交于点N.设S=S△PAM-S△BMN,问是否存在这样的点P,使得S有最大值?若存在,请求出点P的坐标,并求出S的最大值;若不存在,请说明理由.9. 如图①,已知抛物线L:y=x2+bx+c的图象经过点A(0,3),B(1,0),过点A作ACx轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点.
(1)、当抛物线过点A时,求抛物线的解析式;(2)、证明:无论m为何值,抛物线必过定点D,并求出点D的坐标;(3)、在(1)的条件下,抛物线与y轴交于点B,点P是抛物线上位于第一象限的点,连接AB,PD交于点M,PD与y轴交于点N.设S=S△PAM-S△BMN,问是否存在这样的点P,使得S有最大值?若存在,请求出点P的坐标,并求出S的最大值;若不存在,请说明理由.9. 如图①,已知抛物线L:y=x2+bx+c的图象经过点A(0,3),B(1,0),过点A作ACx轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点.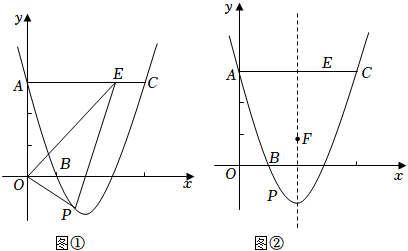 (1)、求抛物线的关系式;(2)、若动点P在直线OE下方的抛物线上,连结PE、PO,当△OPE面积最大时,求出P点坐标;(3)、将抛物线L向上平移h个单位长度,使平移后所得抛物线的顶点落在△OAE内(包括△OAE的边界),求h的取值范围;(4)、如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P,使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.10. 如图,在平面直角坐标系中,抛物线y=ax2+bx+2经过A( , 0),B(3,)两点,与y轴交于点C.
(1)、求抛物线的关系式;(2)、若动点P在直线OE下方的抛物线上,连结PE、PO,当△OPE面积最大时,求出P点坐标;(3)、将抛物线L向上平移h个单位长度,使平移后所得抛物线的顶点落在△OAE内(包括△OAE的边界),求h的取值范围;(4)、如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P,使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.10. 如图,在平面直角坐标系中,抛物线y=ax2+bx+2经过A( , 0),B(3,)两点,与y轴交于点C.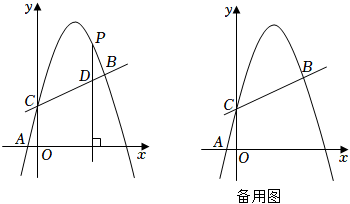 (1)、求抛物线的解析式;(2)、点P在抛物线上,过P作PD⊥x轴,交直线BC于点D,若以P、D、O、C为顶点的四边形是平行四边形,求点P的横坐标;(3)、抛物线上是否存在点Q,使∠QCB=45°?若存在,请直接写出点Q的坐标;若不存在,请说明理由.11. 如图,已知直线y=x+4与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c经过A,C两点,且与x轴的另一个交点为B,对称轴为直线x=﹣1.
(1)、求抛物线的解析式;(2)、点P在抛物线上,过P作PD⊥x轴,交直线BC于点D,若以P、D、O、C为顶点的四边形是平行四边形,求点P的横坐标;(3)、抛物线上是否存在点Q,使∠QCB=45°?若存在,请直接写出点Q的坐标;若不存在,请说明理由.11. 如图,已知直线y=x+4与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c经过A,C两点,且与x轴的另一个交点为B,对称轴为直线x=﹣1.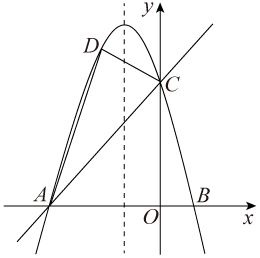 (1)、求抛物线的表达式;(2)、D是第二象限内抛物线上的动点,设点D的横坐标为m,求四边形ABCD面积S的最大值及此时D点的坐标;(3)、若点P在抛物线对称轴上,是否存在点P,Q,使以点A,C,P,Q为顶点的四边形是以AC为对角线的菱形?若存在,请求出P,Q两点的坐标;若不存在,请说明理由.12. 如图,抛物线与x轴交于点 , 点 , 与y轴交于点C.
(1)、求抛物线的表达式;(2)、D是第二象限内抛物线上的动点,设点D的横坐标为m,求四边形ABCD面积S的最大值及此时D点的坐标;(3)、若点P在抛物线对称轴上,是否存在点P,Q,使以点A,C,P,Q为顶点的四边形是以AC为对角线的菱形?若存在,请求出P,Q两点的坐标;若不存在,请说明理由.12. 如图,抛物线与x轴交于点 , 点 , 与y轴交于点C.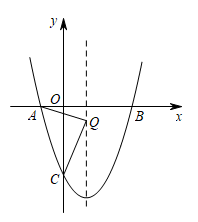 (1)、求抛物线的表达式;(2)、在对称轴上找一点Q,使的周长最小,求点Q的坐标;(3)、点P是抛物线对称轴上的一点,点M是对称轴左侧抛物线上的一点,当是以为腰的等腰直角三角形时,请直接写出所有点M的坐标.13. 如图,抛物线与轴交于 , 两点,与轴交于点 , 连接 .
(1)、求抛物线的表达式;(2)、在对称轴上找一点Q,使的周长最小,求点Q的坐标;(3)、点P是抛物线对称轴上的一点,点M是对称轴左侧抛物线上的一点,当是以为腰的等腰直角三角形时,请直接写出所有点M的坐标.13. 如图,抛物线与轴交于 , 两点,与轴交于点 , 连接 .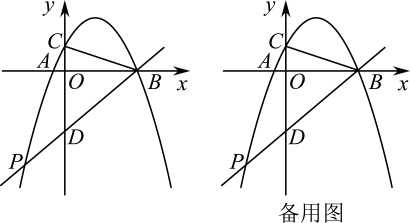 (1)、求抛物线的解析式.(2)、点是第三象限抛物线上一点,直线与轴交于点 , 的面积为12,求点的坐标.(3)、在(2)的条件下,若点是线段上点,连接 , 将沿直线翻折得到 , 当直线与直线相交所成锐角为时,求点的坐标.14. 如图,抛物线的对称轴是直线 , 与轴交于点 , , 与轴交于点 , 连接.
(1)、求抛物线的解析式.(2)、点是第三象限抛物线上一点,直线与轴交于点 , 的面积为12,求点的坐标.(3)、在(2)的条件下,若点是线段上点,连接 , 将沿直线翻折得到 , 当直线与直线相交所成锐角为时,求点的坐标.14. 如图,抛物线的对称轴是直线 , 与轴交于点 , , 与轴交于点 , 连接. (1)、求此抛物线的解析式;(2)、已知点是第一象限内抛物线上的一个动点,过点作轴,垂足为点 , 交直线于点 , 是否存在这样的点 , 使得以 , , 为顶点的三角形是等腰三角形.若存在,请求出点的坐标,若不存在,请说明理由;(3)、已知点是抛物线对称轴上的点,在坐标平面内是否存在点 , 使以点、、、为顶点的四边形为矩形,若存在,请直接写出点的坐标;若不存在,请说明理由.15. 探索发现
(1)、求此抛物线的解析式;(2)、已知点是第一象限内抛物线上的一个动点,过点作轴,垂足为点 , 交直线于点 , 是否存在这样的点 , 使得以 , , 为顶点的三角形是等腰三角形.若存在,请求出点的坐标,若不存在,请说明理由;(3)、已知点是抛物线对称轴上的点,在坐标平面内是否存在点 , 使以点、、、为顶点的四边形为矩形,若存在,请直接写出点的坐标;若不存在,请说明理由.15. 探索发现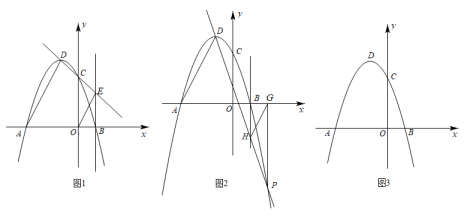 (1)、在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)与x轴交于点A(﹣3,0),B(1,0),与y轴交于点C,顶点为点D,连接AD.
(1)、在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)与x轴交于点A(﹣3,0),B(1,0),与y轴交于点C,顶点为点D,连接AD.①如图1,直线DC交直线x=1于点E,连接OE.求证:AD∥OE;
②如图2,点P(2,﹣5)为抛物线y=ax2+bx+3(a≠0)上一点,过点P作PG⊥x轴,垂足为点G.直线DP交直线x=1于点H,连接HG.求证:AD∥HG;
(2)、通过上述两种特殊情况的证明,你是否有所发现?请仿照(1)写出你的猜想,并在图3上画出草图.在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)与x轴交于点A(﹣3,0),B(1,0),顶点为点D.点M为该抛物线上一动点(不与点A,B,D重合),猜想:作MN⊥x轴于N,直线DM交直线x=1于Q,则QN∥AD,证明见解析
16. 综合与探究如图,某一次函数与二次函数的图象交点为A(-1,0),B(4,5).
 (1)、求抛物线的解析式;(2)、点C为抛物线对称轴上一动点,当AC与BC的和最小时,点C的坐标为 ;(3)、点D为抛物线位于线段AB下方图象上一动点,过点D作DE⊥x轴,交线段AB于点E,求线段DE长度的最大值;(4)、在(2)条件下,点M为y轴上一点,点F为直线AB上一点,点N为平面直角坐标系内一点,若以点C,M,F,N为顶点的四边形是正方形,请直接写出点N的坐标.17. 如图,抛物线交y轴于点 , 并经过点 , 过点A作轴交抛物线于点B,抛物线的对称轴为直线 , D点的坐标为 , 连接 , , .点E从A点出发,以每秒个单位长度的速度沿着射线运动,设点E的运动时间为m秒,过点E作于F,以为对角线作正方形 .
(1)、求抛物线的解析式;(2)、点C为抛物线对称轴上一动点,当AC与BC的和最小时,点C的坐标为 ;(3)、点D为抛物线位于线段AB下方图象上一动点,过点D作DE⊥x轴,交线段AB于点E,求线段DE长度的最大值;(4)、在(2)条件下,点M为y轴上一点,点F为直线AB上一点,点N为平面直角坐标系内一点,若以点C,M,F,N为顶点的四边形是正方形,请直接写出点N的坐标.17. 如图,抛物线交y轴于点 , 并经过点 , 过点A作轴交抛物线于点B,抛物线的对称轴为直线 , D点的坐标为 , 连接 , , .点E从A点出发,以每秒个单位长度的速度沿着射线运动,设点E的运动时间为m秒,过点E作于F,以为对角线作正方形 .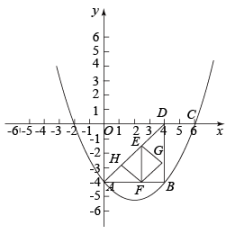
 (1)、求抛物线的解析式;(2)、当点G随着E点运动到达上时,求此时m的值和点G的坐标;(3)、在运动的过程中,是否存在以B,G,C和平面内的另一点为顶点的四边形是矩形,如果存在,直接写出点G的坐标,如果不存在,请说明理由.18. 已知抛物线(a,b,c是常数,)的顶点为P,与x轴相交于点和点B.(1)、若 ,
(1)、求抛物线的解析式;(2)、当点G随着E点运动到达上时,求此时m的值和点G的坐标;(3)、在运动的过程中,是否存在以B,G,C和平面内的另一点为顶点的四边形是矩形,如果存在,直接写出点G的坐标,如果不存在,请说明理由.18. 已知抛物线(a,b,c是常数,)的顶点为P,与x轴相交于点和点B.(1)、若 ,①求点P的坐标;
②直线(m是常数,)与抛物线相交于点M,与相交于点G,当取得最大值时,求点M,G的坐标;
(2)、若 , 直线与抛物线相交于点N,E是x轴的正半轴上的动点,F是y轴的负半轴上的动点,当的最小值为5时,求点E,F的坐标.19. 如图,在平面直角坐标系中,抛物线与x轴相交于点A、B(点A在点B的左侧),与y轴相交于点C,连接 .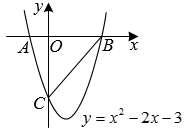 (1)、求线段AC的长;(2)、若点Р为该抛物线对称轴上的一个动点,当时,求点P的坐标;(3)、若点M为该抛物线上的一个动点,当为直角三角形时,求点M的坐标.20. 如图1,在平面直角坐标系中,已知二次函数 的图象经过点 , ,与y轴交于点C.
(1)、求线段AC的长;(2)、若点Р为该抛物线对称轴上的一个动点,当时,求点P的坐标;(3)、若点M为该抛物线上的一个动点,当为直角三角形时,求点M的坐标.20. 如图1,在平面直角坐标系中,已知二次函数 的图象经过点 , ,与y轴交于点C. (1)、求该二次函数的表达式;(2)、连接 ,在该二次函数图象上是否存在点P,使 ?若存在,请求出点P的坐标:若不存在,请说明理由;(3)、如图2,直线l为该二次函数图象的对称轴,交x轴于点E.若点Q为x轴上方二次函数图象上一动点,过点Q作直线 , 分别交直线l于点M,N,在点Q的运动过程中, 的值是否为定值?若是,请求出该定值;若不是,请说明理由.21. 如图,在平面直角坐标系中,抛物线 与直线AB交于点A(0,-4),B(4,0).
(1)、求该二次函数的表达式;(2)、连接 ,在该二次函数图象上是否存在点P,使 ?若存在,请求出点P的坐标:若不存在,请说明理由;(3)、如图2,直线l为该二次函数图象的对称轴,交x轴于点E.若点Q为x轴上方二次函数图象上一动点,过点Q作直线 , 分别交直线l于点M,N,在点Q的运动过程中, 的值是否为定值?若是,请求出该定值;若不是,请说明理由.21. 如图,在平面直角坐标系中,抛物线 与直线AB交于点A(0,-4),B(4,0).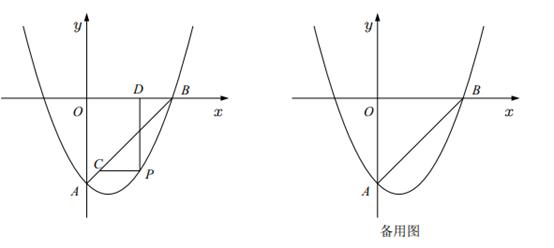 (1)、求该抛物线的函数表达式;(2)、点P是直线AB下方拋物线上的一动点,过点P作x轴的平行线交AB于点C,过点P作y轴的平行线交x轴于点D,求PC+PD的最大值及此时点P的坐标;(3)、在(2)中PC+PD取得最大值的条件下,将该抛物线沿水平方向向左平移5个单位,点E为点P的对应点,平移后的抛物线与y轴交于点F,M为平移后的抛物线的对称轴上一点.在平移后的抛物线上确定一点N,使得以点E,F,M,N为顶点的四边形是平行四边形,写出所有符合条件的点N的坐标,并写出求解点N的坐标的其中一种情况的过程.22. 如图,四边形的顶点坐标分别为 , , , , 抛物线经过 , , 三点.
(1)、求该抛物线的函数表达式;(2)、点P是直线AB下方拋物线上的一动点,过点P作x轴的平行线交AB于点C,过点P作y轴的平行线交x轴于点D,求PC+PD的最大值及此时点P的坐标;(3)、在(2)中PC+PD取得最大值的条件下,将该抛物线沿水平方向向左平移5个单位,点E为点P的对应点,平移后的抛物线与y轴交于点F,M为平移后的抛物线的对称轴上一点.在平移后的抛物线上确定一点N,使得以点E,F,M,N为顶点的四边形是平行四边形,写出所有符合条件的点N的坐标,并写出求解点N的坐标的其中一种情况的过程.22. 如图,四边形的顶点坐标分别为 , , , , 抛物线经过 , , 三点. (1)、求证:四边形是矩形;(2)、求抛物线的解析式;(3)、绕平面内一点顺时针旋转得到 , 即点 , , 的对应点分别为 , , , 若恰好两个顶点落在抛物线上,请直接写出的坐标.23. 如图,已知抛物线与x轴交于点 , 两点,与y轴交于点C,点P是直线BC下方抛物线上一动点,过点P作直线轴,交直线BC于点D,交x轴于点F,以PD为斜边,在PD的右侧作等腰直角 .
(1)、求证:四边形是矩形;(2)、求抛物线的解析式;(3)、绕平面内一点顺时针旋转得到 , 即点 , , 的对应点分别为 , , , 若恰好两个顶点落在抛物线上,请直接写出的坐标.23. 如图,已知抛物线与x轴交于点 , 两点,与y轴交于点C,点P是直线BC下方抛物线上一动点,过点P作直线轴,交直线BC于点D,交x轴于点F,以PD为斜边,在PD的右侧作等腰直角 .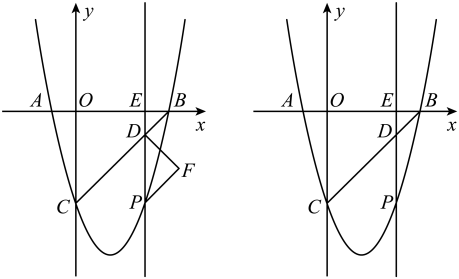 (1)、求抛物线的表达式,并直接写出直线BC的表达式;(2)、设点P的横坐标为m(),在点P运动的过程中,当等腰直角的面积为9时,请求出m的值;(3)、连接AC,该抛物线上是否存在一点M,使 , 若存在,请直接写出所有符合条件的点M的坐标,若不存在,请说明理由.24. 如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点B.抛物线经过点A、点B.
(1)、求抛物线的表达式,并直接写出直线BC的表达式;(2)、设点P的横坐标为m(),在点P运动的过程中,当等腰直角的面积为9时,请求出m的值;(3)、连接AC,该抛物线上是否存在一点M,使 , 若存在,请直接写出所有符合条件的点M的坐标,若不存在,请说明理由.24. 如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点B.抛物线经过点A、点B. (1)、求抛物线的函数表达式并直接写出顶点的坐标;(2)、若在第三象限的抛物线上有一动点M,当点M到直线AB的距离最大时,求点M的坐标;(3)、点C,D分别为线段AO,线段AB上的点,且 , 连接CD.将线段CD绕点D顺时针旋转90度,点C旋转后的对应点为点E,连接OE.当线段OE的长最小时,请直接写出直线DE的函数表达式 .25. 已知抛物线y=ax2+bx+3经过点A (1,0)和点B (-3,0),与y轴交于点C,点P为第二象限内抛物线上的动点.
(1)、求抛物线的函数表达式并直接写出顶点的坐标;(2)、若在第三象限的抛物线上有一动点M,当点M到直线AB的距离最大时,求点M的坐标;(3)、点C,D分别为线段AO,线段AB上的点,且 , 连接CD.将线段CD绕点D顺时针旋转90度,点C旋转后的对应点为点E,连接OE.当线段OE的长最小时,请直接写出直线DE的函数表达式 .25. 已知抛物线y=ax2+bx+3经过点A (1,0)和点B (-3,0),与y轴交于点C,点P为第二象限内抛物线上的动点.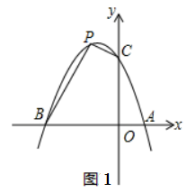

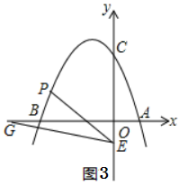 (1)、抛物线的解析式为 , 抛物线的顶点坐标为;(2)、如图1,是否存在点P,使四边形BOCP的面积为8?若存在,请求出点P的坐标;若不存在,请说明理由.(3)、如图2,连接OP交BC于点D,当S△CPD∶S△BPD=1∶2时,请求出点D的坐标;(4)、如图3,点E的坐标为(0,-1),点G为x轴负半轴上的一点,∠OGE=15°,连接PE,若∠PEG=2∠OGE,请求出点P的坐标.26. 综合与探究
(1)、抛物线的解析式为 , 抛物线的顶点坐标为;(2)、如图1,是否存在点P,使四边形BOCP的面积为8?若存在,请求出点P的坐标;若不存在,请说明理由.(3)、如图2,连接OP交BC于点D,当S△CPD∶S△BPD=1∶2时,请求出点D的坐标;(4)、如图3,点E的坐标为(0,-1),点G为x轴负半轴上的一点,∠OGE=15°,连接PE,若∠PEG=2∠OGE,请求出点P的坐标.26. 综合与探究如图,已知抛物线与x轴负半轴交于点 , 与y轴交于点 , 抛物线的顶点为D,直线y=x+b与抛物线交于A,F两点,过点D作DE∥y轴交直线AF于点E.
 (1)、求抛物线和直线AF的解析式;(2)、在直线AF上方的抛物线上有一点P,使 , 求点P的坐标;(3)、若点M为抛物线上一动点,试探究在直线AF上是否存在一点N,使得以D,E,M,N为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.27. 已知抛物线与x轴交于 , 两点,交y轴于点C,点P是抛物线上一个动点,且点P的横坐标为m.
(1)、求抛物线和直线AF的解析式;(2)、在直线AF上方的抛物线上有一点P,使 , 求点P的坐标;(3)、若点M为抛物线上一动点,试探究在直线AF上是否存在一点N,使得以D,E,M,N为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.27. 已知抛物线与x轴交于 , 两点,交y轴于点C,点P是抛物线上一个动点,且点P的横坐标为m.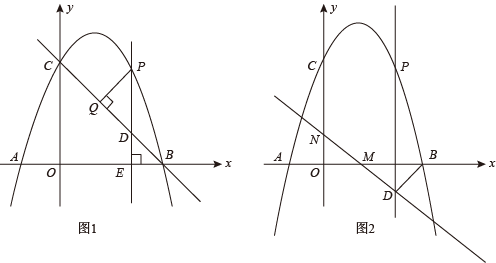 (1)、求抛物线的解析式;(2)、如图1,若点P在上方的抛物线上运动(不与B、C重合),过点P作x轴的垂线,垂足为E,交于点D,过点P作的垂线,垂足为Q,若 , 求m的值;(3)、如图2,将直线沿y轴向下平移5个单位,交x轴于点M,交y轴于点N.过点P作x轴的垂线,交直线于点D,是否存在一点P,使是等腰三角形?若存在,请直接写出符合条件的m的值;若不存在,请说明理由.28. 如图,抛物线与轴交于、两点,与轴交于点 , 抛物线的对称轴交轴于点 .
(1)、求抛物线的解析式;(2)、如图1,若点P在上方的抛物线上运动(不与B、C重合),过点P作x轴的垂线,垂足为E,交于点D,过点P作的垂线,垂足为Q,若 , 求m的值;(3)、如图2,将直线沿y轴向下平移5个单位,交x轴于点M,交y轴于点N.过点P作x轴的垂线,交直线于点D,是否存在一点P,使是等腰三角形?若存在,请直接写出符合条件的m的值;若不存在,请说明理由.28. 如图,抛物线与轴交于、两点,与轴交于点 , 抛物线的对称轴交轴于点 .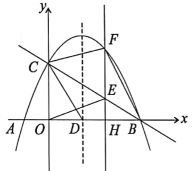 (1)、求的值;(2)、在抛物线对称轴上找点 , 使是以为腰的等腰三角形,请求出点的坐标;(提醒满足条件的点可能不只一个)(3)、点是线段上一个动点,过点作轴的垂线与抛物线相交于点 , 与轴相交于点 , 连接、、 , 当四边形的面积最大时,请你说明四边形的形状.
(1)、求的值;(2)、在抛物线对称轴上找点 , 使是以为腰的等腰三角形,请求出点的坐标;(提醒满足条件的点可能不只一个)(3)、点是线段上一个动点,过点作轴的垂线与抛物线相交于点 , 与轴相交于点 , 连接、、 , 当四边形的面积最大时,请你说明四边形的形状.