2022-2023学年苏科版数学七上尖子生考点培优专题训练3 定义新运算
试卷更新日期:2022-09-26 类型:复习试卷
一、单选题
-
1. 如果规定符号“*”的意义为:a*b , 则的值是( )A、6 B、-6 C、 D、-2. 现定义一种新运算“*”,规定 , 如 , 则等于( )A、11 B、-11 C、7 D、-73. 规定新运算“⊕”: 对于任意实数a、b都有 ,例如: , 则方 程 的解是( )A、 B、1 C、 D、4.
对于有理数 , ,定义 ,则 化简后得( )A、 B、 C、 D、5. 任意四个有理数a、b、c、d,定义了一种新运算: , 若 , 则x的值为( )A、2 B、3 C、6 D、6. 若“!”是一种数学运算符号,并且1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1,…,则 的值为( )A、2017 B、2016 C、2017! D、2016!7. 已知 = =3, = =10, = =15,……观察以上计算过程,寻找规律.计算 C85=( )A、72 B、56 C、42 D、408. 已知:[x]表示不大于x的最大整数.例:[3.6]=3,[﹣0.9]=﹣1,现定义:{x}=x﹣[x],例:{1.6}=1.6﹣[1.6]=0.6,计算{4.9}﹣{﹣1.8}的结果为( )A、6.7 B、3.1 C、1.1 D、0.79. 我们常用的十进制数,如2639=2×103+6×102+3×101+9,我国古代《易经》一书记载,远古时期,人们通过在绳子上打结来记录数量,如图,一位母亲在从右到左依次排列的绳子上打结,并采用七进制(如2513=2×73+5×72+1×71+3),用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是( ) A、1435天 B、565天 C、365天 D、13天10. 已知有理数 ,我们把 称为 的差倒数,如:2的差倒数是 ,-1的差倒数是 .如果 , 是 的差倒数, 是 的差倒数, 是 的差倒数…依此类推,那么 的值是( )A、-3 B、 C、 D、
A、1435天 B、565天 C、365天 D、13天10. 已知有理数 ,我们把 称为 的差倒数,如:2的差倒数是 ,-1的差倒数是 .如果 , 是 的差倒数, 是 的差倒数, 是 的差倒数…依此类推,那么 的值是( )A、-3 B、 C、 D、二、填空题
-
11. 规定一种新运算:a⊗b=a2﹣2b,若2⊗ [ 3 ⊗(﹣x)]=6,则x的值为12. 如果定义新运算: ,那么(1※2)※3的值为 .13. 定义一种新运算“※”:对于任意有理数x和y,x※y= (a为常数).例如:2※3=2×3+(2+3)a+1=5a+7.若2※(-1)的值为3,则a的值为.14. 定义新运算:对于任意实数a,b,都有a⊕b=a(a﹣b)+1,等式右边是通常的加法、减法及乘法运算,比如:2⊕5=2×(2﹣5)+1=2×(﹣3)+1=﹣6+1=﹣5.则(﹣2)⊕3= .15. 如图定义一种新运算“⊗”,如:2⊗1= =2;x⊗y= ,则(4⊗2)⊗(﹣1)= .16. 已知a,b均为有理数,现我们定义一种新的运算,规定:a#b=a2+ab﹣5,例如:1#2=12+1×2﹣5=﹣2,则(﹣3)#6的值是 .17. 已知a,b为有理数,如果规定一种新的运算“※”,规定:a※b=2b﹣3a,例如:1※2=2×2﹣3×1=4﹣3=1,计算:(3※2)※5= .18. 符号“ ”表示和,如 ,则 .19. 符号“”表示一种运算,它对一些数的运算结果如下:
① , , , , …;
② , , , , ….
利用以上规律计算:= .
20. 在计算的值时,可设 , ①则②.∴②-①,得 , 所以 , 试利用上述方法求的值: .三、解答题
-
21. 若“三角
 表示运算a﹣b+c,“方框”
表示运算a﹣b+c,“方框”  表示运算x﹣y+z+w.求:
表示运算x﹣y+z+w.求:  ×
×  表示的运算,并计算结果. 22. 已知x,y为有理数,现规定一种新运算“”,满足 .(1)、求的值;(2)、记 , , 请猜想P与Q的数量关系,并说明理由.23. 设为实数,则我们把形如的式子叫做二阶行列式,它的运算法则用公式表示为 , 请利用此法则解决以下问题:(1)、求的值;(2)、若 , 求的值.24. 用“☆”定义一种新运算:对于任意有理数a和b,规定a☆b=ab2+2ab+a,如:1☆3=1×32+2×1×3+1=16.(1)、求(-2)☆3的值;(2)、若( ☆3)☆ =8,求a的值;(3)、若2☆x=m, ☆3=n(其中x为有理数),写出m,n的大小.25. 用“⊗”定义一种新运算:对于任何有理数x和y,规定x⊗y= .(1)、求2⊗(﹣3)的值;(2)、若(﹣a2)⊗2=m,求m的最大整数;(3)、若关于n的方程满足:1⊗n=﹣n﹣2,求n的值;(4)、若 , t3+2t2+3t+1,且A⊗B=﹣2,求5+12t﹣2t3的值.26. 对于有理数a,b,定义了一种新运算“※”为: , 如:5※3=2×5﹣3=7, .(1)、计算:①2※(﹣1)= ;②(-4)※(﹣3)=;(2)、若3※m=﹣1+3x是关于x的一元一次方程,且方程的解为x=2,求m的值;(3)、若A<B,A=﹣x3+4x2﹣x+1,B=﹣x3+6x2﹣x+2,且A※B=﹣3,求2x3+2x的值.27. 阅读下列材料,并解决下面的问题:
表示的运算,并计算结果. 22. 已知x,y为有理数,现规定一种新运算“”,满足 .(1)、求的值;(2)、记 , , 请猜想P与Q的数量关系,并说明理由.23. 设为实数,则我们把形如的式子叫做二阶行列式,它的运算法则用公式表示为 , 请利用此法则解决以下问题:(1)、求的值;(2)、若 , 求的值.24. 用“☆”定义一种新运算:对于任意有理数a和b,规定a☆b=ab2+2ab+a,如:1☆3=1×32+2×1×3+1=16.(1)、求(-2)☆3的值;(2)、若( ☆3)☆ =8,求a的值;(3)、若2☆x=m, ☆3=n(其中x为有理数),写出m,n的大小.25. 用“⊗”定义一种新运算:对于任何有理数x和y,规定x⊗y= .(1)、求2⊗(﹣3)的值;(2)、若(﹣a2)⊗2=m,求m的最大整数;(3)、若关于n的方程满足:1⊗n=﹣n﹣2,求n的值;(4)、若 , t3+2t2+3t+1,且A⊗B=﹣2,求5+12t﹣2t3的值.26. 对于有理数a,b,定义了一种新运算“※”为: , 如:5※3=2×5﹣3=7, .(1)、计算:①2※(﹣1)= ;②(-4)※(﹣3)=;(2)、若3※m=﹣1+3x是关于x的一元一次方程,且方程的解为x=2,求m的值;(3)、若A<B,A=﹣x3+4x2﹣x+1,B=﹣x3+6x2﹣x+2,且A※B=﹣3,求2x3+2x的值.27. 阅读下列材料,并解决下面的问题:我们知道,加减运算是互逆运算,乘除运算也是互逆运算,其实乘方运算也有逆运算,如我们规定式子可以变形为也可以变形为.在式子中,3叫做以2为底8的对数,记为一般地,若则叫做以为底的对数,记为且具有性质:
其中且
根据上面的规定,请解决下面问题:
(1)、计算:; (请直接写出结果);(2)、已知请你用含的代数式来表示其中(请写出必要的过程).28. 对于数轴上的两点P , Q给出如下定义:P , Q两点到原点O的距离之差的绝对值称为P , Q两点的友好距离,记为(POQ).例如:P , Q两点表示的数,如图1所示:则(POQ)=|PO﹣QO|=|2﹣1|=1.
 (1)、A , B两点表示的数,如图所示:
(1)、A , B两点表示的数,如图所示: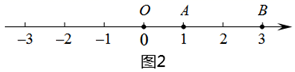
①A , B两点的友好距离为 ▲ ;
②若C为数轴上一点(不与点O重合),且(AOB)=2(AOC),求点C表示的数;
(2)、M , N为数轴上的两点(点M在点N左边),且MN=4,若(MON)=2,直接写出点N表示的数.29. 定义:若 , , 为数轴上三点,若点 到点 的距离是点 到点 的距离2倍,我们就称点 是 的美好点.例如;如图1,点 表示的数为-1,点 表示的数为2.表示1的点 到点 的距离是2,到点 的距离是1,那么点 是 的美好点;又如,表示0的点 到点 的距离是1,到点 的距离是2,那么点 就不是 的美好点,但点 是 的美好点.
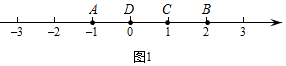
如图2, , 为数轴上两点,点 所表示的数为 ,点 所表示的数为 .
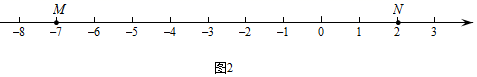
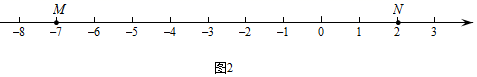 (1)、点 , , 表示的数分别是 , , ,其中是 美好点的是;写出 美好点 所表示的数是 .(2)、现有一只电子蚂蚁 从点 开始出发,以 个单位每秒的速度向左运动.当 为何值时,点 恰好为 的美好点?
(1)、点 , , 表示的数分别是 , , ,其中是 美好点的是;写出 美好点 所表示的数是 .(2)、现有一只电子蚂蚁 从点 开始出发,以 个单位每秒的速度向左运动.当 为何值时,点 恰好为 的美好点?