人教版九年级上对接中考知识点复习专项计划——二次函数的应用之几何问题
试卷更新日期:2022-09-26 类型:复习试卷
一、综合题
-
1. 如图,二次函数 的图象与 轴交于B、C两点(点B在点C的左侧),一次函数 的图象经过点B和二次函数图象上另一点A. 其中点A的坐标为(4 ,3).
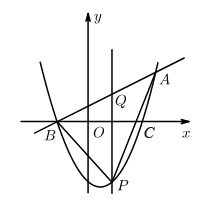 (1)、求二次函数和一次函数的解析式;(2)、若抛物线上的点P在第四象限内,过点P作 轴的垂线PQ,交直线AB于点Q,求线段PQ的最大值.2. 如图,在平面直角坐标系中,点A、C的坐标分别为(-2,0)、(0,-4),点B在x轴上,已知某二次函数的图象经过A、B、C三点,且它的对称轴为直线x=2,点P为直线BC下方的二次函数图象上的一个动点(点P与B、C不重合),过点P作y轴的平行线交BC于点F.
(1)、求二次函数和一次函数的解析式;(2)、若抛物线上的点P在第四象限内,过点P作 轴的垂线PQ,交直线AB于点Q,求线段PQ的最大值.2. 如图,在平面直角坐标系中,点A、C的坐标分别为(-2,0)、(0,-4),点B在x轴上,已知某二次函数的图象经过A、B、C三点,且它的对称轴为直线x=2,点P为直线BC下方的二次函数图象上的一个动点(点P与B、C不重合),过点P作y轴的平行线交BC于点F. (1)、求该二次函数的解析式;(2)、若设点P的横坐标为m,用含m的代数式表示线段PF的长.(3)、求△PBC面积的最大值,并求此时点P的坐标.3. 如图,一个二次函数的图象经过点A(0,1),它的顶点为B(1,3).
(1)、求该二次函数的解析式;(2)、若设点P的横坐标为m,用含m的代数式表示线段PF的长.(3)、求△PBC面积的最大值,并求此时点P的坐标.3. 如图,一个二次函数的图象经过点A(0,1),它的顶点为B(1,3).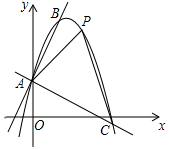 (1)、求这个二次函数的表达式;(2)、过点A作AC⊥AB交抛物线于点C,点P是直线AC上方抛物线上的一点,当△APC面积最大时,求点P的坐标和△APC的面积最大值.4. 如图,二次函数y=ax2+bx+4与y轴交于C点,与x轴交于A、B两点,其中A点坐标为(﹣2,0),B点坐标为(8,0).
(1)、求这个二次函数的表达式;(2)、过点A作AC⊥AB交抛物线于点C,点P是直线AC上方抛物线上的一点,当△APC面积最大时,求点P的坐标和△APC的面积最大值.4. 如图,二次函数y=ax2+bx+4与y轴交于C点,与x轴交于A、B两点,其中A点坐标为(﹣2,0),B点坐标为(8,0).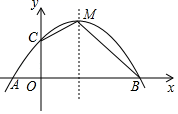 (1)、求经过A,B,C三点的抛物线的解析式;(2)、如果M为抛物线的顶点,连接CM、BM,求四边形COBM的面积.5. 如图是二次函数y=x2+bx+c的图象,其顶点坐标为M(1,-4).
(1)、求经过A,B,C三点的抛物线的解析式;(2)、如果M为抛物线的顶点,连接CM、BM,求四边形COBM的面积.5. 如图是二次函数y=x2+bx+c的图象,其顶点坐标为M(1,-4).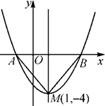 (1)、求出图象与x轴的交点A、B的坐标;(2)、在二次函数的图象上是否存在点P,使S△PAB= S△MAB?若存在,求出点P的坐标;若不存在,请说明理由.6. 如图,已知二次函数的图象经过点A(3,3)、B(4,0)和原点O.P为二次函数图象上的一个动点,过点P作x轴的垂线,垂足为D(m,0),并与直线OA交于点C.
(1)、求出图象与x轴的交点A、B的坐标;(2)、在二次函数的图象上是否存在点P,使S△PAB= S△MAB?若存在,求出点P的坐标;若不存在,请说明理由.6. 如图,已知二次函数的图象经过点A(3,3)、B(4,0)和原点O.P为二次函数图象上的一个动点,过点P作x轴的垂线,垂足为D(m,0),并与直线OA交于点C.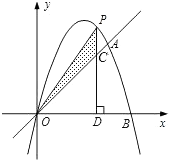
 (1)、求直线OA和二次函数的解析式;(2)、当点P在直线OA的上方时,
(1)、求直线OA和二次函数的解析式;(2)、当点P在直线OA的上方时,①当PC的长最大时,求点P的坐标;
②当S△PCO=S△CDO时,求点P的坐标.
7. 如图,在平面直角坐标系中,经过点的直线AB与y轴交于点 . 经过原点O的抛物线交直线AB于点A,C,抛物线的顶点为D.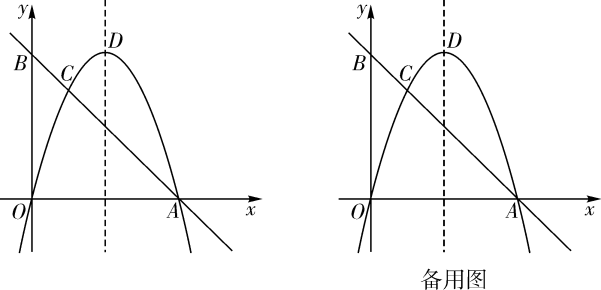 (1)、求抛物线的表达式;(2)、M是线段AB上一点,N是抛物线上一点,当轴且时,求点M的坐标;(3)、P是抛物线上一动点,Q是平面直角坐标系内一点.是否存在以点A,C,P,Q为顶点的四边形是矩形?若存在,直接写出点Q的坐标;若不存在,请说明理由.8. 二次函数y=ax2+bx+4(a≠0)的图象经过点A(-4,0),B(1,0),与y轴交于点C,点P为第二象限内抛物线上一点,连接BP、AC,过点P作PD⊥x轴于点D.
(1)、求抛物线的表达式;(2)、M是线段AB上一点,N是抛物线上一点,当轴且时,求点M的坐标;(3)、P是抛物线上一动点,Q是平面直角坐标系内一点.是否存在以点A,C,P,Q为顶点的四边形是矩形?若存在,直接写出点Q的坐标;若不存在,请说明理由.8. 二次函数y=ax2+bx+4(a≠0)的图象经过点A(-4,0),B(1,0),与y轴交于点C,点P为第二象限内抛物线上一点,连接BP、AC,过点P作PD⊥x轴于点D. (1)、求二次函数的表达式;(2)、连接PA,PC,求的最大值;(3)、连接BC,当∠DPB=2∠BCO时,求直线BP的表达式.9. 如图,已知抛物线y=ax2+bx+3经过点A(﹣1,0)、B(3,0)两点,且交y轴交于点 C.
(1)、求二次函数的表达式;(2)、连接PA,PC,求的最大值;(3)、连接BC,当∠DPB=2∠BCO时,求直线BP的表达式.9. 如图,已知抛物线y=ax2+bx+3经过点A(﹣1,0)、B(3,0)两点,且交y轴交于点 C. (1)、求抛物线的解析式;(2)、点M是线段BC上的点(不与 B、C重合),过M作MN∥y轴交抛物线于N,若点M的横坐标为m,请用m的代数式表示MN的长;(3)、在(2)的条件下,连接NB,NC,是否存在点M,使△BNC的面积最大?若存在,求m的值及△BNC的面积最大值;若不存在,说明理由.10. 如图,已知二次函数图象的顶点在原点,且点(2,1)在二次函数的图象上,过点F(0,1)作x轴的平行线交二次函数的图象于M,N两点
(1)、求抛物线的解析式;(2)、点M是线段BC上的点(不与 B、C重合),过M作MN∥y轴交抛物线于N,若点M的横坐标为m,请用m的代数式表示MN的长;(3)、在(2)的条件下,连接NB,NC,是否存在点M,使△BNC的面积最大?若存在,求m的值及△BNC的面积最大值;若不存在,说明理由.10. 如图,已知二次函数图象的顶点在原点,且点(2,1)在二次函数的图象上,过点F(0,1)作x轴的平行线交二次函数的图象于M,N两点 (1)、求二次函数的表达式;(2)、P为平面内一点,当 时等边三角形时,求点P的坐标;(3)、在二次函数的图象上是否存在一点E,使得以点E为圆心的圆过点F和和点N,且与直线 相切,若存在,求出点E的坐标,并求 的半径;若不存在,说明理由.11. 如图,直线 与x轴交于点B,与y轴交于点C,已知二次函数的图象经过点B、C和点A(-1,0).
(1)、求二次函数的表达式;(2)、P为平面内一点,当 时等边三角形时,求点P的坐标;(3)、在二次函数的图象上是否存在一点E,使得以点E为圆心的圆过点F和和点N,且与直线 相切,若存在,求出点E的坐标,并求 的半径;若不存在,说明理由.11. 如图,直线 与x轴交于点B,与y轴交于点C,已知二次函数的图象经过点B、C和点A(-1,0).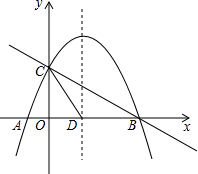 (1)、求B、C两点坐标;(2)、求该二次函数的关系式;(3)、若抛物线的对称轴与x轴的交点为D,点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.(4)、若抛物线的对称轴与x轴的交点为D,则在抛物线在对称轴上是否存在在P,使三角形PCD是以CD为腰在等腰三角形?如果存在,直接写出点P在坐标;如果不存在,请说明理由.12. 二次函数 的图象,与 轴交于原点和点 ,顶点 的坐标为 .
(1)、求B、C两点坐标;(2)、求该二次函数的关系式;(3)、若抛物线的对称轴与x轴的交点为D,点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.(4)、若抛物线的对称轴与x轴的交点为D,则在抛物线在对称轴上是否存在在P,使三角形PCD是以CD为腰在等腰三角形?如果存在,直接写出点P在坐标;如果不存在,请说明理由.12. 二次函数 的图象,与 轴交于原点和点 ,顶点 的坐标为 .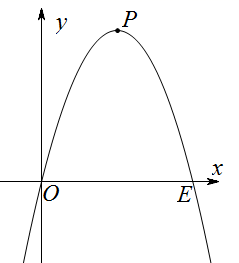 (1)、求二次函数的表达式;(2)、大家知道二次函数的图象是一条抛物线,过 两点可以画无数条抛物线,设顶点为 ,过点 向 轴、 轴作垂线,垂足为点 .求当所得的四边形 为正方形时的二次函数表达式;(3)、 点在(1)中求出的二次函数图象上,且 点的横坐标为1, 点是坐标平面上一点,点 在 轴上,是否存在以 四点为顶点的四边形是正方形,若存在,求出点 的坐标;若不存在,说明理由.13. 已知二次函数y=ax2+2x+c(a≠0)的图象与x轴交于A、B(1,0)两点,与y轴交于点C(0,﹣3),
(1)、求二次函数的表达式;(2)、大家知道二次函数的图象是一条抛物线,过 两点可以画无数条抛物线,设顶点为 ,过点 向 轴、 轴作垂线,垂足为点 .求当所得的四边形 为正方形时的二次函数表达式;(3)、 点在(1)中求出的二次函数图象上,且 点的横坐标为1, 点是坐标平面上一点,点 在 轴上,是否存在以 四点为顶点的四边形是正方形,若存在,求出点 的坐标;若不存在,说明理由.13. 已知二次函数y=ax2+2x+c(a≠0)的图象与x轴交于A、B(1,0)两点,与y轴交于点C(0,﹣3),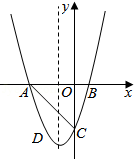 (1)、求二次函数的表达式(2)、D是二次函数图象上位于第三象限内的点,求使△ADC面积最大时点D的坐标;(3)、M是二次函数图象对称轴上的点,在二次函数图象上是否存在点N,使以M、N、B、O为顶点的四边形是平行四边形?若有,请直接写出点N的坐标14. 已知:二次函数y=ax2+bx+c的图象的顶点为(-1,4),与x轴交于A,B两点,与y轴交于点C(0,3),如图.
(1)、求二次函数的表达式(2)、D是二次函数图象上位于第三象限内的点,求使△ADC面积最大时点D的坐标;(3)、M是二次函数图象对称轴上的点,在二次函数图象上是否存在点N,使以M、N、B、O为顶点的四边形是平行四边形?若有,请直接写出点N的坐标14. 已知:二次函数y=ax2+bx+c的图象的顶点为(-1,4),与x轴交于A,B两点,与y轴交于点C(0,3),如图.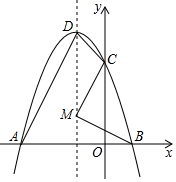 (1)、求二次函数的表达式;(2)、在抛物线的对称轴上有一点M,使得△BCM的周长最小,求出点M的坐标;(3)、若点Q在抛物线的对称轴上,抛物线上是否存在点P,使得以A、B、Q、P四点为顶点的四边形为平行四边形?若存在,求出满足条件的点P的坐标;若不存在,请说明理由.15. 如图,已知二次函数 的图象分别交 轴于点 , ,交 轴于点 ,抛物线的顶点为 ,其中点 , , .
(1)、求二次函数的表达式;(2)、在抛物线的对称轴上有一点M,使得△BCM的周长最小,求出点M的坐标;(3)、若点Q在抛物线的对称轴上,抛物线上是否存在点P,使得以A、B、Q、P四点为顶点的四边形为平行四边形?若存在,求出满足条件的点P的坐标;若不存在,请说明理由.15. 如图,已知二次函数 的图象分别交 轴于点 , ,交 轴于点 ,抛物线的顶点为 ,其中点 , , .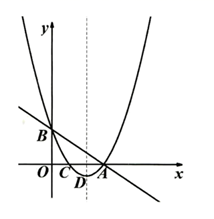 (1)、求抛物线的解析式并直接写出抛物线的对称轴;(2)、在直线 的上方抛物线上有一点 ,且满足 ,请求出点 的坐标;(3)、点 为对称轴上一点,点 为抛物线上一点,是否存在点 , ,使以点A,B,M,N为顶点的四边形是平行四边形?若存在请直接写出点 的坐标,若不存在请说明理由.16. 如图,对称轴为直线 的二次函数 的图象与x轴交于A、B两点,与y轴交于C点,B点的坐标为(1,0).
(1)、求抛物线的解析式并直接写出抛物线的对称轴;(2)、在直线 的上方抛物线上有一点 ,且满足 ,请求出点 的坐标;(3)、点 为对称轴上一点,点 为抛物线上一点,是否存在点 , ,使以点A,B,M,N为顶点的四边形是平行四边形?若存在请直接写出点 的坐标,若不存在请说明理由.16. 如图,对称轴为直线 的二次函数 的图象与x轴交于A、B两点,与y轴交于C点,B点的坐标为(1,0).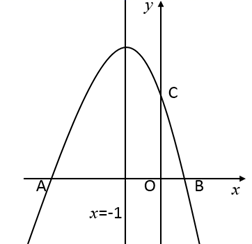 (1)、求此二次函数的解析式;(2)、在直线 上找一点P,使 PBC的周长最小,并求出点P的坐标;(3)、若第二象限的且横坐标为t的点Q在此二次函数的图象上,则当t为何值时,四边形AQCB的面积最大?最大面积是多少?17. 已知二次函数 的图象与x轴交于 两点,与y轴交于点 ,
(1)、求此二次函数的解析式;(2)、在直线 上找一点P,使 PBC的周长最小,并求出点P的坐标;(3)、若第二象限的且横坐标为t的点Q在此二次函数的图象上,则当t为何值时,四边形AQCB的面积最大?最大面积是多少?17. 已知二次函数 的图象与x轴交于 两点,与y轴交于点 ,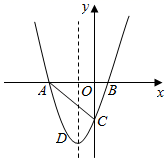 (1)、求二次函数的表达式及A点坐标;(2)、D是二次函数图象上位于第三象限内的点,求点D到直线 的距离取得最大值时点D的坐标;(3)、M是二次函数图象对称轴上的点,在二次函数图象上是否存在点N.使以 为顶点的四边形是平行四边形?若有,请写出点N的坐标(不写求解过程).18. 已知:如图,二次函数 的图象与 轴交于 、 两点,其中 点坐标为 ,点 ,另抛物线经过点 , 为它的顶点.
(1)、求二次函数的表达式及A点坐标;(2)、D是二次函数图象上位于第三象限内的点,求点D到直线 的距离取得最大值时点D的坐标;(3)、M是二次函数图象对称轴上的点,在二次函数图象上是否存在点N.使以 为顶点的四边形是平行四边形?若有,请写出点N的坐标(不写求解过程).18. 已知:如图,二次函数 的图象与 轴交于 、 两点,其中 点坐标为 ,点 ,另抛物线经过点 , 为它的顶点.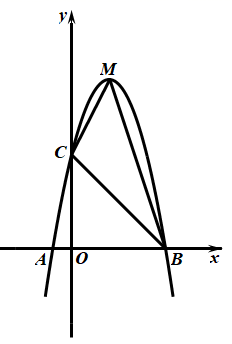 (1)、求抛物线的解析式;(2)、求 的面积 .(3)、是否存在在抛物线上的点 使得 的面积为15,如果存在求出 点的坐标,若不存在请说明理由.19. 二次函数y=-x2+bx+c的图像与x轴交于点B(-3,0),与y轴交于点C(0,-3)。
(1)、求抛物线的解析式;(2)、求 的面积 .(3)、是否存在在抛物线上的点 使得 的面积为15,如果存在求出 点的坐标,若不存在请说明理由.19. 二次函数y=-x2+bx+c的图像与x轴交于点B(-3,0),与y轴交于点C(0,-3)。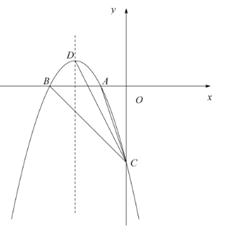 (1)、求二次函数解析式;(2)、设抛物线的顶点为D,与x轴的另一个交点为A,点P在抛物线的对称轴上,且∠APD=∠ACB,求点P的坐标;(3)、连接CD,求∠OCA与∠OCD的两个角的和的度数。20. 如图,已知二次函数y=ax2+bx+3 的图象与x轴分别交于A(1,0),B(3,0)两点,与y轴交于点C
(1)、求二次函数解析式;(2)、设抛物线的顶点为D,与x轴的另一个交点为A,点P在抛物线的对称轴上,且∠APD=∠ACB,求点P的坐标;(3)、连接CD,求∠OCA与∠OCD的两个角的和的度数。20. 如图,已知二次函数y=ax2+bx+3 的图象与x轴分别交于A(1,0),B(3,0)两点,与y轴交于点C (1)、求此二次函数解析式;(2)、点D为抛物线的顶点,试判断△BCD的形状,并说明理由;(3)、将直线BC向上平移t(t>0)个单位,平移后的直线与抛物线交于M,N两点(点M在y轴的右侧),当△AMN为直角三角形时,求t的值.21. 如图,直线y=- x+2与x轴交于点B,与y轴交于点C,已知二次函数的图象经过点B,C和点A(-1,0).
(1)、求此二次函数解析式;(2)、点D为抛物线的顶点,试判断△BCD的形状,并说明理由;(3)、将直线BC向上平移t(t>0)个单位,平移后的直线与抛物线交于M,N两点(点M在y轴的右侧),当△AMN为直角三角形时,求t的值.21. 如图,直线y=- x+2与x轴交于点B,与y轴交于点C,已知二次函数的图象经过点B,C和点A(-1,0).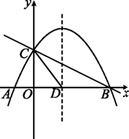 (1)、求B,C两点的坐标.(2)、求该二次函数的解析式.(3)、若抛物线的对称轴与x轴的交点为点D,则在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出点P的坐标;如果不存在,请说明理由.(4)、点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时点E的坐标.22. 如图,二次函数y=ax2+bx+c的图象经过点(-1,4),且与直线y=- x+1相交于A,B两点,A点在y轴上,过点B作BC⊥x轴,垂足为点C(-3,0).
(1)、求B,C两点的坐标.(2)、求该二次函数的解析式.(3)、若抛物线的对称轴与x轴的交点为点D,则在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出点P的坐标;如果不存在,请说明理由.(4)、点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时点E的坐标.22. 如图,二次函数y=ax2+bx+c的图象经过点(-1,4),且与直线y=- x+1相交于A,B两点,A点在y轴上,过点B作BC⊥x轴,垂足为点C(-3,0).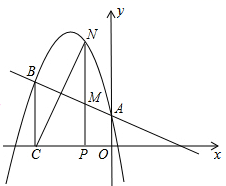 (1)、求二次函数的表达式;(2)、点N是二次函数图象上一点(点N在AB上方),过N作NP⊥x轴,垂足为点P,交AB于点M,求MN的最大值;(3)、在(2)的条件下,点N在何位置时,四边形BCMN是平行四边形?并求出满足条件的N点的坐标.23. 如图,已知二次函数 ( )的图象与 轴交于 , 两点(点 在点 的左侧),与 轴交于点 ,横坐标分别为 , ( )的 、 两点在线段 上(不与 、 重合),过 、 两点作 轴的垂线分别交抛物线于点 、 ,连接 .
(1)、求二次函数的表达式;(2)、点N是二次函数图象上一点(点N在AB上方),过N作NP⊥x轴,垂足为点P,交AB于点M,求MN的最大值;(3)、在(2)的条件下,点N在何位置时,四边形BCMN是平行四边形?并求出满足条件的N点的坐标.23. 如图,已知二次函数 ( )的图象与 轴交于 , 两点(点 在点 的左侧),与 轴交于点 ,横坐标分别为 , ( )的 、 两点在线段 上(不与 、 重合),过 、 两点作 轴的垂线分别交抛物线于点 、 ,连接 .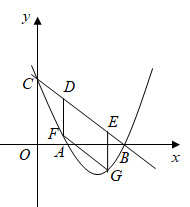 (1)、求线段 的值.(2)、若四边形 是平行四边形;
(1)、求线段 的值.(2)、若四边形 是平行四边形;①点 、 横坐标之和是否为定值,若是定值,请求出;若不是,请说明理由.
②当 时,平行四边形 能否为菱形;若能,求出菱形的周长:若不能,请说明理由.
24. 如图,二次函数 的图象交x轴于点 , ,交y轴于点C.点 是x轴上的一动点, 轴,交直线 于点M,交抛物线于点N. (1)、求这个二次函数的表达式;(2)、①若点P仅在线段 上运动,如图1.求线段 的最大值;
(1)、求这个二次函数的表达式;(2)、①若点P仅在线段 上运动,如图1.求线段 的最大值;②若点P在x轴上运动,则在y轴上是否存在点Q,使以M,N,C,Q为顶点的四边形为菱形.若存在,请直接写出所有满足条件的点Q的坐标;若不存在,请说明理由.
25. 如图,二次函数y=ax²+bx+c(a≠0)的图象交x轴于A、B两点,交y轴于点D,点B的坐标为(3,0),顶点C的坐标为(1,4)。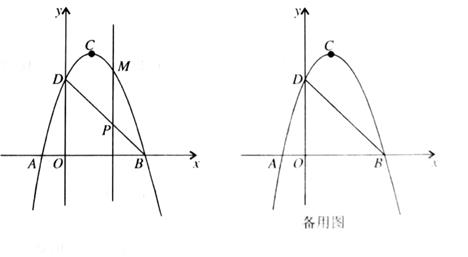 (1)、求二次函数的解析式和直线BD的解析式;(2)、点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;
(1)、求二次函数的解析式和直线BD的解析式;(2)、点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;
(3)、在抛物线上是否存在异于B、D的点Q,使△BDQ中BD边上的高为2 ?若存在求出点Q的坐标;若不存在请说明理由。
26. 如图,二次函数y=﹣2x2+x+m的图象与x轴的一个交点为A(1,0),另一个交点为B,且与y轴交于点C.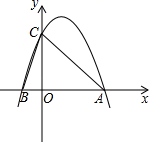 (1)、求m的值;(2)、求点B的坐标;(3)、该二次函数图象上是否有一点D(x,y)使S△ABD=S△ABC , 求点D的坐标.27. 如图①,二次函数 的图像与 轴交于 、 两点(点 在 的左侧),顶点为 ,连接 并延长交 轴于点 ,若 .
(1)、求m的值;(2)、求点B的坐标;(3)、该二次函数图象上是否有一点D(x,y)使S△ABD=S△ABC , 求点D的坐标.27. 如图①,二次函数 的图像与 轴交于 、 两点(点 在 的左侧),顶点为 ,连接 并延长交 轴于点 ,若 .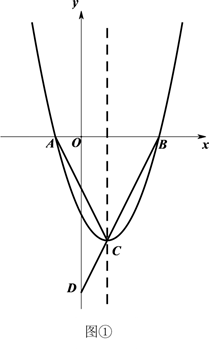
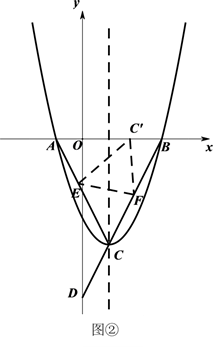 (1)、求二次函数的表达式;(2)、在 轴上方有一点 , ,且 ,连接 并延长交抛物线于点 ,求点 的坐标;(3)、如图②,折叠△ ,使点 落在线段 上的点 处,折痕为 .若△ 有一条边与 轴垂直,直接写出此时点 的坐标.28. 已知二次函数 的图象过点 (3,0)、 (-1,0).
(1)、求二次函数的表达式;(2)、在 轴上方有一点 , ,且 ,连接 并延长交抛物线于点 ,求点 的坐标;(3)、如图②,折叠△ ,使点 落在线段 上的点 处,折痕为 .若△ 有一条边与 轴垂直,直接写出此时点 的坐标.28. 已知二次函数 的图象过点 (3,0)、 (-1,0).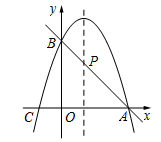 (1)、求二次函数的解析式;(2)、如图,二次函数的图象与 轴交于点 ,二次函数图象的对称轴与直线 交于点 ,求 点的坐标;(3)、在第一象限内的抛物线上有一点 ,当 的面积最大时,求点 的坐标.
(1)、求二次函数的解析式;(2)、如图,二次函数的图象与 轴交于点 ,二次函数图象的对称轴与直线 交于点 ,求 点的坐标;(3)、在第一象限内的抛物线上有一点 ,当 的面积最大时,求点 的坐标.