2022-2023学年苏科版数学七上尖子生考点培优专题训练2 探索图形的规律
试卷更新日期：2022-09-26 类型：复习试卷
一、单选题
-
1. 为庆祝“六一”儿童节，某幼儿园举行用火柴棒摆“金鱼”比赛，如图所示.
按以上的规律，第n个“金鱼”需用火柴棒的根数为（ ）
A、 B、 C、 D、2. 如图是一组有规律的图案，它们是由边长相同的黑白两种颜色的小正方形组成的，按照这样的规律，若组成的图案中有2021个黑色小正方形，则这个图案是（ ）
A、第505个 B、第506个 C、第507个 D、第508个3. 下列图形都是由同样大小的小圆圈按一定规律所组成的，其中第①个图形中一共有4个小圆圈，第②个图形中一共有10个小圆圈，第③个图形中一共有19个小圆圈，…，按此规律排列，则第⑥个图形中小圆圈的个数为（ ）
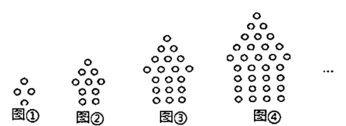A、31 B、46 C、64 D、854. 如图所示，把同样大小的黑色棋子分别摆放在正多边形（正三角形、正四边形、正五边形、正六边形…）的边上，按照这样的规律继续摆放下去…，则第5个图形需要黑色棋子的个数是 （ ）
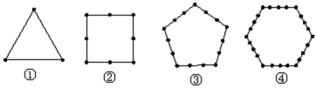A、30 B、33 C、35 D、425. 搭建如图①的单顶帐篷需要17根钢管，这样的帐篷按图②、图③的方式串起来搭建，则搭建7顶这样的帐篷需要（ ）根钢管．
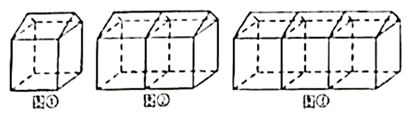A、83 B、94 C、102 D、1196. 如图是一组有规律的图案，它们由边长相等的等边三角形组合而成，第1个图案有4个三角形，第2个图案有7个三角形，第3个图案有10个三角形，…，照此规律，摆成第个图案需要的三角形个数是（ ）
A、个 B、个 C、个 D、个7. 将一些半径相同的小圆按如图所示的规律摆放，请仔细观察，第n个图形的小圆个数是（ ）（用含有n的代数式表示）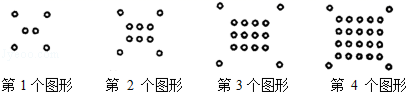
A、4n+（n+1） B、n2+4n C、4+n（n+1） D、4+（n+1）28. 如图（1）是一个三角形，分别连接这个三角形三边中点得到图（2），再分别连接图（2）中间的小三角形三边中点得到图（3），按这种方法继续下去，第6个图形有（ ）个三角形．
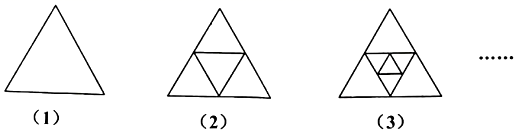A、20 B、21 C、22 D、239. 观察如图图形，它们是按一定规律排列的，依照此规律，第9个图形中的小点一共有（ ）
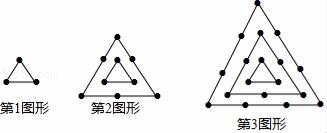A、162个 B、135个 C、30个 D、27个10. 如图所示，将形状、大小完全相同的“●”和线段按照一定规律摆成下列图形，第1幅图形中“●”的个数为a1 ， 第2幅图形中“●”的个数为a2 ， 第3幅图形中“●”的个数为a3 ， …，以此类推，则+++…+的值为（ ）
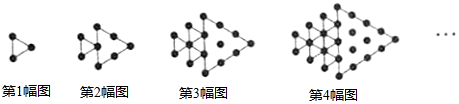A、 B、 C、 D、二、填空题
-
11. 如图，自左向右水平摆放一组小球，按照以下规律排列：红球、黄球、绿球、红球、黄球、绿球……小王依次在小球上标上数字1，2，3，4，5，6，…….若某个小球上标的数字是2022，则这个小球的颜色是.
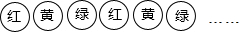12. 观察下列图形的构成规律，按此规律，第20个图形中棋子的个数为 ．
13. 将黑色圆点按如图所示的规律进行排列：
图中黑色圆点的个数依次为：1，3，6，10，……，将其中所有能被3整除的数按从小到大的顺序重新排列成一组新数据，则新数据中的第10个数为 ， 第55个数为.
14. 如图是一组有规律的图案，它们是由边长相等的正方形组合而成，第1个图案有5个正方形，第2个图案有8个正方形，第3个图案有11个正方形……按此规律摆下去，第n个图案有个正方形（用含n的代数式表示）．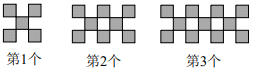
15. 某种杯子的高度是15cm，两个以及三个这样的杯子叠放时高度如图，n个这样的杯子叠放在一起高度是cm（用含n的式子表示）．
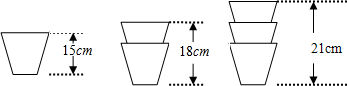16. 一根绳子弯曲成如图1所示的形状.当用剪刀像图2那样沿虚线a把绳子剪断时，绳子被剪为5段；当用剪刀像图3那样沿虚线b(b∥a)把绳子再剪一次时，绳子就被剪为9段.若用剪刀在虚线a，b之间把绳子再剪(n﹣2)次(剪刀的方向与a平行)，这样一共剪n次时绳子的段数是.
17. 将正整数从1开始按如图所示的规律排成一个数阵.其中，2在第一个拐弯处，3在第二个拐弯处，5在第三个拐弯处，7在第四个拐弯处，…，则第50个拐弯处的数是.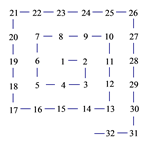
18. 在平面直角坐标系中，若干个边长为1个单位长度的等边三角形，按如图中的规律摆放．点P从原点O出发，以每秒1个单位长度的速度沿着等边三角形的边“OA1→A1A2→A2A3→A3A4→A4A5…”的路线运动，设第n秒运动到点Pn（n为正整数），则点P2020的坐标是 ．
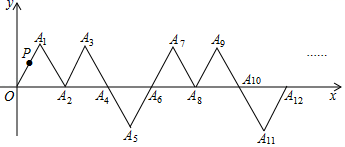19. 如图，平面内有公共端点的六条射线，OB，OC，OD，OE，OF，从射线OA开始按逆时针方向依次在射线上写出数字1，2，3，4，5，6，7，….则“2021”在射线 上.
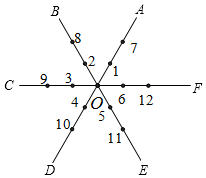20. 如图，把一个面积为1的正方形等分成两个面积为 的矩形，接着把其中一个面积为 的矩形等分成两个面积为 的矩形，再把其中一个面积为 的矩形等分成两个面积为 的矩形，如此进行下去，试利用图形所揭示的规律计算： ．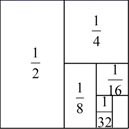
三、解答题
-
21. 如图所示，由一些点组成形如三角形的图形，每条“边”（包括两个顶点）有 个点，每个图形的总点数记为S ．
(1)、当 时，S的值为；当 时，S的值为；(2)、每条“边”有n个点时的总点数S是（用含n的式子表示）；(3)、当 时，总点数S是多少？22. 如图，每张小纸带的长为30cm，宽为10cm，用胶水把它们粘贴成一张长纸带，接头部分的长为3cm.
(1)、用2张这样的小纸条粘贴成的纸带的长度为57cm，则用3张这样的小纸条粘贴成的纸带的长度为cm.(2)、用n张这样的小纸带粘贴成的纸带的长度是cm.(3)、若粘贴成的纸带的长度为408cm，则需要多少张长为30cm，宽为10cm的小纸带？23. 图1是一个三角形，分别连接这个三角形三边的中点得到图2；再分别连接图2中间小角形三边的中点，得到图3.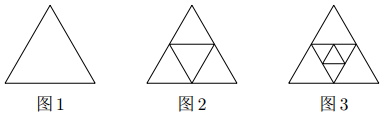
(1)、图2中共有个三角形，图3中共有三角形；(2)、按上面的方法继续下去：①第n个图形（图1是第一个图形）中共有多少个三角形（用含n的代数式表示）？如果某个图形有2021个三角形，求n的值.
②是否存在相邻两个图形的三角形的数量之和等于另一个图形的三角形的数量？说明理由.
24. 用棋子摆出下列一组图形：
(1)、填写下表：图形编号
1
2
3
4
5
6
图形中的棋子
6
(2)、照这样的方式摆下去，写出摆第 n 个图形棋子的枚数；(3)、如果某一图形共有99枚棋子，你知道它是第几个图形吗？25. 学校餐厅中，一张桌子可坐6人，有以下两种摆放方式：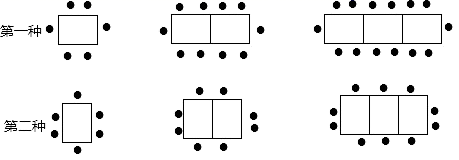
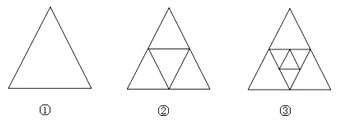
(1)、当有5张桌子时，两种摆放方式各能坐多少人？(2)、当有n张桌子时，两种摆放方式各能坐多少人？(3)、新学期有200人在学校就餐，但餐厅只有60张这样的餐桌，若你是老师，你打算选择哪种方式来摆放餐桌？为什么？26.图①是一个三角形，分别连接这个三角形三边的中点得到图②，再分别连接图②中间小三角形三边的中点，得到图③．
（1）图②有多少个三角形；图③有多少个三角形．
（2）按上面的方法继续下去，第n个图形中有多少个三角形？（用n的代数式表示结论）
（3）有没有一个图形中存在2016个三角形？如果存在，请求出是第几个三角形；如果不存在，请说明理由．
27. 小丽在用等长的木棒设计图案，她先用 根木棒摆成图案①，再按图案①的个数逐渐增加 的规律拼成下图中的图案②和图案③.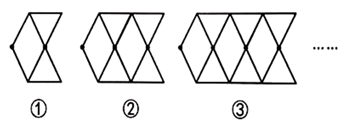
(1)、她在摆第 个图案时，用了多少根木棒？(2)、请你帮她用含 的代数式表示第 个图案所需木棒的根数.(3)、如果要摆出第 个图案，所需木棒的根数是多少？28. 如图是用大小相等的小五角星按一定规律拼成的一组图案，第1个图案中有4颗五角星，第2个图案中有7颗五角星，第3个图案中有10颗五角星，…，请根据你的观察完成下列问题．
(1)、根据上述规律，分别写出第4个图案和第5个图案中小五角星的颗数；(2)、按如图所示的规律，直接写出第 个图案中小五角星的颗数；（用含 的代数式表示）(3)、第2021个图案中有多少颗五角星？29. 用同样大小的两种不同颜色的正方形纸片，按下图方式拼正方形.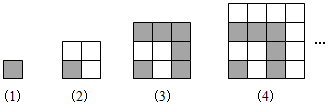
第（1）个图形中有1个正方形；
第（2）个图形有1+3＝4个小正方形；
第（3）个图形有1+3+5＝9个小正方形；
第（4）个图形有1+3+5+7＝16小正方形；
……
(1)、根据上面的发现我们可以猜想：1+3+5+7+…+（2n﹣1）＝（用含n的代数式表示）；(2)、请根据你的发现计算：①1+3+5+7+…+79；
②81+83+85+…+399.
30. 如图1是由若干个小圆圈堆成的一个形如正三角形的图案，最上面一层有一个圆圈，以下各层均比上一层多一个圆圈，一共堆了n层.将图1倒置后与原图1拼成图2的形状，这样我们可以算出图1中所有圆圈的个数为 .
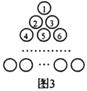
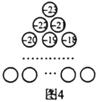
如果图1中的圆圈共有12层，
(1)、我们自上往下，在每个圆圈中都按图3的方式填上一串连续的正整数1，2，3，4，…，则最底层最左边这个圆圈中的数是；(2)、我们自上往下，在每个圆圈中都按图4的方式填上一串连续的整数-23，-22，-21，…，求图4中所有圆圈中各数的绝对值之和.