四川省巴中市2022-2023学年高三上学期理数零诊考试试卷
试卷更新日期:2022-09-26 类型:高考模拟
一、单选题
-
1. 设全集 , 若集合满足 . 则( )A、 B、 C、 D、2. 若复数满足(为虚数单位),则复数的虚部为( )A、 B、 C、3 D、-33. 已知直线: , : , 则“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件4. 已知双曲线的焦点到渐近线的距离为2,则该双曲线的离心率为( )A、 B、 C、 D、5. 已知 , 是两个不同的平面, , 是两条不重合的直线,则下列命题中正确的是( )A、若 , , 则 B、若 , , , 则 C、若 , , , 则 D、若 , , , 则6. 已知角的顶点在坐标原点,始边与轴的非负半轴重合,终边上有两点 , 且 , 则( )A、 B、4 C、 D、7. 函数在区间上的图象为( )A、
 B、
B、 C、
C、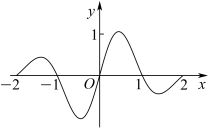 D、
D、 8. 已知等差数列的前项和为 , 若 , 且 , 则( )A、0 B、1 C、2022 D、20239. 已知点在直角的斜边上,若 , , 则的取值范围为( )A、 B、 C、 D、10. 设 , 若函数的图象向左平移个单位长度后与函数的图象重合,则的最小值为( )A、 B、 C、 D、11. 已知定义在上的函数满足 , 当时, . 若对任意 , 都有 , 则的取值范围是( )A、 B、 C、 D、12. 已知 , , , 则( )A、 B、 C、 D、
8. 已知等差数列的前项和为 , 若 , 且 , 则( )A、0 B、1 C、2022 D、20239. 已知点在直角的斜边上,若 , , 则的取值范围为( )A、 B、 C、 D、10. 设 , 若函数的图象向左平移个单位长度后与函数的图象重合,则的最小值为( )A、 B、 C、 D、11. 已知定义在上的函数满足 , 当时, . 若对任意 , 都有 , 则的取值范围是( )A、 B、 C、 D、12. 已知 , , , 则( )A、 B、 C、 D、二、填空题
-
13. 已知 , 若 , 则 .14. 某智能机器人的广告费用(万元)与销售额(万元)的统计数据如下表:
广告费用(万元)
2
3
5
6
销售额(万元)
28
31
41
48
根据上表可得回归方程 , 据此模型预报广告费用为8万元时销售额为万元.
15. 在三棱锥中,平面 , , , , 则三棱锥的外接球的体积为 .三、双空题
-
16. 在锐角中,角 , , 的对边分别为 , , , 若 , 则 , 的取值范围为 .
四、解答题
-
17. 已知数列的前项和为 , 若 , 且 .(1)、求数列的通项公式;(2)、若数列满足 , 求数列的前项和 .18. 自《“健康中国2030”规划纲要》颁布实施以来,越来越多的市民加入到绿色运动“健步走”行列以提高自身的健康水平与身体素质.某调查小组为了解本市不同年龄段的市民在一周内健步走的情况,在市民中随机抽取了200人进行调查,部分结果如下表所示,其中一周内健步走少于5万步的人数占样本总数的 , 45岁以上(含45岁)的人数占样本总数的 .
一周内健步走万步
一周内健步走<5万步
总计
45岁以上(含45岁)
90
45岁以下
总计
附:
0.150
0.100
0.050
0.025
2.072
2.706
3.841
5.024
, 其中 .
(1)、请将题中表格补充完整,并判断是否有90%的把握认为该市市民一周内健步走的步数与年龄有关;(2)、现从样本中45岁以上(含45岁)的人群中按一周内健步走的步数是否少于5万步用分层抽样法抽取8人做进一步访谈,然后从这8人中随机抽取2人填写调查问卷,记抽取的两人中一周内健步走步数不少于5万步的人数为 , 求的分布列及数学期望.19. 如图,正方形和直角梯形所在平面互相垂直, , , 且 , .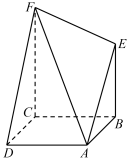 (1)、证明:平面;(2)、求二面角的余弦值.20. 已知椭圆:的左、右顶点分别为、 , 点在椭圆上,且直线的斜率与直线的斜率之积为 .(1)、求椭圆的方程;(2)、若圆的切线与椭圆交于、两点,求的最大值及此时直线的斜率.
(1)、证明:平面;(2)、求二面角的余弦值.20. 已知椭圆:的左、右顶点分别为、 , 点在椭圆上,且直线的斜率与直线的斜率之积为 .(1)、求椭圆的方程;(2)、若圆的切线与椭圆交于、两点,求的最大值及此时直线的斜率.
-