山东省济南市2022-2023学年高三上学期数学9月摸底考试试卷
试卷更新日期:2022-09-26 类型:月考试卷
一、单选题
-
1. 设集合 , , 则( )A、 B、 C、 D、2. 命题“”的否定为( )A、 B、 C、 D、3. 已知(其中为虚数单位),则复数( )A、 B、 C、 D、4. 已知函数的最小正周期为 , 则的图象关于( )A、对称 B、对称 C、对称 D、对称5. 拟柱体(所有顶点均在两个平行平面内的多面体)可以用辛普森(Simpson)公式求体积,其中是高,是上底面面积,是下底面面积,是中截面(到上、下底面距离相等的截面)面积.如图所示,在五面体中,底面是边长为2的正方形, , 且直线到底面的距离为2,则该五面体的体积为( )
 A、 B、 C、3 D、6. 已知双曲线的离心率为分别为的左、右焦点,过的直线与的左支交于两点,若的最小值为4,则周长的最小值为( )A、8 B、12 C、16 D、247. 从装有个红球和个蓝球的袋中( , 均不小于2),每次不放回地随机摸出一球.记“第一次摸球时摸到红球”为 , “第一次摸球时摸到蓝球”为;“第二次摸球时摸到红球”为 , “第二次摸球时摸到蓝球”为 , 则下列说法错误的是( )A、 B、 C、 D、8. 定义在上的函数满足 , , 当时, , 则方程在上解的个数为( )A、3 B、4 C、5 D、6
A、 B、 C、3 D、6. 已知双曲线的离心率为分别为的左、右焦点,过的直线与的左支交于两点,若的最小值为4,则周长的最小值为( )A、8 B、12 C、16 D、247. 从装有个红球和个蓝球的袋中( , 均不小于2),每次不放回地随机摸出一球.记“第一次摸球时摸到红球”为 , “第一次摸球时摸到蓝球”为;“第二次摸球时摸到红球”为 , “第二次摸球时摸到蓝球”为 , 则下列说法错误的是( )A、 B、 C、 D、8. 定义在上的函数满足 , , 当时, , 则方程在上解的个数为( )A、3 B、4 C、5 D、6二、多选题
-
9. 下图为2022年8月5日通报的14天内31省区市疫情趋势,则下列说法正确的是( )
 A、无症状感染者的极差大于 B、确诊病例的方差大于无症状感染者的方差 C、实际新增感染者的平均数小于 D、实际新增感染者的第80百分位数为64110. 如图所示,在正六边形中,下列说法正确的是( )
A、无症状感染者的极差大于 B、确诊病例的方差大于无症状感染者的方差 C、实际新增感染者的平均数小于 D、实际新增感染者的第80百分位数为64110. 如图所示,在正六边形中,下列说法正确的是( ) A、 B、 C、 D、在上的投影向量为11. 如图所示,设单位圆与轴的正半轴相交于点 , 以轴非负半轴为始边作锐角 , , , 它们的终边分别与单位圆相交于点 , , , 则下列说法正确的是( )
A、 B、 C、 D、在上的投影向量为11. 如图所示,设单位圆与轴的正半轴相交于点 , 以轴非负半轴为始边作锐角 , , , 它们的终边分别与单位圆相交于点 , , , 则下列说法正确的是( )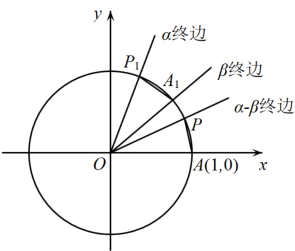 A、的长度为 B、扇形的面积为 C、当与重合时, D、当时,四边形面积的最大值为12. 在正四面体中,若 , 则下列说法正确的是( )A、该四面体外接球的表面积为 B、直线与平面所成角的正弦值为 C、如果点在上,则的最小值为 D、过线段一个三等分点且与垂直的平面截该四面体所得截面的周长为
A、的长度为 B、扇形的面积为 C、当与重合时, D、当时,四边形面积的最大值为12. 在正四面体中,若 , 则下列说法正确的是( )A、该四面体外接球的表面积为 B、直线与平面所成角的正弦值为 C、如果点在上,则的最小值为 D、过线段一个三等分点且与垂直的平面截该四面体所得截面的周长为三、双空题
-
13. 使命题“若 , 则”为假命题的一组 , 的值分别为 , .
四、填空题
-
14. 的展开式中,含项的系数为(用数字作答).15. 过点的直线与圆交于 , 两点,则的值为.16. 定义在上的可导函数满足 , 且在上有成立.若实数满足 , 则的取值范围是 .
五、解答题
-
17. 在中,边上的中线长为.(1)、求的值;
 (2)、求的面积.18. 为庆祝中国共产主义青年团成立100周年,某校团委组织团员参加知识竞赛.根据成绩,制成如图所示的频率分布直方图.
(2)、求的面积.18. 为庆祝中国共产主义青年团成立100周年,某校团委组织团员参加知识竞赛.根据成绩,制成如图所示的频率分布直方图. (1)、计算的值;(2)、采用按比例分层抽样的方法从成绩在 , 的两组中共抽取7人,再从这7人中随机抽取3人,记为这3人中成绩落在的人数,求的分布列和数学期望.19. 已知正项数列满足 , 且.(1)、求数列的通项公式;(2)、求数列的前项和.
(1)、计算的值;(2)、采用按比例分层抽样的方法从成绩在 , 的两组中共抽取7人,再从这7人中随机抽取3人,记为这3人中成绩落在的人数,求的分布列和数学期望.19. 已知正项数列满足 , 且.(1)、求数列的通项公式;(2)、求数列的前项和.
-
