人教版九年级上对接中考知识点复习专项计划——与二次函数相图像与坐标的交点问题
试卷更新日期:2022-09-26 类型:复习试卷
一、单选题
-
1. 二次函数的图象如图所示,下列结论:;②若为任意实数,则;;;若 , 且 , 则其中正确的个数为( )
 A、2 B、3 C、4 D、52. 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴正半轴相交于A、B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC,则下列结论:①abc>0;②9a+3b+c<0;③c>﹣1;④关于x的方程ax2+bx+c=0(a≠0)有一个根为 , 其中正确结论的个数为( )
A、2 B、3 C、4 D、52. 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴正半轴相交于A、B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC,则下列结论:①abc>0;②9a+3b+c<0;③c>﹣1;④关于x的方程ax2+bx+c=0(a≠0)有一个根为 , 其中正确结论的个数为( ) A、1 B、2 C、3 D、43. 如图是二次函数图象的一部分,对称轴为且经过点下列说法:
A、1 B、2 C、3 D、43. 如图是二次函数图象的一部分,对称轴为且经过点下列说法:;;;若 , 是抛物线上的两点,则;其中其中说法正确的是( )
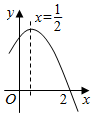 A、 B、 C、 D、4. 已知二次函数下列结论正确是( )
A、 B、 C、 D、4. 已知二次函数下列结论正确是( )①已知点 , 点在二次函数的图象上,则;②该图象一定过定点和;③直线与抛物线一定存在两个交点;④当时,的最小值是 , 则;
A、①④ B、②① C、②④ D、①②③④5. 已知抛物线y=ax2 +bx +c的对称轴为x=1,与x轴正半轴的交点为A(3,0),其部分图象如图所示,有下列结论:①abc >0;②2c﹣3b <0;③5a +b+2c=0;④若B( , y1)、C( , y2)、D( , y3)是抛物线上的三点,则y1<y2<y3.其中正确结论的个数有( )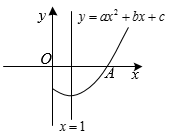 A、1 B、2 C、3 D、46. 如图,已知二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)的图象顶点为P(1,m),经过点A(2,1);有以下结论:①a<0;②abc>0;③4a+2b+c=1;④x>1时,y随x的增大而减小;⑤对于任意实数t,总有at2+bt≤a+b,其中正确的有( )
A、1 B、2 C、3 D、46. 如图,已知二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)的图象顶点为P(1,m),经过点A(2,1);有以下结论:①a<0;②abc>0;③4a+2b+c=1;④x>1时,y随x的增大而减小;⑤对于任意实数t,总有at2+bt≤a+b,其中正确的有( ) A、2个 B、3个 C、4个 D、5个7. 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)abc<0;(2)4a+c>2b;(3)3b﹣2c>0;(4)若点A(﹣2,y1)、点B(﹣ , y2)、点C( , y3)在该函数图象上,则y1<y3<y2;(5)4a+2b≥m(am+b)(m为常数).其中正确的结论有( )
A、2个 B、3个 C、4个 D、5个7. 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)abc<0;(2)4a+c>2b;(3)3b﹣2c>0;(4)若点A(﹣2,y1)、点B(﹣ , y2)、点C( , y3)在该函数图象上,则y1<y3<y2;(5)4a+2b≥m(am+b)(m为常数).其中正确的结论有( )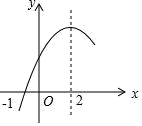 A、5个 B、4个 C、3个 D、2个8. 已知二次函数y=x2−2x−3的自变量x1 , x2 , x3对应的函数值分别为y1 , y2 , y3.当−1<x1<0,1<x2<2,x3>3时,y1 , y2 , y3三者之间的大小关系是( )A、 B、 C、 D、9. 二次函数 的图象如图所示.下列结论:① ;② ;③ 为任意实数,则 ;④ ;⑤若 且 ,则 .其中正确结论的个数有( )
A、5个 B、4个 C、3个 D、2个8. 已知二次函数y=x2−2x−3的自变量x1 , x2 , x3对应的函数值分别为y1 , y2 , y3.当−1<x1<0,1<x2<2,x3>3时,y1 , y2 , y3三者之间的大小关系是( )A、 B、 C、 D、9. 二次函数 的图象如图所示.下列结论:① ;② ;③ 为任意实数,则 ;④ ;⑤若 且 ,则 .其中正确结论的个数有( ) A、1个 B、2个 C、3个 D、4个10. 如图,是二次函数 的图象,图象经过点 ,二次函数的对称轴为 ,给出下列结论: ; ; ; ,其中正确的结论有( )
A、1个 B、2个 C、3个 D、4个10. 如图,是二次函数 的图象,图象经过点 ,二次函数的对称轴为 ,给出下列结论: ; ; ; ,其中正确的结论有( ) A、 B、 C、 D、11. 如图,二次函数的图象开口向上,图象经过点(-1,2)和(1,0),且与轴相交于负半轴.给出四个结论:①;②;③;④ . 其中结论正确的个数为( )
A、 B、 C、 D、11. 如图,二次函数的图象开口向上,图象经过点(-1,2)和(1,0),且与轴相交于负半轴.给出四个结论:①;②;③;④ . 其中结论正确的个数为( ) A、1 B、2 C、3 D、412. 如图,抛物线的对称轴是直线 , 并与轴交于 , 两点,若 , 则下列结论中:;;;若为任意实数,则 , 正确的个数是( )
A、1 B、2 C、3 D、412. 如图,抛物线的对称轴是直线 , 并与轴交于 , 两点,若 , 则下列结论中:;;;若为任意实数,则 , 正确的个数是( )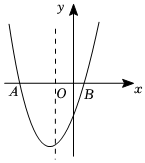 A、1 B、2 C、3 D、413. 如图,已知抛物线 的对称轴是 ,直线 轴,且交抛物线于点 ,下列结论错误的是( )
A、1 B、2 C、3 D、413. 如图,已知抛物线 的对称轴是 ,直线 轴,且交抛物线于点 ,下列结论错误的是( )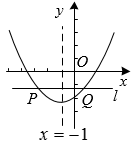 A、 B、若实数 ,则 C、 D、当 时,14. 二次函数 的部分图象如图所示,与y轴交于 ,对称轴为直线 .下列结论:① ;② ;③对于任意实数m,都有 成立;④若 , , 在该函数图象上,则 ;⑤方程 ( ,k为常数)的所有根的和为4.其中正确结论有( )
A、 B、若实数 ,则 C、 D、当 时,14. 二次函数 的部分图象如图所示,与y轴交于 ,对称轴为直线 .下列结论:① ;② ;③对于任意实数m,都有 成立;④若 , , 在该函数图象上,则 ;⑤方程 ( ,k为常数)的所有根的和为4.其中正确结论有( ) A、2 B、3 C、4 D、515. 如图是二次函数图象的y=ax2+bx+c一部分,图象过点A(-3,0),对称轴为直线x=-1。则以下结论错误的是( )
A、2 B、3 C、4 D、515. 如图是二次函数图象的y=ax2+bx+c一部分,图象过点A(-3,0),对称轴为直线x=-1。则以下结论错误的是( ) A、b2>4ac B、2a+b=0 C、a+b+c=0 D、5a<b16. 如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1 , x2如,其中﹣1<x1<0,1<x2<2,下列结论:①4a+2b+c<0;②2a+b>0;③b2+8a>4ac;④a<﹣1.其中结论正确的有( )
A、b2>4ac B、2a+b=0 C、a+b+c=0 D、5a<b16. 如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1 , x2如,其中﹣1<x1<0,1<x2<2,下列结论:①4a+2b+c<0;②2a+b>0;③b2+8a>4ac;④a<﹣1.其中结论正确的有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
17. 如图,抛物线与轴交于点 , 顶点坐标 , 与轴的交点在 , 之间(包含端点),则下列结论正确的有 . ①;②;③对于任意实数 , 恒成立;④关于的方程有两个不相等的实数根.(填编号)
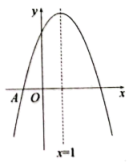 18. 已知二次函数 , 图象的一部分如图所示,该函数图象经过点 , 对称轴为直线.对于下列结论:①;②;③;④(其中);⑤若和均在该函数图象上,且 , 则.其中正确结论的个数共有个.
18. 已知二次函数 , 图象的一部分如图所示,该函数图象经过点 , 对称轴为直线.对于下列结论:①;②;③;④(其中);⑤若和均在该函数图象上,且 , 则.其中正确结论的个数共有个. 19. 关于抛物线 , 与x轴交于A、B两点(A在B左侧),给出下列4个结论:①当抛物线的顶点在y轴的正半轴上时,;②点P在抛物线上,当符合条件(a为常数)的点有3个时,则;③当 时,y<0,;④已知C(0,2),D(0,4),当取最小值时,.其中正确结论的序号是.20. 已知抛物线( , , 是常数)开口向下,过 , 两点,且.下列四个结论:
19. 关于抛物线 , 与x轴交于A、B两点(A在B左侧),给出下列4个结论:①当抛物线的顶点在y轴的正半轴上时,;②点P在抛物线上,当符合条件(a为常数)的点有3个时,则;③当 时,y<0,;④已知C(0,2),D(0,4),当取最小值时,.其中正确结论的序号是.20. 已知抛物线( , , 是常数)开口向下,过 , 两点,且.下列四个结论:①;
②若 , 则;
③若点 , 在抛物线上, , 且 , 则;
④当时,关于的一元二次方程必有两个不相等的实数根.
其中正确的是(填写序号).
三、综合题
-
21. 平面直角坐标系中,已知抛物线经过 , 两点,其中为常数.(1)、求的值,并用含的代数式表示;(2)、若抛物线与轴有公共点,求的值;(3)、设 , 是抛物线上的两点,请比较与0的大小,并说明理由.22. 已知二次函数y=ax2-2ax+c(a>0)的图象与x轴的交点坐标为(2,0).(1)、求抛物线的对称轴及c的值.(2)、若该抛物线与直线y=x-2只有一个公共点.
①求a的值;
②若点A(x1 , y1),B(x2 , y2)在该抛物线上,当m-1≤x1≤m+1,m+1≤x2≤m+2时,均满足y1≠y2 , 求m的取值范围.
23. 在直角坐标系中,点A(1,m)和点B(3,n)在二次函数y=ax2+bx+1(a#0)的图象上.(1)、若m=1,n=4,求二次函数的表达式及图象的对称轴.(2)、若m-n= ,试说明二次函数的图象与x轴必有交点.(3)、若点C(x0 , y0)是二次函数图象上的任意一点,且满足y0≤m,求mn的取值范围.24. 在平面直角坐标系内,设二次函数y1=(x-a)2+a-1(a为常数).(1)、若函数y1的图象经过点(1,2),求函数y1的表达式.(2)、若函数y1的图象与一次函数y2=x+b(b为常数)的图象有且仅有一个交点,求b的值.(3)、已知(m,n)( m>0)在函数y1的图象上,当m>2a时,求证:n>.