人教版九年级上对接中考知识点复习专项计划——一元二次方程的应用

试卷更新日期：2022-09-26 类型：复习试卷

进入出卷网下载

一、单选题

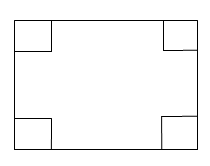
1. 如图，在长为10cm，宽为8cm的矩形的四个角上截去四个全等的正方形，使得留下的图形面积是原矩形面积的80%，所截去的小正方形的边长是多少？设小正方形的边长是xcm，下列方程正确的是（）

A、 $(10 - x) (8 - x) = 10 \times 8 \times 80 %$ B、 $(10 - 2 x) (8 - 2 x) = 10 \times 8 \times 80 %$ C、 $(10 - x) (8 - x) = 10 \times 8 \times 20 %$ D、 $10 \times 8 - 4 x^{2} = 10 \times 8 \times 80 %$

查看试题解析
2. 今年为庆祝共青团成立100周年，教体局举行篮球友谊赛，初赛采用单循环制（每两支球队之间都进行一场比赛），据统计，比赛共进行了28场，则一共邀请了多少支球队参加比赛？设一共邀请了x支球队参加比赛．根据题意可列方程是（）

A、 $\frac{x (x + 1)}{2} = 28$ B、 $x (x - 1) = 28$ C、 $\frac{x (x - 1)}{2} = 28$ D、 $x (x - 3) = 28$

查看试题解析
3. 电影《长津湖》讲述了一段波澜壮阔的历史，自上映以来，全国票房连创佳绩．据不完全统计，某市第一天票房收入约 $2$ 亿元，第三天票房收入约达到 $4$ 亿元，设票房收入每天平均增长率为 $x$ ，下面所列方程正确的是（）

A、 $2 (1 + x)^{2} = 4$ B、 $2 (1 + 2 x) = 4$ C、 $2 (1 - x)^{2} = 4$ D、 $2 + 2 (1 + x) + 2 (1 + x)^{2} = 4$

查看试题解析
4. 国家统计局统计数据显示，我国快递业务逐年增加，2019年至2021年我国快递业务收入由7500亿元增加到9000亿元．设我国2019年至2021年快递业务收入的年平均增长率为 $x$ ，则可列方程为（）

A、 $7500 (1 + 2 x) = 9000$ B、 $7500 \times 2 (1 + x) = 9000$ C、 $7500 {(1 + x)}^{2} = 9000$ D、 $7500 + 7500 (1 + x) + 7500 {(1 + x)}^{2} = 9000$

查看试题解析
5. 新冠疫情牵动人心，若有一人感染了新冠，在每轮传染中平均一个人可以传染 $x$ 个人，经过两轮传染后共有400人感染，列出的方程是（）

A、 $1 + x + x^{2} = 400$ B、 ${(1 + x)}^{2} = 400$ C、 $x + x (1 + x) = 400$ D、 $1 + 2 x = 400$

查看试题解析
6. 2020年北京冬奥会吉祥物“冰墩墩”敦厚可爱，深受大家欢迎.某生产厂家1月份平均日产量为20000个，随着冬奥会的举行，“冰墩墩”一路走红，供不应求.为满足市场需求，工厂决定扩大产能，3月份平均日产量达到33800个，设1至3月份冰墩墩日产量的月平均增长率为 $x$ ，则可列方程为（）

A、 $20000 (1 + x) = 33800$ B、 $20000 (1 + 2 x) = 33800$ C、 $20000 {(1 + x)}^{2} = 33800$ D、 $20000 (1 + x^{2}) = 33800$

查看试题解析
7. 某超市销售一批玩具，平均每天可售出120件，每件盈利4元，市场调查发现售价每涨1元，销售量减少10件；售价每降1元，销售量增加10件。爱动脑的嘉嘉发现：在一定范围内，涨a元与降b元所获得的利润相同，则a与b满足（）

A、a﹣b＝4 B、a﹣b＝8 C、a+b＝4 D、a+b＝8

查看试题解析
8. 某商店销售一批运动装，平均每天可销售20套，每套盈利45元；为扩大销售量，增加盈利，采取降价措施，毎降价1元，平均每天可多卖4套，若商店想要平均每天获利2100元，设每套运动装应降价x元，则可列方程为（）

A、(45-x)(20+4x)＝2100 B、(45+x)(20+4x)＝2100 C、(45-x)(20-4x)＝2100 D、(45+x)(20-4x)＝2100

查看试题解析
9. 某超市销售一种商品，其进价为每千克30元，按每千克45元出售，每天可售出300千克，为让利于民，超市采取降价措施，当售价每千克降低1元时，每天销量可增加50千克，若每天的利润要达到5500元，则实际售价应定为多少元？设售价每千克降低x元，可列方程为（）

A、（45-30-x）（300+50x）=5500 B、（x-30）（300+50x）=5500 C、（x-30）[300+50（x-45）]=5500 D、（45-x）（300+50x）=5500

查看试题解析
10. 在肥西悬主城区，共享单车为市民出行带来了方便，某单车公司第一个月投放1000辆单车，计划第三个月投放单车数量比第一个月多690辆．设该公司第二、三两个月投放单车数量的月平均增长率为x，则所列方程正确的为（）

A、 $1000 {(1 + x)}^{2} = 1000 + 690$ B、 $1000 {(1 + x)}^{2} = 690$ C、 $690 {(1 + x)}^{2} = 1000$ D、 $1000 (1 + 2 x) = 1000 + 690$

查看试题解析
11. 疫情期间居民为了减少外出时间，更愿意使用APP在线上购物，某购物APP今年二月份用户比一月份增加了44%，三月份用户比二月份增加了21%，求二、三两个月用户的平均每月增长率.设二、三两个月平均增长率为x，下列方程正确的是（）

A、 $2 {(1 + x)}^{2} = (1 + 44 %) (1 + 21 %)$ B、 ${(1 + 2 x)}^{2} = (1 + 44 %) (1 + 21 %)$ C、 ${(1 + x)}^{2} = (1 + 44 %) (1 + 21 %)$ D、 $1 + (1 + x) + {(1 + x)}^{2} = (1 + 44 %) (1 + 21 %)$

查看试题解析

二、填空题

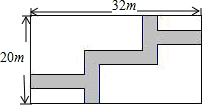
12. 随着新冠疫情趋于缓和，口罩市场趋于饱和，某N95口罩每盒原价为200元，连续两次降价后每盒的售价为72元，则平均每次下降的百分率为．

查看试题解析
13. 参加足球联赛的每两支球队之间都要进行两场比赛，共要比赛42场，则参加比赛的球队有支．

查看试题解析
14. 某种植物的主干长出若干数目的支干，每个支干又长出同样多数目的小分支，主干、支干、小分支一共是43个，则每个支干长出的小分支数目为．

查看试题解析
15. 如图，在宽为20m，长为32m的矩形地面上修筑同样宽的道路，余下的部分种上草坪，要使草坪的面积为540m² ，求道路的宽若设道路宽为xm，则根据题意可列方程为

查看试题解析

三、解答题

16. 目前，以5G为代表的战略性新兴产业蓬勃发展，某市2019年底有5G用户2万户，计划到2021年底5G用户数达到9.68万户，求这两年全市5G用户数的年平均增长率．

查看试题解析
17. 我市茶叶专卖店销售某品牌茶叶，其进价为每千克240元，按每千克400元出售，平均每周可售出200千克，后来经过市场调查发现，单价每降低10元，则平均每周的销售量可增加40千克．若该专卖店销售这种品牌茶叶要想平均每周获利41600元，在平均每周获利不变的情况下，为尽可能让利于顾客，赢得市场，每千克茶叶应降价多少元？

查看试题解析

四、综合题

18. 某大型电子商场销售某种空调，每台进货价为2500元，标价为3200元．

(1)、若电子商场连续两次降价，每次降价的百分率相同，最后以2592元售出，求每次降价的百分率；

(2)、市场调研表明：当每台售价为3000元时，平均每天能售出10台，当每台售价每降100元时，平均每天就能多售出4台，若商场要想使这种空调的销售利润平均每天达到5400元，且顾客得到优惠，则每台空调的定价应为多少元？

查看试题解析
19. 2022年北京冬奥会吉祥物冰墩墩开售时，就深受大家的喜欢．某供应商今年2月第一周购进冰墩墩200个，因销售量火爆，第三周购进冰墩墩288个，若购进冰墩墩数量的周平均增长率相同．

(1)、求今年2月第二周购进冰墩墩多少个？

(2)、今年2月第一周，一个冰墩墩的售价定为100元，本周有m个冰墩墩没有售完：从第二周开始，供应商决定调整冰墩墩的售价，每个冰墩墩的售价在第一周的基础上，下降m元；由于冬奥赛事的火热进行，到第二周结束购进的冰墩墩全部售完，若这两周的总销售额为41500元，求m的值．

查看试题解析
20. 2022年冬奥会吉祥物冰墩墩深受人们喜爱，冬奥会特许商店将进货价为每个30元的冰墩墩饰品以40元的价格售出，平均每月能售出600个，调查表明：这种冰墩墩饰品的售价每上涨1元，其销售量就减少10个，同时规定售价在40-60元范围内．

(1)、当售价上涨x元时，销售量为个；

(2)、为了实现销售这种饰品平均每月10000元的销售利润，每个饰品应定为多少元？这时售出冰墩墩饰品多少个？

查看试题解析
21. 2022年2月4日，万众瞩目的冬奥会在我们的首都北京开幕了，与往届冬奥会所不同的是，这届冬奥会大家都被吉祥物—冰墩墩吸引了，导致市场大量缺货，为满足市场需求，温州某玩具加工厂打算紧急招聘70名工人进行冰墩墩的制作，已知冰墩墩分为普通款和升级款两种款式，普通工人每人每天可以生产2件普通款或1件升级款，根据市场行情，普通款每件利润为140元，升级款每件利润为350元，为保证全部售出，每生产1件升级款就将升级款的售价降低5元（每件利润不低于150元），设每天生产升级款 $x$ 件．

(1)、根据信息填表：
产品种类
每天工人数（人）
每天的产量（件）
每件可获得的利润（元）
普通款冰墩墩
升级款冰墩墩
$x$
$x$

(2)、当 $x$ 取多少时，工厂每日的利润可达到17200元？

查看试题解析
22. 某购物商场销售一批名牌衬衫，平均每天可售出20件，每件盈利40元；为了扩大销售，增加盈利，尽快减少库存，商场决定采取适当的降价措施．经调查发现，每件衬衫每降价1元，商场平均每天可多售出2件．

(1)、每天销售这种衬衫的盈利要达到1200元，则每件衬衫应降价多少元？

(2)、每件衬衫降价多少元时，商场每天盈利最多？利润是多少？

查看试题解析
23. 如图，某中学课外兴题小组准备围建一个矩形花园 ABCD，其中一边靠墙，另外三边用总长为60 m的篱笆围成，与墙平行的一边 BC上要预留2 m宽的入口（如图中MN所示，不用篱笆），已知墙长为 28 m．

(1)、当矩形的长BC为多少米时，矩形花园的面积为300平方米；

(2)、能否围成500平方米的矩形花园?若能求出 BC长；若不能，说明理由．

查看试题解析
24. 如图，某校劳动小组计划利用已有的一堵长为6m的墙，用篱笆围成一个面积为12m²的矩形劳动基地ABCD，边AD的长不超过墙的长度，在BC边上开设宽为1m的门EF（门不需要篱笆）．设AB的长为x（m），BC的长为y（m）．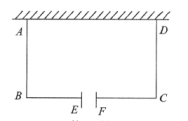

(1)、求y关于x的函数表达式．

(2)、若围成矩形劳动基地ABCD三边的篱笆总长为10m，求AB和BC的长度．

(3)、若AB和BC的长都是整数（单位：m），且围成矩形劳动基地ABCD三边的篱笆总长小于10m，请直接写出所有满足条件的围建方案．

查看试题解析
25. 2022年冬奥会在北京顺利召开，冬奥会吉祥物冰墩墩公仔爆红．据统计冰墩墩公仔在某电商平台1月份的销售量是5万件，3月份的销售量是7.2万件．

(1)、若该平台1月份到3月份的月平均增长率都相同，求月平均增长率是多少？

(2)、市场调查发现，某一间店铺冰墩墩公仔的进价为每件60元，若售价为每件100元，每天能销售20件，售价每降价1元，每天可多售出2件，为了推广宣传，商家决定降价促销，同时尽量减少库存，若使销售该公仔每天获利1200元，则售价应降低多少元？

查看试题解析
26. 工艺商场按标价销售某种工艺品时，每件可获利45元；按标价的八五折销售该工艺品8件与将标价降低35元销售该工艺品12件所获利润相等.

(1)、该工艺品每件的进价、标价分别是多少元？

(2)、若每件工艺品按（1）中求得的进价进货，标价售出，工艺商场每天可售出该工艺品100件.若每件工艺品降价1元，则每天可多售出该工艺品4件.问每件工艺品降价多少元出售，每天获得的利润可为4000元且成本较低？

查看试题解析
27. 某文具店销售A、B两款文具盒，其中A款文具盒的定价为15元/个，B款文具盒的定价为23元/个，A款文具盒的成本为7元/个，B款文具盒的成本为10元/个.

(1)、开业当月，该文具店按照定价售出A、B两款文具盒共180个，销售总额为3340元，则A款文具盒和B款文具盒分别销售了多少个？

(2)、根据开业当月试销售的情况，商家决定第二月将A款文具盒的售价在定价的基础上提高a元，第二月A款文具盒的销量比开业当月降低了2a个，同时商家推出买一个B款文具盒赠送一块成本为1元的橡皮擦的活动，第二月B款文具盒的销量比开业当月提高了a个，结果第二月销售A、B两款文具盒的总利润比开业当月获得的总利润多 $(76 a - 30)$ 元，求a的值.

查看试题解析

产品种类	每天工人数（人）	每天的产量（件）	每件可获得的利润（元）
普通款冰墩墩
升级款冰墩墩	$x$	$x$