人教版八上数学第十三章13.4最短路径 课时易错题三刷（第三刷）
试卷更新日期：2022-09-26 类型：同步测试
一、单选题
-
1. 如图，在 中， ＝ ＝6，且 ， ， 是 的两条高线，P是 上一动点，则 的最小值是（ ）
A、4 B、5 C、6 D、82. 如图所示，在四边形ABCD中， ，AC=1， ，直线MN为线段AD的垂直平分线，P为MN上的一个动点，则PC+PD的最小值为（ ）
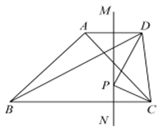A、1 B、 C、 D、33. 如图， ABC≌ AED，BC与ED交于点F，连接AF，P为线段AF上一动点，连接BP、DP，EF＝3，CF＝5，则BP+DP的最小值是（ ）
A、4 B、8 C、10 D、164. 如图，点C、D在线段AB的同侧，CA＝4，AB＝12，BD＝9，M是AB的中点，∠CMD＝120°，则CD长的最大值是（ ）
A、16 B、19 C、20 D、215. 如图，正 的边长为 ，过点 的直线 ，且 与 关于直线 对称， 为线段 上一动点，则 的最小值是（ ）
A、 B、 C、 D、二、填空题
-
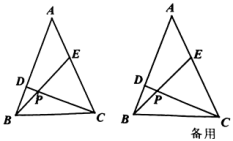
6. 已知△ABC的面积是12，AB=AC=5，AD是BC边上的中线，E，P分别是AC，AD上的动点，则CP+EP的最小值为 ．
7. 如图，在Rt△ABC中，∠ACB=90°，EF垂直平分AB，AC=3，BC=4，则AE+CE的最小值是.
8. 如图， 是等边三角形， ，点 、 分别为边 、 上的动点，当 的周长最小时， 的度数是.
9. 如图，在△ABC中，∠C＝90°，AC＝8cm ， BC＝6cm ， AB=10cm，点E在AC上，现将△BCE沿BE翻折，使点C落在点C′处连接AC′，则AC′长度的最小值是 ．
三、作图题
-
10. 画图题
(1)、在图1中找出点A ， 使它到M ， N两点的距离相等，并且到OH ， OF的距离相等．(2)、如图2，①写出△ABC关于x轴对称的△A1B1C1的各顶点的坐标；②画出△ABC关于y轴对称的△A2B2C2；
③在y轴上求作一点P ， 使△PBC的周长最小．
11. 如图，在所给的网格图中，完成下列各题（用直尺画图，否则不给分）
⑴画出格点△ABC关于直线DE的对称的△A1B1C1；
⑵在DE上画出点P，使PA+PC最小；
⑶在DE上画出点Q，使QA﹣QB最大．
四、综合题
-
12. 已知：如图，ABC中，AB＝AC，∠A＝45°，E是AC上的一点，∠ABE＝∠ABC，过点C作CD⊥AB于D，交BE于点P．
(1)、直接写出图中除ABC外的所有等腰三角形；(2)、求证：BD＝PC；(3)、点H、G分别为AC、BC边上的动点，当DHG周长取取小值时，求∠HDG的度数．13. 如图
(1)、①作出 关于y轴对称的 ．②通过画图在x轴上找出点P，使得 与 之和最小．
(2)、连接 、 、 ，则 的面积为 ．14. 如图，在等腰三角形 ABC 中，AB＝AC，AD⊥BC 于点 D，∠ABC 的角平分线 BE 交 AD 于点 F，且BF＝FA，BE＝AB，EG⊥BC 于点G.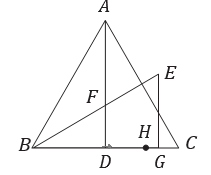
(1)、求证：∠BAD＝∠EBG；(2)、求证：AD＝DG＋EG；(3)、点H 为线段DG 上的一个动点，当AH＋HE 的值最小时，求∠DAH 的度数.15. 如图
(1)、性质：角平分线上的点到角两边的距离相等，如图1：OP平分∠MON，PC⊥OM于C，PB⊥ON于B，则PBPC（填“ ”“ ”或“=”）；(2)、探索：如图2，小明发现，在△ABC中，AD是∠BAC的平分线，则 ，请帮小明说明原因.(3)、应用：如图3，在小区三条交叉的道路AB，BC，CA上各建一个菜鸟驿站D，P，E，工作人员每天来回的路径为P→D→E→P，①问点P应选在BC的何处时，才能使PD+DE+PE最小？
②若∠BAC=30°，S△ABC=10，BC=5，则PD+DE+PE的最小值是多少？