人教版八上数学第十三章13.4最短路径 课时易错题三刷（第一刷）
试卷更新日期：2022-09-26 类型：同步测试
一、单选题
-
1. 点D、E分别是等边三角形 的边 、 的中点， ，F是AD上一动点，则 的最小值是（ ）
A、6 B、7 C、8 D、92. 如图，等腰三角形的底边长为4，面积是16，腰的垂直平分线分别交 ， 边于E，F点若点D为边的中点，点M为线段上动点，则周长的最小值为 ．
3. 如图，若∠AOB=44°，P为∠AOB内一定点，点M在OA上，点N在OB上，当△PMN的周长取最小值时，∠MPN的度数为（ ）
A、82° B、84° C、88° D、92°4. 如图所示，在四边形ABCD中， ， ， ， ， 在AD上找一点P，使的值最小；则的最小值为（ ）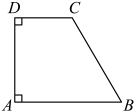
A、4 B、3 C、5 D、65. 如图，在四边形 中， ， ， 面积为21， 的垂直平分线 分别交 于点 ，若点P和点Q分别是线段 和 边上的动点，则 的最小值为（ ）
A、5 B、6 C、7 D、86. 如图，等边 中，D为AC中点，点P、Q分别为AB、AD上的点， ， ，在BD上有一动点E，则 的最小值为（ ）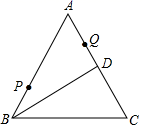
A、7 B、8 C、10 D、127. 如图，∠AOB=20°，点M、N分别是边OA、OB上的定点，点P、Q分别是边OB、OA上的动点，记∠MPQ= ，∠PQN= ，当MP+PQ+QN最小时，则 的值为（ ）
A、10° B、20° C、40° D、60°二、填空题
-
8. 如图，在△ABC中，∠ACB＝90°，∠A＝30°，边AC的垂直平分线DE分别交边AB、AC于点D、E、P为直线DE上一点．若BC＝2，则△BCP周长的最小值为 ．
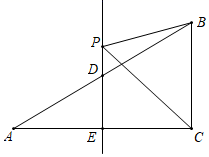9. 如图，在△ABC中，AB＝AC，BC＝5，△ABC的面积为20，DE垂直平分AC，分别交边AB，AC于点D，E，点F为直线DE上一动点，点G为BC的中点，连接FG，FC，则FC＋FG的最小值为 ．
10. 如图，在△ABC中，AB＝AC，点P是∠ACB的平分线CD上的一动点， ， △ABC的面积为 ， 则PA＋PE的最小值为.
11. 如图，AB⊥BC，AD⊥DC，∠BAD＝116°，在BC、CD上分别找一点M、N，当 AMN周长最小时，∠AMN+∠ANM的度数是.
12. 如图， ， 在 的同侧， ， ， ，点 为 的中点，连接 ， ， ，若 ，则 的最大值为.
三、作图题
-
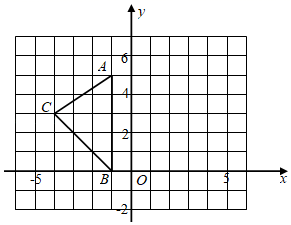
13. 如图，在平面直角坐标系中，A（-1，5），B（-1，0），C（-4，3）．
（ 1 ）作出△ABC关于y轴的对称图形△A'B'C'；
（ 2 ）写出点A'，B'，C'的坐标；
（ 3 ）在y轴上找一点P，使PA+PC的长最短．
四、综合题
-
14. 如图，四边形ABCD的对角线AC、BD相交于点E，若△ABC为等边三角形，AD⊥AB，AD＝DC＝4．
(1)、求证：BD垂直平分AC；(2)、求BE的长；(3)、若点F为BC的中点，请在BD上找出一点P，使PC+PF取得最小M值；PC+PF的最小值为（直接写出结果）．15. 已知点P在∠MON内．
(1)、如图1，点P关于射线OM的对称点是G，点P关于射线ON的对称点是H，连接OG、OH、OP．①若∠MON=50°，则∠GOH= ▲ ；
②若PO=5，连接GH，请说明当∠MON为多少度时，GH=10；
(2)、如图2，若∠MON=60°，A、B分别是射线OM、ON上的任意一点，当 PAB的周长最小时，求∠APB的度数．
-