人教版八上数学第十三章13.3.2等边三角形课时易错题三刷（第三刷）

试卷更新日期：2022-09-26 类型：同步测试

进入出卷网下载

一、单选题

1. 如图， $E$ 是等边 $Δ A B C$ 中 $A C$ 边上的点， $∠ 1 = ∠ 2$ ， $B E = C D$ ，则 $Δ A D E$ 是（）

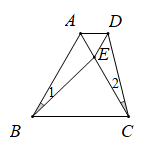A、等腰三角形 B、等边三角形 C、不等边三角形 D、无法确定

查看试题解析
2. 如图， $△ A B C$ 是等边三角形，D是线段 $A C$ 上一点（不与点A，C重合），连接 $B D$ ，点E，F分别在线段 $B A$ ， $B C$ 的延长线上，且 $D E = D F = B D$ ，则 $△ A E D$ 的周长等于（）

A、 $A B + A E$ B、 $B C + C F$ C、 $2 A C$ D、 $A C + B D$

查看试题解析
3. 如图，△ABC与△CED均为等边三角形，且B，C，D三点共线.线段BE，AD相交于点O，AF⊥BE于点F.若OF＝1，则AF的长为（）

A、1 B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、2

查看试题解析

二、填空题

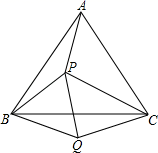
4. 如图，P是等边三角形ABC内的一点，且PA＝3，PB＝4，PC＝5，以BC为边在△ABC外作△BQC≌△BPA，连接PQ，则以下结论中正确的有（填序号）①△BPQ是等边三角形②△PCQ是直角三角形③∠APB＝150° ④∠APC＝120°

查看试题解析
5. 已知，如图，△ABC是等边三角形，AE=CD，BQ⊥AD于Q，BE交AD于点P，下列说法：①∠APE=∠C， ②AQ=BQ， ③BP=2PQ， ④AE+BD=AB，其中正确的是（填序号）.

查看试题解析
6. 如图，在等边△ABC中，AB=2，D为△ABC内一点，且DA=DB，E为△ABC外一点，BE=AB，且∠EBD =∠CBD，连接DE、CE，则下列结论； ①∠DAC=∠DBC；②BE⊥AC； ③∠DEB=30°.
④若EC//AD，则S_△_EBC₌1.其中正确的有．（只填序号）

查看试题解析
7. 如图，△ABC是边长为3的等边三角形，△BDC是等腰三角形，且∠BDC＝120°.以D为顶点作一个60°角，使其两边分别交AB于点M，交AC于点N，连接MN，则△AMN的周长为.

查看试题解析
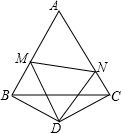8. 如图，D为等边三角形ABC内一点，AD=BD，BP=AB，∠DBP=∠DBC，则∠BPD=度．

查看试题解析

三、综合题

9. 如图，在等边 $△ A B C$ 中，点D是边 $A B$ 上一点，E是 $B C$ 延长线上一点， $C E = D A$ ，连接 $D E$ 交 $A C$ 于点F，过点D作 $D G ⊥ A C$ 于点G，过点D作 $D H ∥ B C$ 交 $A C$ 于点H．

(1)、求证： $A G = \frac{1}{2} A D$ ；

(2)、求证： $D F = E F$ ；

(3)、若 $C F = C E ， S_{△ A D G} = 2$ ，求出 $△ D G F$ 的面积．

查看试题解析
10. 如图

(1)、如图①，已知：在△ABC中，∠BAC＝90°，AB＝AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D，E．则线段DE、BD与CE之间的数量关系是；

(2)、如图②，将（1）中的条件改为：在△ABC中，AB＝AC，D，A，E三点都在直线m上，并且有∠BDA＝∠AEC＝∠BAC＝a，其中a为任意锐角或钝角．请问：（1）中的结论是还否成立？如成立，请你给出证明：若不成立，请说明理由；

(3)、拓展与应用：如图③，D，E是D，A，E三点所在直线m上的两动点（D，A，E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD，CE．若∠BDA＝∠AEC＝∠BAC，试判断△DEF的形状，并说明理由．

查看试题解析
11. 如图，在Rt△ABC中，∠B＝90°，AC＝10，∠C＝30°点D从点C出发沿CA方向以每秒2个单位长度的速度向点A匀速运动，同时点E从点A出发沿AB方向以每秒1个单位长度的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动.设点D、E运动的时间是t秒（t＞0），过点D作DF⊥BC于点F，连接DE、EF.

(1)、DF＝；（用含t的代数式表示）

(2)、求证：△AED≌△FDE；

(3)、当t为何值时，△DEF是等边三角形？说明理由；

(4)、当t为何值时，△DEF为直角三角形？（请直接写出t的值.）

查看试题解析
12. 在等边 $Δ A B C$ 中，线段 $A M$ 为 $B C$ 边上的中线.动点D在直线 $A M$ 上时，以 $C D$ 为一边在 $C D$ 的下方作等边 $Δ C D E$ ，连结BE.

(1)、若点D在线段 $A M$ 上时（如图），则 $A D$ $B E$ （填“＞”、“＜”或“=”）， $∠ C A M ＝$ 度；

(2)、设直线BE与直线 $A M$ 的交点为O.

①当动点D在线段 $A M$ 的延长线上时（如图），试判断 $A D$ 与 $B E$ 的数量关系，并说明理由；

②当动点D在直线 $A M$ 上时，试判断 $∠ A O B$ 是否为定值？若是，请直接写出 $∠ A O B$ 的度数；若不是，请说明理由.

查看试题解析
13. 已知，△ABC是等边三角形，BD是中线，延长BC至E，使CE＝CD．

(1)、如图1，求证：DB＝DE；

(2)、如图2，过点D作DE的垂线交BC于点F，连接AE，请直接写出图中所有面积等于△ABC面积一半的三角形．

查看试题解析
14. 如图，△ABC是边长为6的等边三角形，三边上分别有点E、D、F，使得AE＝BD＝CF，过点E作EP⊥DF，垂足为点P

(1)、求证：△BDE≌△CFD；

(2)、求∠DEP的度数；

(3)、当点E、D、F分别在三边BA、CB及AC的延长线上时，过点E作EP⊥DF，垂足为点P，若AE＝BD＝CF＝2，若△BDE的周长为19，求DP的长.

查看试题解析
15. 如图，点O是等边△ABC内一点，D是△ABC外的一点，∠AOB＝110°，∠BOC＝α，△BOC≌△ADC ， ∠OCD＝60°，连接OD ．

(1)、求证：△OCD是等边三角形；

(2)、当α＝150°时，试判断△AOD的形状，并说明理由；

(3)、当α＝时，△AOD是等腰三角形．

查看试题解析
16.

(1)、如图1所示，在 $△ A B C$ 中， $∠ A C B = 90 °$ ，BC的垂直平分线交AB于点D，垂足为E，当BD=5cm， $∠ B = 30 °$ ， $△ A C D$ 的周长=.

(2)、如图2所示，在 $△ A B C$ 中， $A B = A C$ ， $∠ A = 120 °$ ，D是BC的中点， $D E ⊥ A B$ ，垂足为E，那么 $B E ： E A =$ .

(3)、如图3所示，在等边△ABC中，D，E分别是BC，AC上的点，且AE=DC，AD，BE交于点P，作BQ⊥AD于点Q，若BP=2，求PQ的长.

查看试题解析
17. 已知，在等边△ABC中，点E在AB上，点D在CB的延长线上，且ED＝EC.

(1)、（特殊情况，探索结论）
如图1，当点E为AB的中点时，确定线段AE与DB的大小关系，请你直接写出结论：AEDB（选填“＞”，“＜”或“＝”）.

(2)、（特例启发，解答题目）
如图2，当点E为AB边上任意一点时，确定线段AE与DB的大小关系，请你直接写出，AEDB（选填“＞”，“＜”或“＝”）；理由如下：过点E作EF∥BC，交AC于点F.（请你完成以下解答过程）.

(3)、（拓展结论，设计新题）
在等边三角形ABC中，点E在直线AB上，点D在线段CB的延长线上，且ED＝EC，若△ABC的边长为1，AE＝2，则CD＝.

查看试题解析
18. 如图1，在△ABC中，AB＝AC，G为三角形外一点，且△GBC为等边三角形.

(1)、求证：直线AG垂直平分BC；

(2)、以AB为一边作等边△ABE（如图2），连接EG、EC，试判断△EGC是否构成直角三角形？请说明理由.

查看试题解析
19. 如图，AO是边长为2的等边△ABC的高，点D是AO上的一个动点（点D不与点A、O重合），以CD为一边在AC下方作等边△CDE，连接BE并延长，交AC的延长线于点F.

(1)、求证：△ACD≌△BCE；

(2)、当△CEF为等腰三角形时：
①求∠ACD的度数；

②求△CEF的面积.

查看试题解析
20. 如图，已知△ABC和△DCE均是等边三角形，点B、C、E在同一条直线上，AE与BD交于点O，AE与CD交于点G，AC与BD交于点F.

(1)、如图1，求证：∠1＝60°；

(2)、如图2，连结FG，求∠2的度数；

(3)、如图3，连结OC，若BD＝10，OC＝4，求△ACE的面积.

查看试题解析