人教版八上数学第十三章13.3.2等边三角形 课时易错题三刷（第二刷）
试卷更新日期：2022-09-26 类型：同步测试
一、单选题
-
1. 如图， 中， ， ， ，垂足为Q，延长MN至G，取 ，若 的周长为12， ，则 周长是（ ）
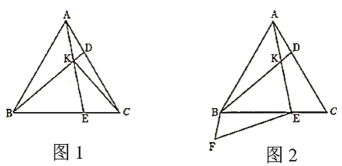
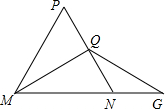A、8＋2m B、8＋m C、6＋2m D、6＋m2. 如图，△ABC是等边三角形，点E是AC的中点，过点E作EF⊥AB于点F，延长BC交EF的反向延长线于点D，若EF=1，则DF的长为（ ）
A、2 B、2.5 C、3 D、3.53. 如图， ， 点P在的内部，点C，D分别是点P关于、的对称点，连接交、分别于点E、F；若的周长的为10，则线段（ ）．
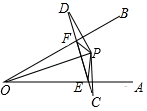A、8 B、9 C、10 D、114. 如图，在 中， ， ，D为 的中点，P为 上一点，E为 延长线上一点，且 有下列结论：① ；② 为等边三角形；③ ；④ 其中正确的结论是（ ）
A、①②③④ B、①② C、①②④ D、③④二、填空题
-
5. 如图，在△ABC中，∠ACB=90°，∠B =30°，CD是高．若AD=2，则BD= ．
6. 如图，是等边三角形，点E在AC的延长线上，点D在线段AB上，连接ED交线段BC于点F，过点F作于点N， ， ， 若 ， 则AN的长为 ．
三、解答题
-
7. 已知点P是线段MN上一动点，分别以PM，PN为一边，在MN的同侧作△APM，△BPN，并连接BM，AN．
（Ⅰ）如图1，当PM＝AP，PN＝BP且∠APM＝∠BPN＝90°时，试猜想BM，AN之间的数量关系与位置关系，并证明你的猜想；
（Ⅱ）如图2，当△APM，△BPN都是等边三角形时，（Ⅰ）中BM，AN之间的数量关系是否仍然成立？若成立，请证明你的结论；若不成立，试说明理由．
（Ⅲ）在（Ⅱ）的条件下，连接AB得到图3，当PN＝2PM时，求∠PAB度数．
四、综合题
-
8. 如图，点O是等边△ABC内一点，点D是△ABC外一点，∠AOB＝110°，∠BOC＝α，△BOC≌△ADC，连接OD．
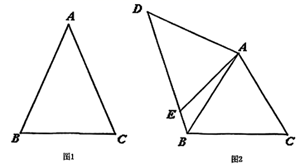
(1)、求证：△OCD是等边三角形；(2)、当α＝150°时，试判断△AOD的形状，并说明理由；(3)、当α＝∠AOB，AO＝8cm时，求OC的长度．9. 如图，△ABD，△AEC都是等边三角形，连接CD，BE交于点F．
求证：
(1)、∠BFC＝120°；(2)、FA平分∠DFE．10.
(1)、阅读理解：问题：如图1，在四边形 中，对角线 平分 ， .求证： .思考：“角平分线+对角互补”可以通过“截长、补短”等构造全等去解决问题.
方法1：在 上截取 ，连接 ，得到全等三角形，进而解决问题；
方法2：延长 到点N，使得 ，连接 ，得到全等三角形，进而解决问题.
结合图1，在方法1和方法2中任选一种 ， 添加辅助线并完成证明.
(2)、问题解决：如图2，在（1）的条件下，连接 ，当 时，探究线段 ， ， 之间的数量关系，并说明理由；(3)、问题拓展：如图3，在四边形 中， ， ，过点D作 ，垂足为点E，请直接写出线段 、 、 之间的数量关系.11. 如图， 和 中， ， 与 交于点P（不与点B，C重合），点B，E在 异侧， 、 的平分线相交于点I.
(1)、当 时，求 的长；(2)、求证： ；(3)、当 时， 的取值范围为 ，求m，n的值.12. 问题情境：七下教材第149页提出这样一个问题：如图1，∠AOB＝90°，OC平分∠AOB，把三角尺的直角顶点落在OC的任意一点P上，并使三角尺的两条直角边分别与OA、OB相交于点E、F，PE与PF相等吗？
(1)、七年级学习这部分内容时，我们还无法对这个问题的结论加以证明，八下教材第59页第11题不仅对这一问题给出了答案：“通过实验可以得到PE＝PF”，还要求“现在请你证明这个结论”，请你给出证明：(2)、变式拓展：
如图2，已知∠AOB＝120°，OC平分∠AOB，P是OC上一点，∠EPF＝60°，PE边与OA边相交于点E，PF边与射线OB的反向延长线相交于点F.试解决下列问题：①PE与PF还相等吗？为什么？
②试判断OE、OF、OP三条线段之间的数量关系，并说明理由.
13. 在边长为8的等边三角形 中，点Q是BC上一点，点P是AB上一动点，点P以1个单位每秒的速度从点A向点B移动，设运动时间为t秒.
(1)、如图1，若 ，当t取何值时 ？(2)、若点P从点A向点B运动，同时点Q以2个单位的速度从点B经点C向点A运动，当t为何值时， 为等边三角形（在图2中画出示意图）.(3)、如图3，将边长为 的等边三角形 变换为AB，AC为腰，BC为底的等腰三角形，且 ， ，点P运动到AB中点处静止后，点M，N分别为BC，AC上动点，点M以1个单位每秒的速度从点B向C运动，同时点N以a个单位每秒的速度从点C向A运动，当 ， 全等时，直接写出a的值.
-
