人教版八上数学第十三章13.3.2等边三角形 课时易错题三刷(第一刷)
试卷更新日期:2022-09-26 类型:同步测试
一、单选题
-
1. △BDE和△FGH是两个全等的等边三角形,将它们按如图的方式放置在等边三角形ABC内.若BC=5,则五边形DECHF的周长为( )
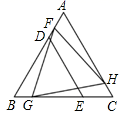 A、8 B、10 C、11 D、122. 如图,过边长为4的等边的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )
A、8 B、10 C、11 D、122. 如图,过边长为4的等边的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( ) A、 B、2 C、 D、3. 如图所示,已知在等边三角形ABC中,点D,E分别是BC,AC上的点,且AE=CD,连接AD,BE交于点P,过点B作BQ⊥AD,Q为垂足,PQ=2,则BP的长为( )
A、 B、2 C、 D、3. 如图所示,已知在等边三角形ABC中,点D,E分别是BC,AC上的点,且AE=CD,连接AD,BE交于点P,过点B作BQ⊥AD,Q为垂足,PQ=2,则BP的长为( ) A、3 B、4 C、5 D、64. 如图点在同一条直线上,都是等边三角形,相交于点O,且分别与交于点 , 连接 , 有如下结论:①;②;③为等边三角形;④.其中正确的结论个数是( )
A、3 B、4 C、5 D、64. 如图点在同一条直线上,都是等边三角形,相交于点O,且分别与交于点 , 连接 , 有如下结论:①;②;③为等边三角形;④.其中正确的结论个数是( )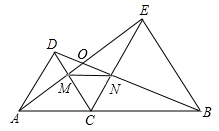 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
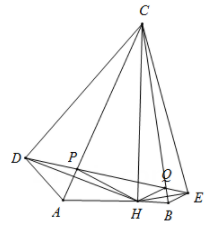
5. 如图,在 中, , ,高 .作点H关于 , 的对称点D,E,连接 交 于点P,交 于点Q;连接 , , , .下列结论:① ;② ;③五边形 的面积是24;④ 的周长为6.其中正确结论是.(填写序号)
三、解答题
-
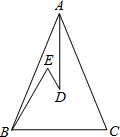
6. 如图,在△ABC中, , D、E是△ABC内的两点,AD平分∠BAC, . 若 , , 求BC的长.
 7. 如图,在△ABC中,AB=AC,D为AB边的中点,DE⊥AC于点E,DF⊥BC于点F,DE=DF.求证:△ABC是等边三角形.
7. 如图,在△ABC中,AB=AC,D为AB边的中点,DE⊥AC于点E,DF⊥BC于点F,DE=DF.求证:△ABC是等边三角形.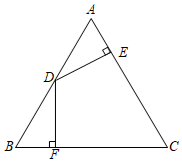
四、综合题
-
8. 如图,点D是等边△ABC内一点,E是△ABC外的一点,∠CDB=130°,∠BDA=α , △BDA≌△CEA .
 (1)、求证:△AED是等边三角形;(2)、若△CDE是直角三角形,求α的度数.9. 如图,在 中, ,AB边的垂直平分线分别交AB于点E,交AC于点F,点D在EF上,且 ,G是AC的中点,连接DG.
(1)、求证:△AED是等边三角形;(2)、若△CDE是直角三角形,求α的度数.9. 如图,在 中, ,AB边的垂直平分线分别交AB于点E,交AC于点F,点D在EF上,且 ,G是AC的中点,连接DG. (1)、求证: ;(2)、判断 是否是等边三角形,并说明理由.10. 如图,∠ACD是等边△ABC的一个外角,点E是∠ACD内部任意一点,作直线CE.
(1)、求证: ;(2)、判断 是否是等边三角形,并说明理由.10. 如图,∠ACD是等边△ABC的一个外角,点E是∠ACD内部任意一点,作直线CE. (1)、当CE平分∠ACD时,证明:AB∥CE.(2)、已知点A关于直线CE的对称点为F,连接AF、BF、CF,其中AF、BF分别交直线CE于P、Q两点.记∠ACE=α,当0<α<60°时,求∠BFC,(用含α的式子表示)(3)、若(2)中的α满足0°<α<120°时,
(1)、当CE平分∠ACD时,证明:AB∥CE.(2)、已知点A关于直线CE的对称点为F,连接AF、BF、CF,其中AF、BF分别交直线CE于P、Q两点.记∠ACE=α,当0<α<60°时,求∠BFC,(用含α的式子表示)(3)、若(2)中的α满足0°<α<120°时,①∠AFB= °;
②探究线段QB、QC、QP之间的数量关系,并证明.
11. 问题发现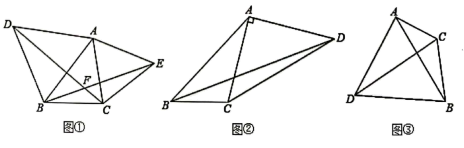 (1)、如图①,已知△ABC,以AB、AC为边向△ABC外分别作等边△ABD和等边△ACE,连接CD,BE.试猜想CD与BE的数量关系是;(2)、问题探究:如图②,四边形ABCD中,∠ABC=45°,∠CAD=90°,AC=AD,AB=2BC=6.求BD的长.(3)、问题解决:如图③,△ABC中,AC=2,BC=3,∠ACB是一个变化的角,以AB为边向△ABC外作等边△ABD,连接CD,求CD的长度最大值.12. 如图,是等边三角形, , 分别交AB,AC于点D,E.
(1)、如图①,已知△ABC,以AB、AC为边向△ABC外分别作等边△ABD和等边△ACE,连接CD,BE.试猜想CD与BE的数量关系是;(2)、问题探究:如图②,四边形ABCD中,∠ABC=45°,∠CAD=90°,AC=AD,AB=2BC=6.求BD的长.(3)、问题解决:如图③,△ABC中,AC=2,BC=3,∠ACB是一个变化的角,以AB为边向△ABC外作等边△ABD,连接CD,求CD的长度最大值.12. 如图,是等边三角形, , 分别交AB,AC于点D,E. (1)、求证:是等边三角形;(2)、点F在线段DE上,点G在外, , , 求证:.13. 如图所示,已知△ABC为等边三角形,AE=CD,AD、BE相交于点F.
(1)、求证:是等边三角形;(2)、点F在线段DE上,点G在外, , , 求证:.13. 如图所示,已知△ABC为等边三角形,AE=CD,AD、BE相交于点F. (1)、求证:△ABE≌△CAD;(2)、若BP⊥AD于点P,PF=6,求BF的长.
(1)、求证:△ABE≌△CAD;(2)、若BP⊥AD于点P,PF=6,求BF的长.
-


