人教版八上数学第十三章13.3.1等腰三角形 课时易错题三刷(第三刷)
试卷更新日期:2022-09-26 类型:同步测试
一、单选题
-
1. 如图,是等腰三角形, , , BP平分;点D是射线BP上一点,如果点D满足是等腰三角形,那么的度数是( ).
 A、20°或70° B、20°、70°或100° C、40°或100° D、40°、70°或100°2. 如图,△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论:①△BDF和△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长等于AB与AC的和;④BF=CF.其中正确的有( )
A、20°或70° B、20°、70°或100° C、40°或100° D、40°、70°或100°2. 如图,△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论:①△BDF和△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长等于AB与AC的和;④BF=CF.其中正确的有( ) A、①②③ B、①②③④ C、①② D、①3. 如图,∠BAD=90°,AC平分∠BAD,CB=CD,则∠B与∠ADC满足的数量关系为( )
A、①②③ B、①②③④ C、①② D、①3. 如图,∠BAD=90°,AC平分∠BAD,CB=CD,则∠B与∠ADC满足的数量关系为( ) A、∠B=∠ADC B、2∠B=∠ADC C、∠B+∠ADC=180° D、∠B+∠ADC=90°4. 等腰三角形一腰上的高与另一腰的夹角为20°,则其底角的大小为( )A、65° B、105° C、55°或35° D、65°或115°5. 如图, ,点B和点C是对应顶点, ,记 ,当 时, 与 之间的数量关系为( )
A、∠B=∠ADC B、2∠B=∠ADC C、∠B+∠ADC=180° D、∠B+∠ADC=90°4. 等腰三角形一腰上的高与另一腰的夹角为20°,则其底角的大小为( )A、65° B、105° C、55°或35° D、65°或115°5. 如图, ,点B和点C是对应顶点, ,记 ,当 时, 与 之间的数量关系为( ) A、 B、 C、 D、6. 如图,D为∠BAC的外角平分线上一点并且满足BD=CD,∠DBC=∠DCB,过D作DE⊥AC于E,DF⊥AB交BA的延长线于F,则下列结论:①△CDE≌△BDF;②CE=AB+AE;③∠BDC=∠BAC;④∠DAF=∠CBD.其中正确的结论有( )个
A、 B、 C、 D、6. 如图,D为∠BAC的外角平分线上一点并且满足BD=CD,∠DBC=∠DCB,过D作DE⊥AC于E,DF⊥AB交BA的延长线于F,则下列结论:①△CDE≌△BDF;②CE=AB+AE;③∠BDC=∠BAC;④∠DAF=∠CBD.其中正确的结论有( )个 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
7. 如图,在中,BD和CD分别是和的平分线,EF过点D,且 , 若 , , 则EF的长为 .
 8. 如图,△ABC中,AB=AC,作△BCE,点A在△BCE内,点D在BE上,AD垂直平分BE,且∠EBA+∠ECA=m°,则∠BAC=°.
8. 如图,△ABC中,AB=AC,作△BCE,点A在△BCE内,点D在BE上,AD垂直平分BE,且∠EBA+∠ECA=m°,则∠BAC=°. 9. 小聪在研究题目“如图,在等腰三角形ABC中, , , 的平分线与AB的垂直平分线OD交于点O,点C沿直线EF折叠后与点O重合,你能得出那些结论?”时,发现了下面三个结论:① ;②图中没有60°的角;③D、O、C三点共线.请你直接写出其中正确的结论序号:
9. 小聪在研究题目“如图,在等腰三角形ABC中, , , 的平分线与AB的垂直平分线OD交于点O,点C沿直线EF折叠后与点O重合,你能得出那些结论?”时,发现了下面三个结论:① ;②图中没有60°的角;③D、O、C三点共线.请你直接写出其中正确的结论序号:
三、综合题
-
10. 如图,在中, , 点D为边BC上一点,且 , 过点D作BC的垂线交AC于点E.
 (1)、求证:(2)、当时,求证:.11. 如图,在四边形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,CE⊥BD
(1)、求证:(2)、当时,求证:.11. 如图,在四边形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,CE⊥BD (1)、求证:△ABD≌△BCE;(2)、求证:AC是线段ED的垂直平分线.(3)、△DBC是等腰三角形吗?请说明理由.12. 如图,在ABC中,AC边的垂直平分线DM交AC于D,CB边的垂直平分线EN交BC于E,DM与EN相交于点F.
(1)、求证:△ABD≌△BCE;(2)、求证:AC是线段ED的垂直平分线.(3)、△DBC是等腰三角形吗?请说明理由.12. 如图,在ABC中,AC边的垂直平分线DM交AC于D,CB边的垂直平分线EN交BC于E,DM与EN相交于点F. (1)、若CMN的周长为16cm,求AB的长;(2)、若∠MFN=70°,求∠MCN的度数.13. 如图,在四边形 中, , 的平分线交 的延长线于点E,F是 的中点,连接 并延长交 于点G.
(1)、若CMN的周长为16cm,求AB的长;(2)、若∠MFN=70°,求∠MCN的度数.13. 如图,在四边形 中, , 的平分线交 的延长线于点E,F是 的中点,连接 并延长交 于点G.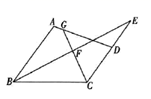 (1)、求证: 平分 .(2)、若 , ,求 的度数.14. 如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.设P点的运动时间为t.
(1)、求证: 平分 .(2)、若 , ,求 的度数.14. 如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.设P点的运动时间为t. (1)、CP=cm.(用含t的式子表示);(2)、若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;(3)、若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?15. 如图1所示,在 中, , 的垂直平分线交 于点 ,交 或 的延长线于点 .
(1)、CP=cm.(用含t的式子表示);(2)、若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;(3)、若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?15. 如图1所示,在 中, , 的垂直平分线交 于点 ,交 或 的延长线于点 . (1)、如图1所示,若 ,求 的大小;(2)、如图2所示,如果将(1)中的 的度数改为 ,其余条件不变,再求 的大小;(3)、你发现了什么规律?写出猜想,并说明理由.16. 如图,在△ABC中,AB=AC , 点D、E、F分别在AB、BC、AC边上,且BE=CF , BD=CE .
(1)、如图1所示,若 ,求 的大小;(2)、如图2所示,如果将(1)中的 的度数改为 ,其余条件不变,再求 的大小;(3)、你发现了什么规律?写出猜想,并说明理由.16. 如图,在△ABC中,AB=AC , 点D、E、F分别在AB、BC、AC边上,且BE=CF , BD=CE .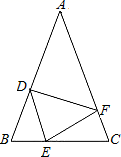 (1)、求证:△DEF是等腰三角形;(2)、当∠A=40°时,求∠DEF的度数.17. 如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD于E,交BA的延长线于F.
(1)、求证:△DEF是等腰三角形;(2)、当∠A=40°时,求∠DEF的度数.17. 如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD于E,交BA的延长线于F. (1)、求证:△ABD≌△ACF;(2)、若BD平分∠ABC,求证:CE= BD;(3)、若D为AC上一动点,∠AED如何变化,若变化,求它的变化范围;若不变,直接写出它的度数.18. 已知,在等腰 中, 于点D.以 为边作等边 ,直线 交直线 于点F,连接 .
(1)、求证:△ABD≌△ACF;(2)、若BD平分∠ABC,求证:CE= BD;(3)、若D为AC上一动点,∠AED如何变化,若变化,求它的变化范围;若不变,直接写出它的度数.18. 已知,在等腰 中, 于点D.以 为边作等边 ,直线 交直线 于点F,连接 .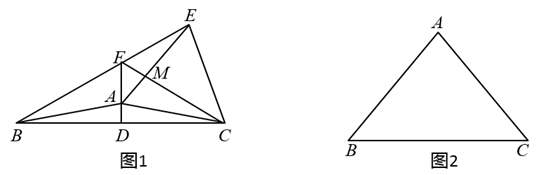 (1)、如图1, 与 在直线 的异侧,且 交 于点M.
(1)、如图1, 与 在直线 的异侧,且 交 于点M.①求证: ;
②猜想线段 之间的数量关系,并证明你的结论:
(2)、当 ,且 与 在直线 的同侧时,利用图2探究线段 之间的数量关系,并直接写出你的结论.19. 已知在△ABC中,点D在边BC上,点E在BC的延长线上,且BD=BA,CE=CA. (1)、如图①,若∠BAC=90°,∠B=45°,试求∠DAE的度数;(2)、若∠BAC=90°,∠B=60°,则∠DAE的度数为;(3)、如图②,若∠BAC>90°,其余条件不变,探究∠DAE与∠BAC之间有怎样的数量关系?并说明理由.20. 定义:顶角相等且顶点重合的两个等腰三角形叫做对顶三角形.如图1,在 OAB与 OCD中,OA=OB , OC=OD , ∠AOB=∠COD .
(1)、如图①,若∠BAC=90°,∠B=45°,试求∠DAE的度数;(2)、若∠BAC=90°,∠B=60°,则∠DAE的度数为;(3)、如图②,若∠BAC>90°,其余条件不变,探究∠DAE与∠BAC之间有怎样的数量关系?并说明理由.20. 定义:顶角相等且顶点重合的两个等腰三角形叫做对顶三角形.如图1,在 OAB与 OCD中,OA=OB , OC=OD , ∠AOB=∠COD .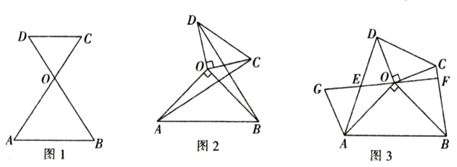 (1)、如图1, OAB与 OCD是对顶三角形,且A , O , C三点共线请判断AB与CD的位置关系,并说明理由.(2)、如图2, OAB与 OCD是对顶三角形,∠AOB=∠COD=90°,连接AC , BD , 试探究线段AC , BD之间的关系,并说明理由.(3)、如图3, OAB与 OCD是对顶三角形,∠AOB=∠COD=90°,连接AD , BC , 取AD的中点E , 连接EO并延长交BC于点F , 延长OE至点G , 使EG=OE , 连接AG , 求证:EF⊥BC .
(1)、如图1, OAB与 OCD是对顶三角形,且A , O , C三点共线请判断AB与CD的位置关系,并说明理由.(2)、如图2, OAB与 OCD是对顶三角形,∠AOB=∠COD=90°,连接AC , BD , 试探究线段AC , BD之间的关系,并说明理由.(3)、如图3, OAB与 OCD是对顶三角形,∠AOB=∠COD=90°,连接AD , BC , 取AD的中点E , 连接EO并延长交BC于点F , 延长OE至点G , 使EG=OE , 连接AG , 求证:EF⊥BC .