人教版八上数学第十三章13.3.1等腰三角形 课时易错题三刷（第一刷）
试卷更新日期：2022-09-26 类型：同步测试
一、单选题
-
1. 如图，已知平分 ， 于 ， ， 则下列结论：；；；；其中正确结论的个数有（ ）
A、1个 B、2个 C、3个 D、4个2. 若等腰三角形的一个外角是70°，则它的底角的度数是（ ）A、110° B、70° C、35° D、55°3. 如图， 中， ， ， 的垂直平分线分别交 于点E，F，与 ， 分别交于点D，G，则 的度数为（ ）
A、 B、 C、 D、4. 如图，△ABC中，AB＝AC，作△BCE，点A在△BCE内，点D在BE上，AD垂直平分BE，且∠BAC＝m°，则∠BEC＝（ ）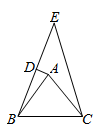
A、90°﹣ m° B、180°﹣2m° C、30°+ m° D、 m°5. 如图，在Rt△ABC中，∠ACB＝90°，∠CAB=36°，以C为原点，C所在直线为y轴，BC所在直线为x轴建立平面直角坐标系 ，在坐标轴上取一点M使△MAB 为等腰三角形，符合条件的 M 点有（ ）
A、6个 B、7个 C、8个 D、9个二、填空题
-
6. 如图， 、 的平分线相交于点F，过F作 ，交 于点D，交 于点E， ， ，则 .
7. 已知一个等腰三角形一腰与另一腰上高夹角为20°，则这个等腰三角形的顶角为 °．8. 如图，在中， ， ， 点在线段上运动（不与 ， 重合），连接 ， 作 ， 与交于.在点的运动过程中，的度数为时，的形状是等腰三角形.
三、解答题
-
9. 如图，和是顶角相等的等腰三角形，BC，DE分别是这两个等腰三角形的底边.求证.
四、综合题
-
10. 已知：如图 ABC中，AB=AC=10，BC=8，∠A=39°，AB的垂直平分线MN交AC于D，交AB于M，连接BD.
求：
(1)、∠DBC的度数；(2)、△BDC的周长.11. 如图①： 中， ，延长AC到E，过点E作 交AB的延长线于点F，延长CB到G，过点G作 交AB的延长线于H，且 .
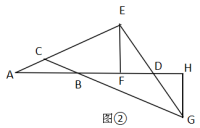(1)、求证： ≌ ；(2)、如图②，连接EG与FH相交于点D，若 ，求DH的长.12. 如图，在等腰△ABC与等腰△ADE中，AB=AC，AD=AE，∠BAC=∠DAE=α，连接BD和CE相交于点P，交AC于点M，交AD于点N．
(1)、求证：BD=CE．(2)、求证：AP平分∠BPE．(3)、若α=60°，试探寻线段PE、AP、PD之间的数量关系，并说明理由．13. 如图，在△ABC中， ， 点D、E、F分别在AB、BC、AC边上，且 ， ．
(1)、试说明：；(2)、当时，求∠DEF的度数；(3)、猜想：写出当∠A为多少度时， ．14. 如图
(1)、如图①，在△ABC中，D为△ABC外一点，若AC平分∠BAD，CE⊥AB于点E，∠B+∠ADC＝180°，求证：BC＝CD；琮琮同学：我的思路是在AB上取一点F，使得AD=AF，连结CF，先证明△ADC≌△AFC得到DC＝FC，再证明CB＝CF，从而得出结论；
宸宸同学：我觉得也可以过点C作边AD的高线CG，由角平分线的性质得出CG=CE，再证明△GDC≌△EBC，从而得出结论.请根据两位同学的思路选择一种写出证明过程.
(2)、如图②，D、E、F分别是等边△ABC的边BC、AB、 AC上的点， AD平分∠FDE， 且∠FDE=120°.求证：BE=CF.15. 在等腰△ABC中，AB=AC，点D是AC上一动点，点E在BD的延长线上，且AB=AE，AF平分∠CAE交DE于点F，连接FC．
(1)、如图1，求证：∠ABE=∠ACF；(2)、如图2，当∠ABC=60°时，在BE上取点M，使BM=EF，连接AM．求证：△AFM是等边三角形；(3)、如图3，当∠ABC=45°，且AEBC时，求证：BD=2EF．
-