安徽省江淮十校2022-2023学年高三上学期数学9月第一次联考试卷
试卷更新日期:2022-09-26 类型:月考试卷
一、单选题
-
1. 已知集合 , 则( )A、 B、 C、 D、2. 已知均为单位向量,且 , 则( )A、1 B、 C、2 D、33. 已知 , 则复数的虚部是( )A、-1 B、 C、1 D、4. 一家商店使用一架两臂不等长的天平称黄金.一位顾客到店里购买10克黄金,售货员先将5克的砝码放在天平左盘中,取出一些黄金放在天平右盘中使天平平衡;再将5克的砝码放在天平右盘中,再取出一些黄金放在天平左盘中使天平平衡;最后将两次称得的黄金交给顾客.顾客实际购买的黄金( )A、大于10克 B、小于10克 C、等于10克 D、不能判断大小5. 已知正项等比数列的前n项和为 , 前n项积为 , 满足 , 则的最小值是( )A、 B、 C、 D、6. 在正方体中,则下列判断错误的是( )
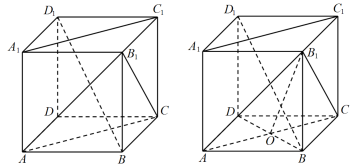 A、平面 B、平面∥平面 C、直线过的垂心 D、平面与平面夹角为7. 已知分别为椭圆的左右焦点,点P为椭圆上一点,以为圆心的圆与直线恰好相切于点P,则是( )A、 B、 C、 D、8. 已知函数是上的奇函数,且 , 且当时, , 则的值是( )A、2 B、 C、0 D、9. 已知在菱形中, , 把沿折起到位置,若二面角大小为 , 则四面体的外接球体积是( )
A、平面 B、平面∥平面 C、直线过的垂心 D、平面与平面夹角为7. 已知分别为椭圆的左右焦点,点P为椭圆上一点,以为圆心的圆与直线恰好相切于点P,则是( )A、 B、 C、 D、8. 已知函数是上的奇函数,且 , 且当时, , 则的值是( )A、2 B、 C、0 D、9. 已知在菱形中, , 把沿折起到位置,若二面角大小为 , 则四面体的外接球体积是( ) A、 B、 C、 D、10. 下列四个不等式中,成立的个数是( )
A、 B、 C、 D、10. 下列四个不等式中,成立的个数是( )①;②;③;④;
A、1 B、2 C、3 D、411. 已知函数 , 以下结论正确的是( )A、是的一个周期 B、函数在单调递减 C、函数的值域为 D、函数在内有6个零点12. 甲口袋中有3个红球,2个白球和5个黑球,乙口袋中有3个红球,3个白球和4个黑球,先从甲口袋中随机取出一球放入乙口袋,分别以和表示由甲口袋取出的球是红球,白球和黑球的事件;再从乙口袋中随机取出一球,以B表示由乙口袋取出的球是红球的事件,则下列结论中正确的是( )A、 B、事件与事件B相互独立 C、 D、二、填空题
-
13. 在的展开式中只有第5项二项式系数最大,则常数项为 .14. 安徽省地形具有平原、台地(岗地)、丘陵、山地等类型,其中丘陵地区占了很大比重,因此山地较多,著名的山也有很多.某校开设了研学旅行课程,该校有6个班级分别选择黄山、九华山、天柱山中的一座山作为研学旅行的地点,每座山至少有一个班级选择,则恰好有2个班级选择黄山的方案有种.15. 已知抛物线的焦点为F,过点F的直线交抛物线于A,B两点,延长交准线于点C,分别过点A,B作准线的垂线,垂足分别记为M,N,若 , 则的面积为 .16. 若不等式对一切恒成立,则的最大值为 .
三、解答题
-
17. 已知数列满足: .(1)、证明数列为等差数列,并求数列的通项公式.(2)、若 , 证明: .18. 在中,角A,B,C所对的边分别为a,b,c,其外接圆的半径为 , 且满足 .
 (1)、求角B.(2)、若边上的中线长为 , 求的面积和周长.19. 在三棱锥中,的面积为 , 点O为的中点, , 且 .
(1)、求角B.(2)、若边上的中线长为 , 求的面积和周长.19. 在三棱锥中,的面积为 , 点O为的中点, , 且 . (1)、求证:平面平面 .(2)、E为线段上的点,若与面所成的角为 , 求的长度.20. 华容道是古老的中国民间益智游戏,以其变化多端、百玩不厌的特点与魔方、独立钻石一起被国外智力专家并称为“智力游戏界的三个不可思议”.据《资治通鉴》注释中说“从此道可至华容也”.通过移动各个棋子,帮助曹操从初始位置移到棋盘最下方中部,从出口逃走.不允许跨越棋子,还要设法用最少的步数把曹操移到出口.2021年12月23日,在厦门莲坂外图书城四楼佳希魔方,厦门市新翔小学六年级学生胡宇帆现场挑战“最快时间解数字华容道”世界纪录,并以4.877秒打破了“最快时间解数字华容道”世界纪录,成为了该项目新的世界纪录保持者.
(1)、求证:平面平面 .(2)、E为线段上的点,若与面所成的角为 , 求的长度.20. 华容道是古老的中国民间益智游戏,以其变化多端、百玩不厌的特点与魔方、独立钻石一起被国外智力专家并称为“智力游戏界的三个不可思议”.据《资治通鉴》注释中说“从此道可至华容也”.通过移动各个棋子,帮助曹操从初始位置移到棋盘最下方中部,从出口逃走.不允许跨越棋子,还要设法用最少的步数把曹操移到出口.2021年12月23日,在厦门莲坂外图书城四楼佳希魔方,厦门市新翔小学六年级学生胡宇帆现场挑战“最快时间解数字华容道”世界纪录,并以4.877秒打破了“最快时间解数字华容道”世界纪录,成为了该项目新的世界纪录保持者.参考公式:对于一组数据 , 其回归直线的斜率和截距的最小
二乘估计公式分别为: ,
参考数据: ,
(1)、小明一周训练成绩如表所示,现用作为经验回归方程类型,求出该回归方程.第x(天)
1
2
3
4
5
6
7
用时y(秒)
105
84
49
39
35
23
15
(2)、小明和小华比赛破解华容道,首局比赛小明获得胜利的概率是0.6,在后面的比赛中,若小明前一局胜利,则他赢下后一局的概率是0.7,若小明前一局失利,则他赢下后一局比赛的概率为0.5,比赛实行“五局三胜”,求小明最终赢下比赛的概率是多少.