西藏2022年中考数学试卷
试卷更新日期:2022-09-23 类型:中考真卷
一、单选题
-
1. -2的倒数是( )A、2 B、 C、-2 D、2. 下列图形中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、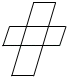 3. 我国神舟十三号载人飞船和航天员乘组于2022年4月16日返回地球,结束了183天的在轨飞行时间.从2003年神舟五号载人飞船上天以来,我国已有13位航天员出征太空,绕地球飞行共约2.32亿公里.将数据232000000用科学记数法表示为( )A、0.232×109 B、2.32×109 C、2.32×108 D、23.2×1084. 在一次中学生运动会上,参加男子跳高的8名运动员的成绩分别为(单位:m):1.75 1.80 1.75 1.70 1.70 1.65 1.75 1.60本组数据的众数是( )A、1.65 B、1.70 C、1.75 D、1.805. 下列计算正确的是( )A、2ab﹣ab=ab B、2ab+ab=2a2b2 C、4a3b2﹣2a=2a2b D、﹣2ab2﹣a2b=﹣3a2b26. 如图,l1∥l2 , ∠1=38°,∠2=46°,则∠3的度数为( )
3. 我国神舟十三号载人飞船和航天员乘组于2022年4月16日返回地球,结束了183天的在轨飞行时间.从2003年神舟五号载人飞船上天以来,我国已有13位航天员出征太空,绕地球飞行共约2.32亿公里.将数据232000000用科学记数法表示为( )A、0.232×109 B、2.32×109 C、2.32×108 D、23.2×1084. 在一次中学生运动会上,参加男子跳高的8名运动员的成绩分别为(单位:m):1.75 1.80 1.75 1.70 1.70 1.65 1.75 1.60本组数据的众数是( )A、1.65 B、1.70 C、1.75 D、1.805. 下列计算正确的是( )A、2ab﹣ab=ab B、2ab+ab=2a2b2 C、4a3b2﹣2a=2a2b D、﹣2ab2﹣a2b=﹣3a2b26. 如图,l1∥l2 , ∠1=38°,∠2=46°,则∠3的度数为( )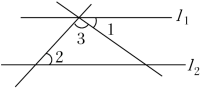 A、46° B、90° C、96° D、134°7. 已知关于x的一元二次方程(m﹣1)x2+2x﹣3=0有实数根,则m的取值范围是( )A、m≥ B、m< C、m>且m≠1 D、m≥且m≠18. 如图,数轴上A,B两点到原点的距离是三角形两边的长,则该三角形第三边长可能是( )
A、46° B、90° C、96° D、134°7. 已知关于x的一元二次方程(m﹣1)x2+2x﹣3=0有实数根,则m的取值范围是( )A、m≥ B、m< C、m>且m≠1 D、m≥且m≠18. 如图,数轴上A,B两点到原点的距离是三角形两边的长,则该三角形第三边长可能是( )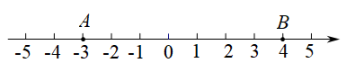 A、﹣5 B、4 C、7 D、89. 如图,AB是⊙O的弦,OC⊥AB,垂足为C, , OC=OD,则∠ABD的度数为( )
A、﹣5 B、4 C、7 D、89. 如图,AB是⊙O的弦,OC⊥AB,垂足为C, , OC=OD,则∠ABD的度数为( ) A、90° B、95° C、100° D、105°10. 在同一平面直角坐标系中,函数y=ax+b与(其中a,b是常数,ab≠0)的大致图象是( )A、
A、90° B、95° C、100° D、105°10. 在同一平面直角坐标系中,函数y=ax+b与(其中a,b是常数,ab≠0)的大致图象是( )A、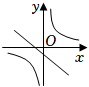 B、
B、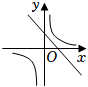 C、
C、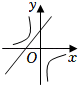 D、
D、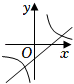 11. 如图,在菱形纸片ABCD中,E是BC边上一点,将△ABE沿直线AE翻折,使点B落在上,连接 . 已知∠C=120°,∠BAE=50°,则的度数为( )
11. 如图,在菱形纸片ABCD中,E是BC边上一点,将△ABE沿直线AE翻折,使点B落在上,连接 . 已知∠C=120°,∠BAE=50°,则的度数为( )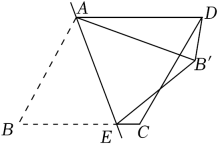 A、50° B、60° C、80° D、90°12. 按一定规律排列的一组数据: , , , , , , ….则按此规律排列的第10个数是( )A、 B、 C、 D、
A、50° B、60° C、80° D、90°12. 按一定规律排列的一组数据: , , , , , , ….则按此规律排列的第10个数是( )A、 B、 C、 D、二、填空题
-
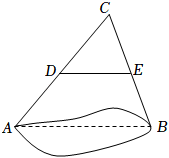
13. 比较大小:3.(选填“>”“<”“=”中的一个)14. 如图,如果要测量池塘两端A,B的距离,可以在池塘外取一点C,连接AC,BC,点D,E分别是AC,BC的中点,测得DE的长为25米,则AB的长为 米.
 15. 已知 , 都是实数,若 , 则 .16. 已知Rt△ABC的两直角边AC=8,BC=6,将Rt△ABC绕AC所在的直线旋转一周形成的立体图形的侧面积为 (结果保留π).17. 周末时,达瓦在体育公园骑自行车锻炼身体,他匀速骑行了一段时间后停车休息,之后继续以原来的速度骑行.路程s(单位:千米)与时间t(单位:分钟)的关系如图所示,则图中的a= .
15. 已知 , 都是实数,若 , 则 .16. 已知Rt△ABC的两直角边AC=8,BC=6,将Rt△ABC绕AC所在的直线旋转一周形成的立体图形的侧面积为 (结果保留π).17. 周末时,达瓦在体育公园骑自行车锻炼身体,他匀速骑行了一段时间后停车休息,之后继续以原来的速度骑行.路程s(单位:千米)与时间t(单位:分钟)的关系如图所示,则图中的a= .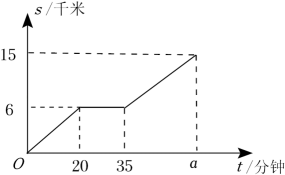 18. 如图,依下列步骤尺规作图,并保留作图痕迹:
18. 如图,依下列步骤尺规作图,并保留作图痕迹: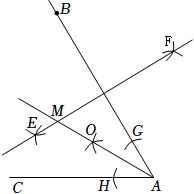
(1)分别以点A,B为圆心,大于AB的长为半径作弧,两弧相交于E,F两点,作直线EF;
(2)以点A为圆心,适当长为半径画弧,分别交AB,AC于点G,H,再分别以点G,H为圆心,大于GH的长为半径画弧,两弧在∠BAC的内部相交于点O,画射线AO,交直线EF于点M.
已知线段AB=6,∠BAC=60°,则点M到射线AC的距离为.三、解答题
-
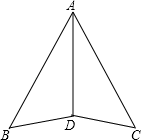
19. 计算: .20. 计算: .21. 如图,已知AD平分∠BAC,AB=AC.求证:△ABD≌△ACD.
 22. 教育部在《大中小学劳动教育指导纲要(试行)》中明确要求:初中生每周课外生活和家庭生活中,劳动时间不少于3小时.某走读制初级中学为了解学生劳动时间的情况,对学生进行了随机抽样调查,并将调查结果制成不完整的统计图表,如图:
22. 教育部在《大中小学劳动教育指导纲要(试行)》中明确要求:初中生每周课外生活和家庭生活中,劳动时间不少于3小时.某走读制初级中学为了解学生劳动时间的情况,对学生进行了随机抽样调查,并将调查结果制成不完整的统计图表,如图:平均每周劳动时间的频数统计表
劳动时间小时
频数
t<3
9
3≤t<4
a
4≤t<5
66
t≥5
15

请根据图表信息,回答下列问题.
(1)、参加此次调查的总人数是人,频数统计表中a=;(2)、在扇形统计图中,D组所在扇形的圆心角度数是°;(3)、该校准备开展以“劳动美”为主题的教育活动,要从报名的2男2女中随机挑选2人在活动中分享劳动心得,请用树状图或列表法求恰好抽到一名男生和一名女生的概率.23. 某班在庆祝中国共产主义青年团成立100周年活动中,给学生发放笔记本和钢笔作为纪念品.已知每本笔记本比每支钢笔多2元,用240元购买的笔记本数量与用200元购买的钢笔数量相同.(1)、笔记本和钢笔的单价各多少元?(2)、若给全班50名学生每人发放一本笔记本或一支钢笔作为本次活动的纪念品,要使购买纪念品的总费用不超过540元,最多可以购买多少本笔记本?24. 如图,在矩形ABCD中,AB=BC,点F在BC边的延长线上,点P是线段BC上一点(与点B,C不重合),连接AP并延长,过点C作CG⊥AP,垂足为E. (1)、若CG为∠DCF的平分线.请判断BP与CP的数量关系,并证明;(2)、若AB=3,△ABP≌△CEP,求BP的长.25. 某班同学在一次综合实践课上,测量校园内一棵树的高度.如图,测量仪在A处测得树顶D的仰角为45°,C处测得树顶D的仰角为37°(点A,B,C在一条水平直线上),已知测量仪高度AE=CF=1.6米,AC=28米,求树BD的高度(结果保留小数点后一位.参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).
(1)、若CG为∠DCF的平分线.请判断BP与CP的数量关系,并证明;(2)、若AB=3,△ABP≌△CEP,求BP的长.25. 某班同学在一次综合实践课上,测量校园内一棵树的高度.如图,测量仪在A处测得树顶D的仰角为45°,C处测得树顶D的仰角为37°(点A,B,C在一条水平直线上),已知测量仪高度AE=CF=1.6米,AC=28米,求树BD的高度(结果保留小数点后一位.参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75). 26. 如图,已知BC为⊙O的直径,点D为的中点,过点D作DG∥CE,交BC的延长线于点A,连接BD,交CE于点F.
26. 如图,已知BC为⊙O的直径,点D为的中点,过点D作DG∥CE,交BC的延长线于点A,连接BD,交CE于点F.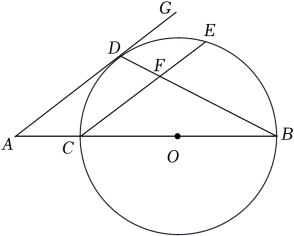 (1)、求证:AD是⊙O的切线;(2)、若EF=3,CF=5,tan∠GDB=2,求AC的长.27. 在平面直角坐标系中,抛物线y=﹣ +(m﹣1)x+2m与x轴交于A,B(4,0)两点,与y轴交于点C,点P是抛物线在第一象限内的一个动点.
(1)、求证:AD是⊙O的切线;(2)、若EF=3,CF=5,tan∠GDB=2,求AC的长.27. 在平面直角坐标系中,抛物线y=﹣ +(m﹣1)x+2m与x轴交于A,B(4,0)两点,与y轴交于点C,点P是抛物线在第一象限内的一个动点.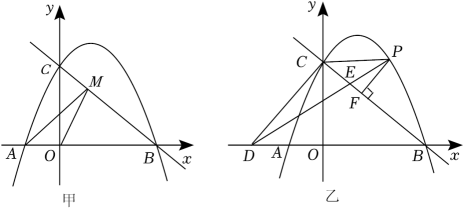 (1)、求抛物线的解析式,并直接写出点A,C的坐标;(2)、如图甲,点M是直线BC上的一个动点,连接AM,OM,是否存在点M使AM+OM最小,若存在,请求出点M的坐标,若不存在,请说明理由;(3)、如图乙,过点P作PF⊥BC,垂足为F,过点C作CD⊥BC,交x轴于点D,连接DP交BC于点E,连接CP.设△PEF的面积为S1 , △PEC的面积为S2 , 是否存在点P,使得最大,若存在,请求出点P的坐标,若不存在,请说明理由.
(1)、求抛物线的解析式,并直接写出点A,C的坐标;(2)、如图甲,点M是直线BC上的一个动点,连接AM,OM,是否存在点M使AM+OM最小,若存在,请求出点M的坐标,若不存在,请说明理由;(3)、如图乙,过点P作PF⊥BC,垂足为F,过点C作CD⊥BC,交x轴于点D,连接DP交BC于点E,连接CP.设△PEF的面积为S1 , △PEC的面积为S2 , 是否存在点P,使得最大,若存在,请求出点P的坐标,若不存在,请说明理由.