四川省巴中市2022年中考数学试卷
试卷更新日期:2022-09-23 类型:中考真卷
一、单选题
-
1. 下列各数是负数的是( )A、 B、 C、 D、2. 七巧板是我国的一种传统智力玩具,下列用七巧板拼成的图形是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
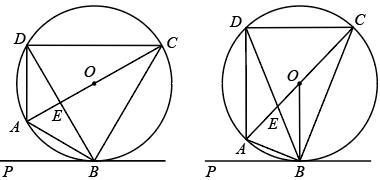
D、 3. 下列运算正确的是( )A、 B、 C、 D、4. 若一组数据1,2,4,3, , 0的平均数是2,则众数是( )A、1 B、2 C、3 D、45. 下列说法正确的是( )A、是无理数 B、明天巴中城区下雨是必然事件 C、正五边形的每个内角是 D、相似三角形的面积比等于相似比6. 如图,在平面直角坐标系中,为的边上一点, , 过作交于点 , 、两点纵坐标分别为1、3,则点的纵坐标为( )
3. 下列运算正确的是( )A、 B、 C、 D、4. 若一组数据1,2,4,3, , 0的平均数是2,则众数是( )A、1 B、2 C、3 D、45. 下列说法正确的是( )A、是无理数 B、明天巴中城区下雨是必然事件 C、正五边形的每个内角是 D、相似三角形的面积比等于相似比6. 如图,在平面直角坐标系中,为的边上一点, , 过作交于点 , 、两点纵坐标分别为1、3,则点的纵坐标为( )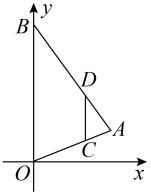 A、4 B、5 C、6 D、77. 对于实数 , 定义新运算: , 若关于的方程有两个不相等的实数根,则的取值范围( )A、 B、 C、且 D、且8. 如图,为的直径,弦交于点 , , , , 则( )
A、4 B、5 C、6 D、77. 对于实数 , 定义新运算: , 若关于的方程有两个不相等的实数根,则的取值范围( )A、 B、 C、且 D、且8. 如图,为的直径,弦交于点 , , , , 则( )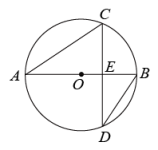 A、 B、 C、1 D、29. 在平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 将绕点逆时针旋转到如图的位置,的对应点恰好落在直线上,连接 , 则的长度为( )
A、 B、 C、1 D、29. 在平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 将绕点逆时针旋转到如图的位置,的对应点恰好落在直线上,连接 , 则的长度为( )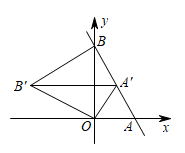 A、 B、 C、2 D、10. 如图,在菱形中,分别以、为圆心,大于为半径画弧,两弧分别交于点、 , 连接 , 若直线恰好过点与边交于点 , 连接 , 则下列结论错误的是( )
A、 B、 C、2 D、10. 如图,在菱形中,分别以、为圆心,大于为半径画弧,两弧分别交于点、 , 连接 , 若直线恰好过点与边交于点 , 连接 , 则下列结论错误的是( ) A、 B、若 , 则 C、 D、11. 甲、乙两人沿同一直道从地到地,在整个行程中,甲、乙离地的距离与时间之间的函数关系如图所示,下列说法错误的是( )
A、 B、若 , 则 C、 D、11. 甲、乙两人沿同一直道从地到地,在整个行程中,甲、乙离地的距离与时间之间的函数关系如图所示,下列说法错误的是( ) A、甲比乙早1分钟出发 B、乙的速度是甲的速度的2倍 C、若甲比乙晚5分钟到达,则甲用时10分钟 D、若甲出发时的速度为原来的2倍,则甲比乙提前1分钟到达地12. 函数的图象是由函数的图象轴上方部分不变,下方部分沿轴向上翻折而成,如图所示,则下列结论正确的是( )
A、甲比乙早1分钟出发 B、乙的速度是甲的速度的2倍 C、若甲比乙晚5分钟到达,则甲用时10分钟 D、若甲出发时的速度为原来的2倍,则甲比乙提前1分钟到达地12. 函数的图象是由函数的图象轴上方部分不变,下方部分沿轴向上翻折而成,如图所示,则下列结论正确的是( )① ;②;③;④将图象向上平移1个单位后与直线有3个交点.
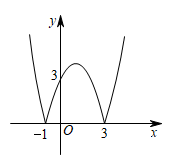 A、①② B、①③ C、②③④ D、①③④
A、①② B、①③ C、②③④ D、①③④二、填空题
-
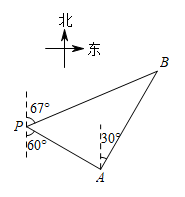
13. 今年是中国共青团建团100周年,据统计截止2021年12月31日,全国共有学生团员48310000名,48310000用科学记数法表示为 .14. 函数y= 中自变量x的取值范围是 .15. 因式分解: .16. 一艘轮船位于灯塔的南偏东方向,距离灯塔30海里的处,它沿北偏东方向航行一段时间后,到达位于灯塔的北偏东方向上的处,此时与灯塔的距离约为海里.(参考数据: , , )
 17. 、是关于的方程的两个实数根,且 , 则的值为 .18. 将双曲线向右平移2个单位,再向下平移1个单位,得到的新双曲线与直线相交于2022个点,则这2022个点的横坐标之和为 .
17. 、是关于的方程的两个实数根,且 , 则的值为 .18. 将双曲线向右平移2个单位,再向下平移1个单位,得到的新双曲线与直线相交于2022个点,则这2022个点的横坐标之和为 .三、解答题
-
19. 解答题(1)、计算: .(2)、先化简,再求值 , 其中 .(3)、求不等式组的整数解.20. 为扎实推进“五育并举”工作,某校利用课外活动时间开设了舞蹈、篮球、围棋和足球四个社团活动,每个学生只选择一项活动参加.为了解活动开展情况,学校随机抽取部分学生进行调查,将调查结果绘成如下表格和扇形统计图.
参加四个社团活动人数统计表
社团活动
舞蹈
篮球
围棋
足球
人数
50
30
80
参加四个社团活动人数扇形统计图

请根据以上信息,回答下列问题:
(1)、抽取的学生共有人,其中参加围棋社的有人;(2)、若该校有3200人,估计全校参加篮球社的学生有多少人?(3)、某班有3男2女共5名学生参加足球社,现从中随机抽取2名学生参加学校足球队,请用树状图或列表法说明恰好抽到一男一女的概率.21. 如图,▱ABCD中,E为BC边的中点,连接AE并延长交DC的延长线于点F,延长EC至点G,使CG=CE,连接DG、DE、FG.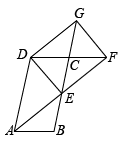 (1)、求证:△ABE≌△FCE;(2)、若AD=2AB,求证:四边形DEFG是矩形.22. 端午节吃粽子是中华民族的传统习俗,市场上猪肉粽进价比豆沙粽进价每盒贵10元,一盒猪肉粽加两盒豆沙粽进价为100元.(1)、求每盒猪肉粽和豆沙粽的进价;(2)、在销售中,某商家发现当每盒猪肉粽售价为50元时,每天可售出100盒,若每盒售价提高1元,则每天少售出2盒.设每盒猪肉粽售价为元,销售猪肉粽的利润为元,求该商家每天销售猪肉粽获得的最大利润.23. 如图,在平面直角坐标系中,直线与轴、轴分别交于点、两点,与双曲线交于点、两点, .
(1)、求证:△ABE≌△FCE;(2)、若AD=2AB,求证:四边形DEFG是矩形.22. 端午节吃粽子是中华民族的传统习俗,市场上猪肉粽进价比豆沙粽进价每盒贵10元,一盒猪肉粽加两盒豆沙粽进价为100元.(1)、求每盒猪肉粽和豆沙粽的进价;(2)、在销售中,某商家发现当每盒猪肉粽售价为50元时,每天可售出100盒,若每盒售价提高1元,则每天少售出2盒.设每盒猪肉粽售价为元,销售猪肉粽的利润为元,求该商家每天销售猪肉粽获得的最大利润.23. 如图,在平面直角坐标系中,直线与轴、轴分别交于点、两点,与双曲线交于点、两点, .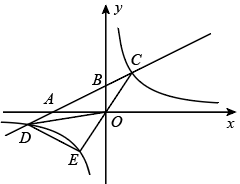 (1)、求 , 的值;(2)、求点坐标并直接写出不等式的解集;(3)、连接并延长交双曲线于点 , 连接、 , 求的面积.
(1)、求 , 的值;(2)、求点坐标并直接写出不等式的解集;(3)、连接并延长交双曲线于点 , 连接、 , 求的面积.