江苏省徐州市2022年中考数学试卷
试卷更新日期:2022-09-23 类型:中考真卷
一、单选题
-
1. ﹣3的绝对值是( )A、﹣3 B、3 C、- D、2. 下列图案是轴对称图形但不是中心对称图形的是( )A、
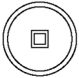 B、
B、 C、
C、 D、
D、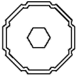 3. 要使得式子 有意义,则x的取值范围是( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 如图,已知骰子相对两面的点数之和为7,下列图形为该骰子表面展开图的是( )
3. 要使得式子 有意义,则x的取值范围是( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 如图,已知骰子相对两面的点数之和为7,下列图形为该骰子表面展开图的是( ) A、
A、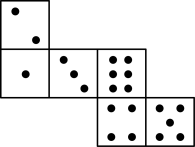 B、
B、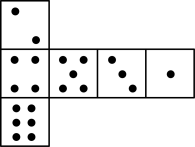 C、
C、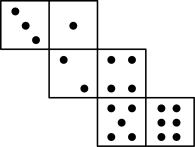 D、
D、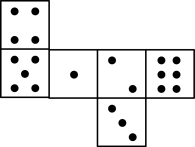 6. 我国近十年的人口出生率及人口死亡率如图所示.
6. 我国近十年的人口出生率及人口死亡率如图所示.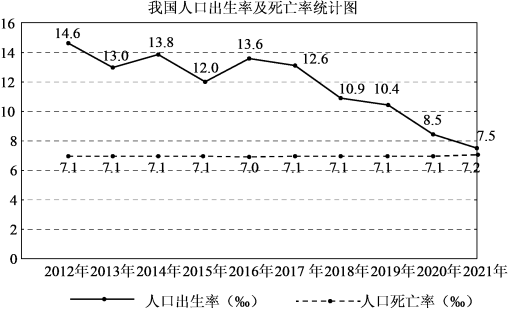
已知人口自然增长率=人口出生率—人口死亡率,下列判断错误的是( )
A、与2012年相比,2021年的人口出生率下降了近一半 B、近十年的人口死亡率基本稳定 C、近五年的人口总数持续下降 D、近五年的人口自然增长率持续下降7. 将一枚飞镖任意投掷到如图所示的正六边形镖盘上,若飞镖落在镖盘上各点的机会相等,则飞镖落在阴影区域的概率为( )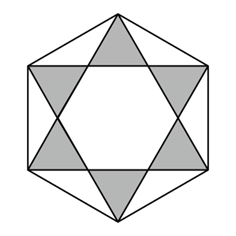 A、 B、 C、 D、8. 如图,若方格纸中每个小正方形的边长均为1,则阴影部分的面积为( )
A、 B、 C、 D、8. 如图,若方格纸中每个小正方形的边长均为1,则阴影部分的面积为( ) A、5 B、6 C、 D、
A、5 B、6 C、 D、二、填空题
-
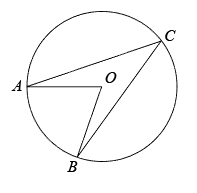
9. 因式分解: .10. 正十二边形每个内角的度数为 .11. 方程 的解是x= .12. 我国2021年粮食产量约为13700亿斤,创历史新高,其中13700亿斤用科学记数法表示为亿斤.13. 如图,A、B、C点在圆O上, 若∠ACB=36°, 则∠AOB= .
 14. 如图,圆锥的母线AB=6,底面半径CB=2,则其侧面展开图扇形的圆心角α=.
14. 如图,圆锥的母线AB=6,底面半径CB=2,则其侧面展开图扇形的圆心角α=.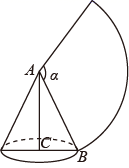 15. 若一元二次方程x2+x-c=0没有实数根,则c的取值范围是 .16. 如图,将矩形纸片ABCD沿CE折叠,使点B落在边AD上的点F处.若点E在边AB上,AB=3,BC=5,则AE= .
15. 若一元二次方程x2+x-c=0没有实数根,则c的取值范围是 .16. 如图,将矩形纸片ABCD沿CE折叠,使点B落在边AD上的点F处.若点E在边AB上,AB=3,BC=5,则AE= .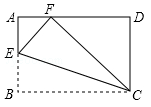 17. 若一次函数y=kx+b的图象如图所示,则关于kx+b>0的不等式的解集为 .
17. 若一次函数y=kx+b的图象如图所示,则关于kx+b>0的不等式的解集为 . 18. 若二次函数的图象上有且只有三个点到x轴的距离等于m,则m的值为 .
18. 若二次函数的图象上有且只有三个点到x轴的距离等于m,则m的值为 .三、解答题
-
19. 计算:(1)、;(2)、 .20.(1)、解方程:;(2)、解不等式组:21. 如图,将下列3张扑克牌洗匀后数字朝下放在桌面上.


 (1)、从中随机抽取1张,抽得扑克牌上的数字为3的概率为;(2)、从中随机抽取2张,用列表或画树状图的方法,求抽得2张扑克牌的数字不同的概率.22. 《孙子算经》是中国古代重要的数学著作,该书第三卷记载:“今有兽六首四足,禽四首二足,上有七十六首,下有四十六足,问禽、兽各几何?”译文:今有一种6头4脚的兽与一种4头2脚的鸟,若兽与鸟共有76个头与46只脚.问兽、鸟各有多少?
(1)、从中随机抽取1张,抽得扑克牌上的数字为3的概率为;(2)、从中随机抽取2张,用列表或画树状图的方法,求抽得2张扑克牌的数字不同的概率.22. 《孙子算经》是中国古代重要的数学著作,该书第三卷记载:“今有兽六首四足,禽四首二足,上有七十六首,下有四十六足,问禽、兽各几何?”译文:今有一种6头4脚的兽与一种4头2脚的鸟,若兽与鸟共有76个头与46只脚.问兽、鸟各有多少?根据译文,解决下列问题:
(1)、设兽有x个,鸟有y只,可列方程组为;(2)、求兽、鸟各有多少.23. 如图,在平行四边形ABCD中,点E、F在对角线BD上,且BE=DF.求证: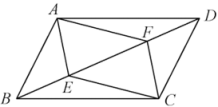 (1)、△ABE≌△CDF;(2)、四边形AECF是平行四边形.24. 如图,点A、B、C在圆O上,∠ABC=60°,直线AD∥BC,AB=AD,点O在BD上.
(1)、△ABE≌△CDF;(2)、四边形AECF是平行四边形.24. 如图,点A、B、C在圆O上,∠ABC=60°,直线AD∥BC,AB=AD,点O在BD上.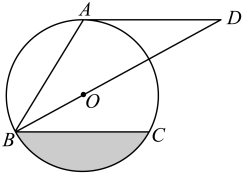 (1)、判断直线AD与圆O的位置关系,并说明理由;(2)、若圆的半径为6,求图中阴影部分的面积.25. 如图,下列装在相同的透明密封盒内的古钱币,其密封盒上分别标有古钱币的尺寸及质量,例如:钱币“文星高照”密封盒上所标“”是指该枚古钱币的直径为 , 厚度为 , 质量为 . 已知这些古钱币的材质相同.
(1)、判断直线AD与圆O的位置关系,并说明理由;(2)、若圆的半径为6,求图中阴影部分的面积.25. 如图,下列装在相同的透明密封盒内的古钱币,其密封盒上分别标有古钱币的尺寸及质量,例如:钱币“文星高照”密封盒上所标“”是指该枚古钱币的直径为 , 厚度为 , 质量为 . 已知这些古钱币的材质相同.
根据图中信息,解决下列问题.
(1)、这5枚古钱币,所标直径的平均数是 , 所标厚度的众数是 , 所标质量的中位数是 g;(2)、由于古钱币无法从密封盒内取出,为判断密封盒上所标古钱币的质量是否有错,桐桐用电子秤测得每枚古钱币与其密封盒的总质量如下:名称
文星高照
状元及第
鹿鹤同春
顺风大吉
连中三元
总质量/g
58.7
58.1
55.2
54.3
55.8
请你应用所学的统计知识,判断哪枚古钱币所标的质量与实际质量差异较大,并计算该枚古钱币的实际质量约为多少克.
26. 如图,公园内有一个垂直于地面的立柱AB,其旁边有一个坡面 , 坡角 . 在阳光下,小明观察到在地面上的影长为 , 在坡面上的影长为 . 同一时刻,小明测得直立于地面长60cm的木杆的影长为90cm(其影子完全落在地面上).求立柱AB的高度.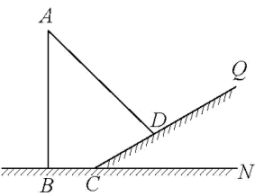 27. 如图,一次函数的图像与反比例函数的图像交于点 , 与轴交于点 , 与轴交于点 , 轴于点 , , 点关于直线的对称点为点 .
27. 如图,一次函数的图像与反比例函数的图像交于点 , 与轴交于点 , 与轴交于点 , 轴于点 , , 点关于直线的对称点为点 .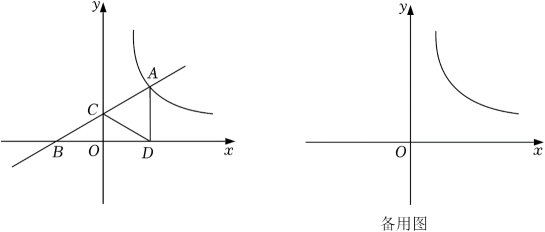 (1)、点是否在这个反比例函数的图象上?请说明理由;(2)、连接、 , 若四边形为正方形.
(1)、点是否在这个反比例函数的图象上?请说明理由;(2)、连接、 , 若四边形为正方形.①求、的值;
②若点在轴上,当最大时,求点的坐标.
28. 如图,在△ABC中,∠BAC=90°,AB=AC=12,点P在边AB上,D、E分别为BC、PC的中点,连接DE.过点E作BC的垂线,与BC、AC分别交于F、G两点.连接DG,交PC于点H.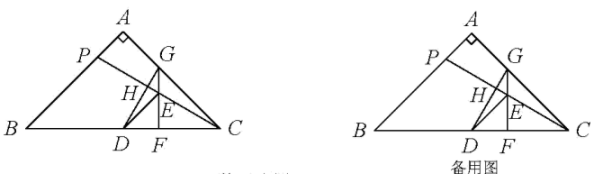 (1)、∠EDC的度数为;(2)、连接PG,求△APG 的面积的最大值;(3)、PE与DG存在怎样的位置关系与数量关系?请说明理由;(4)、求的最大值.
(1)、∠EDC的度数为;(2)、连接PG,求△APG 的面积的最大值;(3)、PE与DG存在怎样的位置关系与数量关系?请说明理由;(4)、求的最大值.