河南省鹤壁市淇滨区2022-2023学年八年级上学期素养提升(一)数学试题
试卷更新日期:2022-09-23 类型:月考试卷
一、单选题
-
1. 下列标志中,可以看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列实数是无理数的是( )A、 B、(π﹣1)0 C、2 D、3.143. 下列计算正确的是( )A、 B、 C、 D、4. 下列四个命题中,正确的个数有( )
2. 下列实数是无理数的是( )A、 B、(π﹣1)0 C、2 D、3.143. 下列计算正确的是( )A、 B、 C、 D、4. 下列四个命题中,正确的个数有( )①数轴上的点和有理数是一一对应的;②估计的值在 4 和 5 之间;③Rt△ABC 中,已知两边长分别是 3 和 4,则第三条边长为 5;④在平面直角坐标系中点(2,-3)关于x 轴对称的点的坐标是(2,3);⑤16 的平方根是±4 ,用式子表示是= ±4 ;⑥立方根等于它本身的数有2个.
A、1个 B、2个 C、3个 D、4个5. 如图,有四张不透明的卡片除正面不同外,其余完全相同,将它们背面朝上洗匀后,从中随机抽取一张,则抽到得卡片上算式正确的概率是( ) ;
; ;
; ;
; A、 B、 C、 D、16. 如图, , , 添加下列条件不能判定的是( )
A、 B、 C、 D、16. 如图, , , 添加下列条件不能判定的是( ) A、 B、 C、 D、7. 已知点P在第四象限内,且点P到x轴的距离是3.到y轴的距离是4.那么点P的坐标是( )A、(-4,3) B、(4,-3) C、(-3,4) D、(3, -4)8. 如图,将 纸片沿 折叠,使点 落在四边形 外点 的位置,则下列结论正确的是( )
A、 B、 C、 D、7. 已知点P在第四象限内,且点P到x轴的距离是3.到y轴的距离是4.那么点P的坐标是( )A、(-4,3) B、(4,-3) C、(-3,4) D、(3, -4)8. 如图,将 纸片沿 折叠,使点 落在四边形 外点 的位置,则下列结论正确的是( ) A、 B、 C、 D、9. 如图,所有阴影四边形都是正方形,所有三角形都是直角三角形,已知正方形A,B,C的面积依次为2,4,3,则正方形D的面积为( )
A、 B、 C、 D、9. 如图,所有阴影四边形都是正方形,所有三角形都是直角三角形,已知正方形A,B,C的面积依次为2,4,3,则正方形D的面积为( )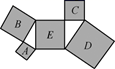 A、9 B、8 C、27 D、4510. 在同一坐标系中,函数 与 的大致图象是( )A、
A、9 B、8 C、27 D、4510. 在同一坐标系中,函数 与 的大致图象是( )A、 B、
B、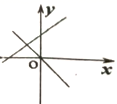 C、
C、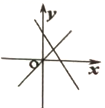 D、
D、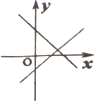
二、填空题
-
11. 2020年6月23日9时43分,“北斗三号”最后一颗全球组网卫星发射成功,它的授时精度小于 秒,则 用科学记数法表示为 .12. 已知 , 则自变量 x 的取值范围为 .13. 如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ACF=48°,则∠ABC的度数为=.
 14. 如图,两个正方形边长分别为a、b,如果a+b=17,ab=60,则阴影部分的面积为 .
14. 如图,两个正方形边长分别为a、b,如果a+b=17,ab=60,则阴影部分的面积为 . 15. 如图,在长方形中, , . 点、点分别在、上,且 , 点是边上的动点,点是边上的动点.则的是小值是 .
15. 如图,在长方形中, , . 点、点分别在、上,且 , 点是边上的动点,点是边上的动点.则的是小值是 .
三、解答题
-
16. 计算:(1)、;(2)、 .17.(1)、解方程:;(2)、已知实数 a ,b ,c ,d ,且 a ,b 互为倒数,c 的绝对值为 , d 的算术平方根是8,求 .18. 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC 的顶点A,C的坐标分别为(-4,5),(-1,3).

⑴请在如图所示的网格平面内作出平面直角坐标系;
⑵请作出△ABC 关于y轴对称的△;
⑶写出点的坐标;
⑷在y轴上找一点P,使得PB=PC.
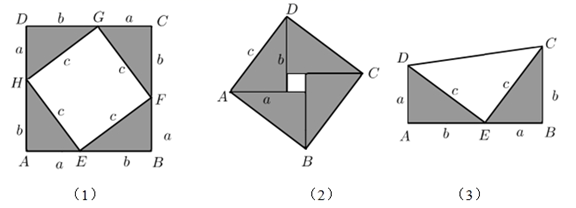
19. 为了减少二氧化碳的排放量,提倡绿色出行,越来越多市民选择租用共享单车出行,已知某共享单车公司为市民提供了手机支付(使用的前1小时免费)和会员卡支付两种支付方式,如图描述了两种方式应支付金额y(元)与骑行时间x(时)之间的函数关系,根据图象回答下列问题: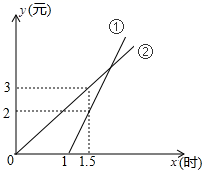 (1)、图中表示会员卡支付的收费方式是(填①或②).(2)、在图①中当x≥1时,求y与x的函数关系式.(3)、陈老师经常骑行该公司的共享单车,请根据不同的骑行时间帮他确定选择哪种支付方式比较合算.20. 勾股定理是毕达哥拉斯定理的中国称谓,它揭示了直角三角形三边的数量关系:直角三角形两直角边的平方和等于斜边的平方,中国是发现、研究和运用勾股定理最古老的国家之一,我国古称直角三角形的直角边为“勾”或“股”,斜边为“弦”,因而将这条定理称为勾股定理.请你从以下图形中,任意选择一个来证明这个定理.
(1)、图中表示会员卡支付的收费方式是(填①或②).(2)、在图①中当x≥1时,求y与x的函数关系式.(3)、陈老师经常骑行该公司的共享单车,请根据不同的骑行时间帮他确定选择哪种支付方式比较合算.20. 勾股定理是毕达哥拉斯定理的中国称谓,它揭示了直角三角形三边的数量关系:直角三角形两直角边的平方和等于斜边的平方,中国是发现、研究和运用勾股定理最古老的国家之一,我国古称直角三角形的直角边为“勾”或“股”,斜边为“弦”,因而将这条定理称为勾股定理.请你从以下图形中,任意选择一个来证明这个定理.
 21. 阅读材料:
21. 阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+2=(1+)2 . 善于思考的小明进行了以下探索:
设a+b=(m+n)2(其中a、b、m、n均为整数),则有a+b=m2+2n2+2mn.∴a=m2+2n2 , b=2mn.这样小明就找到了一种把类似a+b的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)、当a、b、m、n均为正整数时,若a+b=(m+n)2 , 用含m、n的式子分别表示a、b,得:a= , b=;(2)、利用所探索的结论,找一组正整数a、b、m、n填空:+=(+ )2;(3)、若a+6=(m+n)2 , 且a、m、n均为正整数,求a的值?