山东省枣庄市台儿庄区2021-2022学年九年级上学期期中考试数学试题

试卷更新日期：2022-09-23 类型：期中考试

进入出卷网下载

一、单选题

1. 把方程 $x^{2} - 10 x = - 3$ 左边化成含有 $x$ 的完全平方式，其中正确的是（）

A、 $x^{2} - 10 x + {(- 5)}^{2} = 28$ B、 $x^{2} - 10 x + {(- 5)}^{2} = 22$ C、 $x^{2} + 10 x + 5^{2} = 22$ D、 $x^{2} - 10 x + 5 = 2$

查看试题解析
2. 如图，D、E、F分别是 $△ A B C$ 各边中点，则以下说法错误的是（）

A、 $△ B D E$ 和 $△ D C F$ 的面积相等 B、四边形 $A E D F$ 是平行四边形 C、若 $A B = B C$ ，则四边形 $A E D F$ 是菱形 D、若 $∠ A = 90 °$ ，则四边形 $A E D F$ 是矩形

查看试题解析
3. 小颖有两顶帽子，分别为红色和黑色，有三条围巾，分别为红色、黑色和白色，她随机拿出一顶帽子和一条围巾戴上，恰好为红色帽子和红色围巾的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{2}{3}$ C、 $\frac{1}{6}$ D、 $\frac{5}{6}$

查看试题解析
4. 如图，在平行四边形ABCD中，∠ABC的平分线交AC于点E ，交AD于点F ，交CD的延长线于点G ，若AF＝2FD ，则 $\frac{B E}{E G}$ 的值为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{3}{4}$

查看试题解析
5. 关于 $x$ 的一元二次方程 $(a + 2) x^{2} - 3 x + 1 = 0$ 有实数根，则 $a$ 的取值范围是（）

A、 $a \leq \frac{1}{4}$ 且 $a \neq - 2$ B、 $a \leq \frac{1}{4}$ C、 $a < \frac{1}{4}$ 且 $a \neq - 2$ D、 $a < \frac{1}{4}$

查看试题解析
6. 甲和乙两个几何体都是由大小相同的小立方块搭成，它们的俯视图如图，小正方形中数字表示该位置上的小立方块个数（）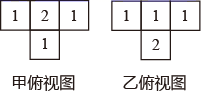

A、甲和乙左视图相同，主视图相同 B、甲和乙左视图不相同，主视图不相同 C、甲和乙左视图相同，主视图不相同 D、甲和乙左视图不相同，主视图相同

查看试题解析
7. 已知关于x的一元二次方程x²－kx＋k－3＝0的两个实数根分别为 $x_{1} ， x_{2}$ ，且 $x_{1}^{2} + x_{2}^{2} = 5$ ，则k的值是（）

A、－2 B、2 C、－1 D、1

查看试题解析
8. 如图，正方形ABCD的对角线AC，BD交于点O，M是边AD上一点，连接OM，过点O作ON⊥OM，交CD于点N．若四边形MOND的面积是1，则AB的长为（）

A、1 B、 $\sqrt{2}$ C、2 D、 $2 \sqrt{2}$

查看试题解析
9. 若菱形ABCD的一条对角线长为8，边CD的长是方程x²﹣10x+24＝0的一个根，则该菱形ABCD的周长为（）

A、16 B、24 C、16或24 D、48

查看试题解析
10. 如图，将 $△ A B C$ 沿 $B C$ 边向右平移得到 $△ D E F$ ， $D E$ 交 $A C$ 于点G.若 $B C ： E C = 3 ： 1$ . $S_{△ A D G} = 16$ .则 $S_{△ C E G}$ 的值为（）

A、2 B、4 C、6 D、8

查看试题解析
11. 若实数k、b是一元二次方程 $(x + 3) (x - 1) = 0$ 的两个根，且 $k < b$ ，则一次函数 $y = k x + b$ 的图象不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
12. 如图，在菱形ABCD中，点E、F分别是边BC、CD的中点，连接AE、AF、EF．若菱形ABCD的面积为16，则△AEF的面积为（）

A、3 B、4 C、5 D、6

查看试题解析

二、填空题

13. 若 $\frac{b}{a} = \frac{d}{c} = \frac{1}{2} (a \neq c)$ ，则 $\frac{b - d}{a - c} =$ ．

查看试题解析
14. 已知x= $2 + \sqrt{3}$ 是关于x的方程 $x^{2} - 4 x + m = 0$ 的一个根，则m＝.

查看试题解析
15. 贵阳市2021年中考物理实验操作技能测试中，要求学生两人一组合作进行，并随机抽签决定分组.有甲、乙、丙、丁四位同学参加测试，则甲、乙两位同学分到同一组的概率是.

查看试题解析
16. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，过点B作 $B D ⊥ C B$ ，垂足为B ，且 $B D = 3$ ，连接CD ，与AB相交于点M ，过点M作 $M N ⊥ C B$ ，垂足为N ．若 $A C = 2$ ，则MN的长为．

查看试题解析
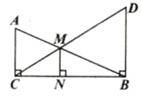17. 如图，BD是正方形ABCD的一条对角线，E是BD上一点，F是CB延长线上一点，连接CE ， EF ， AF ．若 $D E = D C$ ， $E F = E C$ ，则 $∠ B A F$ 的度数为．

查看试题解析
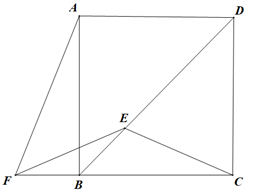18. 根据图中数字的规律，若第n个图中的q＝143，则p的值为．

查看试题解析

三、解答题

19. 解方程

(1)、 $x^{2} - 2 x = 2 x - 1$

(2)、 $3 x^{2} - 2 x - 5 = 0$ （配方法）

查看试题解析
20. 为了丰富校园文化生活，提高学生的综合素质，促进中学生全面发展，学校开展了多种社团活动.小明喜欢的社团有：合唱社团、足球社团、书法社团、科技社团（分别用字母A，B，C，D依次表示这四个社团），并把这四个字母分别写在四张完全相同的不透明的卡片的正面上，然后将这四张卡片背面朝上洗匀后放在桌面上.

(1)、小明从中随机抽取一张卡片是足球社团B的概率是.

(2)、小明先从中随机抽取一张卡片，记录下卡片上的字母后不放回，再从剩余的卡片中随机抽取一张卡片，记录下卡片上的字母.请你用列表法或画树状图法求出小明两次抽取的卡片中有一张是科技社团D的概率.

查看试题解析
21. 如图，在边长为1的正方形网格中建立平面直角坐标系，已知△ABC三个顶点分别为A（﹣1，2）、B（2，1）、C（4，5）．

(1)、以原点O为位似中心，在x轴的上方画出△A₁B₁C₁ ，使△A₁B₁C₁与△ABC位似，且相似比为2；

(2)、△A₁B₁C₁的面积是平方单位．

(3)、点P（a ， b）为△ABC内一点，则在△A₁B₁C₁内的对应点P’的坐标为．

查看试题解析
22. 如图，在菱形ABCD中，点E，F分别是边AD，AB的中点.

(1)、求证：△ABE≌△ADF；

(2)、若BE＝ $\sqrt{3}$ ，∠C＝60°，求菱形ABCD的面积.

查看试题解析
23. 实践与探究

(1)、操作一：如图①，已知正方形纸片ABCD，将正方形纸片沿过点A的直线折叠，使点B落在正方形ABCD的内部，点B的对应点为点M，折痕为AE，再将纸片沿过点A的直线折叠，使AD与AM重合，折痕为AF，则 $∠ E A F =$ 度.

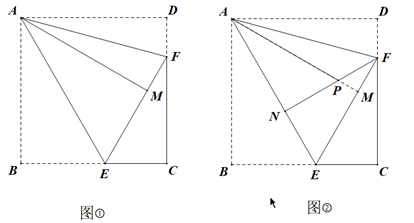
操作二：如图②，将正方形纸片沿EF继续折叠，点C的对应点为点N.我们发现，当点E的位置不同时，点N的位置也不同.当点E在BC边的某一位置时，点N恰好落在折痕AE上，则 $∠ A E F =$ 度.

(2)、在图②中，运用以上操作所得结论，解答下列问题：
设AM与NF的交点为点P.求证 $△ A N P ≌ △ F N E$ ：.

(3)、若 $A B = \sqrt{3}$ ，则线段AP的长为.

查看试题解析
24. 泰兴鑫都小商品市场以每副60元的价格购进800副羽毛球拍．九月份以单价100元销售，售出了200副．十月份如果销售单价不变，预计仍可售出200副．鑫都小商品市场为增加销售量，决定降价销售．根据市场调查，销售单价每降低5元，可多售出10副，但最低销售单价应高于购进的价格．十月份结束后，批发商将对剩余的羽毛球拍一次性清仓，清仓时销售单价为50元．设十月份销售单价降低x元．

(1)、填表：
月份
九月
十月
清仓
销售单价(元)
100
50
销售量(件)
200

(2)、如果鑫都小商品市场希望通过销售这批羽毛球拍获利9200元，那么十月份的销售单价应是多少元？

查看试题解析
25. 如图，在平行四边形ABCD中，AB＝3，点E为线段AB的三等分点（靠近点A），点F为线段CD的三等分点（靠近点C），且CE⊥AB．将△BCE沿CE对折，BC边与AD边交于点G，且DC＝DG．

(1)、证明：四边形AECF为矩形；

(2)、求四边形AECG的面积．

查看试题解析

月份	九月	十月	清仓
销售单价(元)	100		50
销售量(件)	200