山东省烟台市2021-2022学年九年级上学期期中数学试题
试卷更新日期:2022-09-23 类型:期中考试
一、单选题
-
1. 下列各点中在反比例函数y=﹣的图象上的是( )A、(﹣2,1) B、(1,﹣2) C、(﹣ , 1) D、( , ﹣2)2. 若用我们数学课本上采用的科学计算器计算 , 按键顺序正确的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列函数中,一定是二次函数是( )A、y=ax2+bx+c B、y=x(﹣x+1) C、y=(x﹣1)2﹣x2 D、y=4. 在 中, ,则 的正弦值为( )A、 B、 C、2 D、5. 已知一次函数的图像经过一、二、四象限,则下列关于反比例函数的描述,其中正确的是( )A、图象在一、三象限 B、随x的增大而减小 C、随x的增大而增大 D、当时,6. 将抛物线 向下平移2个单位,再向右平移3个单位,则平移后抛物线的函数表达式为( )A、 B、 C、 D、7. 如图,在 的正方形网格图中,小正方形的边长为1, 的顶点均在格点上,则下列关于 的说法错误的是( )
3. 下列函数中,一定是二次函数是( )A、y=ax2+bx+c B、y=x(﹣x+1) C、y=(x﹣1)2﹣x2 D、y=4. 在 中, ,则 的正弦值为( )A、 B、 C、2 D、5. 已知一次函数的图像经过一、二、四象限,则下列关于反比例函数的描述,其中正确的是( )A、图象在一、三象限 B、随x的增大而减小 C、随x的增大而增大 D、当时,6. 将抛物线 向下平移2个单位,再向右平移3个单位,则平移后抛物线的函数表达式为( )A、 B、 C、 D、7. 如图,在 的正方形网格图中,小正方形的边长为1, 的顶点均在格点上,则下列关于 的说法错误的是( )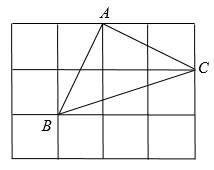 A、是直角三角形 B、tam C、面积为 D、 边上的高为8. 如图,已知点 , , 是轴上位于点上方的一点,平分 , 平分 , 直线交于点 . 若反比例函数的图像经过点 , 则的值是( )
A、是直角三角形 B、tam C、面积为 D、 边上的高为8. 如图,已知点 , , 是轴上位于点上方的一点,平分 , 平分 , 直线交于点 . 若反比例函数的图像经过点 , 则的值是( ) A、-8 B、-9 C、-10 D、-129. 已知点A(x1 , y1),B(x2 , y2)都在反比例函数y=﹣的图象上,且x1<0<x2 , 则y1 , y2的关系是( )A、y2<0<y1 B、0<y2<y1 C、y1<y2<0 D、y1<0<y210. 已知二次函数y=x2﹣2ax+5,当3≤x≤7时,y在x=7取得最大值,则实数a的取值范围是( )A、a≤3 B、a≤5 C、3≤a≤5 D、a≥511. 如图,某栋教学楼AB顶部竖有一块宣传牌BC,某同学从建筑物底端A点出发,沿水平方向向右走12米到达D点,在D处测得宣传牌底部B点的仰角是54°,再经过一段坡比为1:2.4,坡长为6.5米的斜坡DE到达E点(A、B、C、D、E均在同一平面内),在E处测得宣传牌的顶部C点的仰角是45°,则宣传牌BC的高度为( )(参考数据:sin54°≈0.80,cos54°≈0.59,tan54°≈1.38,结果精确到0.1米)
A、-8 B、-9 C、-10 D、-129. 已知点A(x1 , y1),B(x2 , y2)都在反比例函数y=﹣的图象上,且x1<0<x2 , 则y1 , y2的关系是( )A、y2<0<y1 B、0<y2<y1 C、y1<y2<0 D、y1<0<y210. 已知二次函数y=x2﹣2ax+5,当3≤x≤7时,y在x=7取得最大值,则实数a的取值范围是( )A、a≤3 B、a≤5 C、3≤a≤5 D、a≥511. 如图,某栋教学楼AB顶部竖有一块宣传牌BC,某同学从建筑物底端A点出发,沿水平方向向右走12米到达D点,在D处测得宣传牌底部B点的仰角是54°,再经过一段坡比为1:2.4,坡长为6.5米的斜坡DE到达E点(A、B、C、D、E均在同一平面内),在E处测得宣传牌的顶部C点的仰角是45°,则宣传牌BC的高度为( )(参考数据:sin54°≈0.80,cos54°≈0.59,tan54°≈1.38,结果精确到0.1米) A、1.4米 B、3.9米 C、4.0米 D、16.6米12. 如图,抛物线过点 , 且对称轴为直线 , 有下列结论①;②:③抛物线经过点与点 , 则;④无论a,b,c取何值,抛物线都经过同一个点;⑤ , 其中正确的结论是( )
A、1.4米 B、3.9米 C、4.0米 D、16.6米12. 如图,抛物线过点 , 且对称轴为直线 , 有下列结论①;②:③抛物线经过点与点 , 则;④无论a,b,c取何值,抛物线都经过同一个点;⑤ , 其中正确的结论是( ) A、①②③ B、③④⑤ C、②③④ D、②④⑤
A、①②③ B、③④⑤ C、②③④ D、②④⑤二、填空题
-
13. 当函数是二次函数时,a的值为 .14. 如图,已知公路l上A,B两点之间的距离为20米,点B在C的南偏西30°的方向上,A在C的南偏西60°方向上,则点C到公路l的距离为米.
 15. 如图,在四边形ABCD中, , , , , . 则四边形ABCD的面积为 .
15. 如图,在四边形ABCD中, , , , , . 则四边形ABCD的面积为 . 16. 如图,在平面直角坐标系中,矩形OADB顶点A、B分别在x轴、y轴的正半轴上,顶点D在函数 (x>0)的图象上.点P是矩形OADB内的一点,连接PA、PB、PD、PO,则图中阴影部分的面积是 .
16. 如图,在平面直角坐标系中,矩形OADB顶点A、B分别在x轴、y轴的正半轴上,顶点D在函数 (x>0)的图象上.点P是矩形OADB内的一点,连接PA、PB、PD、PO,则图中阴影部分的面积是 . 17. 如图,在x轴上有一点A(3,0),点D是点A关于y轴的对称点,点B在反比例函数的图象上,连接BD,交反比例函数图象于点C,若 , 的面积是24.则k的值是 .
17. 如图,在x轴上有一点A(3,0),点D是点A关于y轴的对称点,点B在反比例函数的图象上,连接BD,交反比例函数图象于点C,若 , 的面积是24.则k的值是 .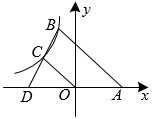 18. 如图,二次函数y=x2﹣4x+3图象与x轴的交点为A,与直线y=kx+b交于点B(4,3),则当x2﹣4x+3>kx+b时,自变量x的取值范围是 .
18. 如图,二次函数y=x2﹣4x+3图象与x轴的交点为A,与直线y=kx+b交于点B(4,3),则当x2﹣4x+3>kx+b时,自变量x的取值范围是 .
三、解答题
-
19. 计算:(1)、(2)、20. 根据下列条件,分别求出对应的二次函数表达式:(1)、已知图象的顶点坐标是(2,1),且与x轴的一个交点坐标是(3,0);(2)、已知图象经过 , , (3,10)三点;(3)、已知图象的对称轴为直线 , 顶点在x轴上,且经过点 .21. 如图,一次函数的图象与反比例函数的图象相交于点、 , 其中点.
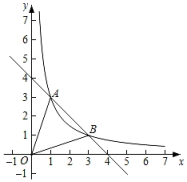 (1)、求该反比例函数的解析式;(2)、求△ABO的面积.22. 如图,矩形中,是边上一动点,过点的反比例函数的图象与边相交于点 .
(1)、求该反比例函数的解析式;(2)、求△ABO的面积.22. 如图,矩形中,是边上一动点,过点的反比例函数的图象与边相交于点 . (1)、点运动到边的中点时,求反比例函数的表达式;(2)、连接 , 求的值.23. 近年来,无人机航拍测量的应用越来越广泛.如图,无人机从A处观测某建筑物至高点O时,俯角为37°;继续水平前行10米到达B处,观测点O,此时的俯角为45°,已知无人机的水平飞行高度为45米.求这栋楼的高度是多少米.(结果精确到0.1)(参考数据:sin37°≈0.60,cos37°≈0.79,tan37°≈0.75,≈1.41)
(1)、点运动到边的中点时,求反比例函数的表达式;(2)、连接 , 求的值.23. 近年来,无人机航拍测量的应用越来越广泛.如图,无人机从A处观测某建筑物至高点O时,俯角为37°;继续水平前行10米到达B处,观测点O,此时的俯角为45°,已知无人机的水平飞行高度为45米.求这栋楼的高度是多少米.(结果精确到0.1)(参考数据:sin37°≈0.60,cos37°≈0.79,tan37°≈0.75,≈1.41) 24. 某城门的截面由一段抛物线和一个正方形(OMNE为正方形)的三条边围成,已知城门宽度为4米,最高处距地面6米.如图1所示,现以O点为原点,OM所在的直线为x轴,OE所在的直线为y轴建立直角坐标系.
24. 某城门的截面由一段抛物线和一个正方形(OMNE为正方形)的三条边围成,已知城门宽度为4米,最高处距地面6米.如图1所示,现以O点为原点,OM所在的直线为x轴,OE所在的直线为y轴建立直角坐标系. (1)、求上半部分抛物线的函数表达式,并写出其自变量的取值范围;(2)、有一辆宽3米,高4.5米的消防车需要通过该城门,请问该消防车能否正常进入?(3)、为营造节日气氛,需要临时搭建一个矩形“装饰门”ABCD,该“装饰门”关于抛物线对称轴对称,如图2所示,其中AB,AD,CD为三根承重钢支架,A、D在抛物线上,B,C在地面上,已知钢支架每米70元,问搭建这样一个矩形“装饰门”,仅钢支架一项,最多需要花费多少元?25. 为满足市场需求,某服装超市在六月初购进一款短袖T恤衫,每件进价是80元,超市规定每件售价不得少于90元,根据调查发现:当售价定为90元时,每周可卖出600件,一件T恤衫售价每提高1元,每周要少卖出10件.(1)、试求出每周的销售量(件)与每件售价元之间的函数表达式;(不需要写出自变量取值范围)(2)、该服装超市每周想从这款T恤衫销售中获利8250元,又想尽量给客户实惠,该如何给这款T恤衫定价?(3)、超市管理部门要求这款T恤衫售价不得高于110元,则当每件T恤衫售价定为多少元,每周的销售利润最大?最大利润是多少?
(1)、求上半部分抛物线的函数表达式,并写出其自变量的取值范围;(2)、有一辆宽3米,高4.5米的消防车需要通过该城门,请问该消防车能否正常进入?(3)、为营造节日气氛,需要临时搭建一个矩形“装饰门”ABCD,该“装饰门”关于抛物线对称轴对称,如图2所示,其中AB,AD,CD为三根承重钢支架,A、D在抛物线上,B,C在地面上,已知钢支架每米70元,问搭建这样一个矩形“装饰门”,仅钢支架一项,最多需要花费多少元?25. 为满足市场需求,某服装超市在六月初购进一款短袖T恤衫,每件进价是80元,超市规定每件售价不得少于90元,根据调查发现:当售价定为90元时,每周可卖出600件,一件T恤衫售价每提高1元,每周要少卖出10件.(1)、试求出每周的销售量(件)与每件售价元之间的函数表达式;(不需要写出自变量取值范围)(2)、该服装超市每周想从这款T恤衫销售中获利8250元,又想尽量给客户实惠,该如何给这款T恤衫定价?(3)、超市管理部门要求这款T恤衫售价不得高于110元,则当每件T恤衫售价定为多少元,每周的销售利润最大?最大利润是多少?