山东省烟台市福山区2021-2022学年九年级上学期期中数学试题
试卷更新日期:2022-09-23 类型:期中考试
一、单选题
-
1. 如图,直线过点 , 则的值为( )
 A、 B、 C、 D、2. 关于二次函数的图象,下列结论正确的是( )A、开口向下 B、对称轴是直线 C、顶点纵坐标是-3 D、当时,函数值随值的增大而增大3. 如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )
A、 B、 C、 D、2. 关于二次函数的图象,下列结论正确的是( )A、开口向下 B、对称轴是直线 C、顶点纵坐标是-3 D、当时,函数值随值的增大而增大3. 如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )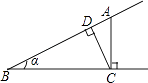 A、 B、 C、 D、4. 用计算器求 的值,以下按键顺序正确的是( )A、
A、 B、 C、 D、4. 用计算器求 的值,以下按键顺序正确的是( )A、 B、
B、 C、
C、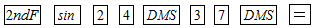 D、
D、 5. 某同学在用描点法画二次函数y=ax2+bx+c的图象时,列出了下面的表格:
5. 某同学在用描点法画二次函数y=ax2+bx+c的图象时,列出了下面的表格:x
…
﹣2
﹣1
0
1
2
…
y
…
﹣11
﹣2
1
﹣2
﹣5
…
由于粗心,他算错了其中一个y值,则这个错误的数值是( )
A、﹣11 B、﹣2 C、1 D、﹣56. 在同一平面直角坐标系内,二次函数 与一次函数 的图象可能是( )A、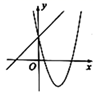 B、
B、 C、
C、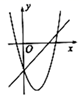 D、
D、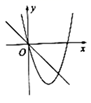 7. 已知二次函数y=2x2+bx+1,当b取不同的值时,其图象构成一个“抛物线系”,如图中的实线型抛物线分别是b取三个不同的值时二次函数的图象,它们的顶点在一条抛物线上(图中虚线型抛物线),则这条虚线型抛物线的解析式是( )
7. 已知二次函数y=2x2+bx+1,当b取不同的值时,其图象构成一个“抛物线系”,如图中的实线型抛物线分别是b取三个不同的值时二次函数的图象,它们的顶点在一条抛物线上(图中虚线型抛物线),则这条虚线型抛物线的解析式是( ) A、y=﹣x2+1 B、y=﹣2x2+1 C、y=﹣x2+1 D、y=﹣4x2+18. 数学活动课上,小敏、小颖分别画了△ABC和△DEF,数据如图,如果把小敏画的三角形面积记作S△ABC,小颖画的三角形面积记作S△DEF , 那么你认为( )
A、y=﹣x2+1 B、y=﹣2x2+1 C、y=﹣x2+1 D、y=﹣4x2+18. 数学活动课上,小敏、小颖分别画了△ABC和△DEF,数据如图,如果把小敏画的三角形面积记作S△ABC,小颖画的三角形面积记作S△DEF , 那么你认为( ) A、S△ABC >S△DEF B、S△ABC <S△DEF C、S△ABC =S△DEF D、不能确定9. 将二次函数的图象先向右平移2个单位,再向下平移3个单位,所得图象的函数解析式为 , 则、的值为( )A、 , B、 , C、 , D、 ,10. 如图,小明在某次投篮中,球的运动路线是抛物线y=﹣0.2x2+3.5的一部分,若命中篮圈中心,则他与篮圈底的距离l是( )
A、S△ABC >S△DEF B、S△ABC <S△DEF C、S△ABC =S△DEF D、不能确定9. 将二次函数的图象先向右平移2个单位,再向下平移3个单位,所得图象的函数解析式为 , 则、的值为( )A、 , B、 , C、 , D、 ,10. 如图,小明在某次投篮中,球的运动路线是抛物线y=﹣0.2x2+3.5的一部分,若命中篮圈中心,则他与篮圈底的距离l是( ) A、3m B、3.5m C、4m D、4.5m11. 如图,、、是小正方形的顶点,且每个小正方形的边长为1,则的值为( )
A、3m B、3.5m C、4m D、4.5m11. 如图,、、是小正方形的顶点,且每个小正方形的边长为1,则的值为( ) A、 B、 C、 D、无法求得12. 对称轴为直线x=1的抛物线 (a、b、c为常数,且a≠0)如图所示,小明同学得出了以下结论:①abc<0,②b2>4ac,③4a+2b+c>0,④3a+c>0,⑤a+b≤m(am+b)(m为任意实数), ⑥当x<-1时,y随x的增大而增大,其中结论正确的个数为( )
A、 B、 C、 D、无法求得12. 对称轴为直线x=1的抛物线 (a、b、c为常数,且a≠0)如图所示,小明同学得出了以下结论:①abc<0,②b2>4ac,③4a+2b+c>0,④3a+c>0,⑤a+b≤m(am+b)(m为任意实数), ⑥当x<-1时,y随x的增大而增大,其中结论正确的个数为( ) A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题
-
13. .14. 已知二次函数y=3x2+c的图象与正比例函数y=4x的图象只有一个交点,则c的值为 .15. 如图,人字梯AB,AC的长都为2米。当a=50°时,人字梯顶端高地面的高度AD是米(结果精确到0.1m。参考依据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
 16. 如图,一艘海轮位于灯塔的北偏东45方向,距离灯塔60海里的处,它沿正南方向航行一段时间后,到达位于灯塔的南偏东方向上的处,则此时船距灯塔的距离为海里.(结果保留根号)
16. 如图,一艘海轮位于灯塔的北偏东45方向,距离灯塔60海里的处,它沿正南方向航行一段时间后,到达位于灯塔的南偏东方向上的处,则此时船距灯塔的距离为海里.(结果保留根号) 17. 如图,小明在距离地面30米的P处测得A处的俯角为15°,B处的俯角为60°.若斜面坡度为1: ,则斜坡AB的长是米.
17. 如图,小明在距离地面30米的P处测得A处的俯角为15°,B处的俯角为60°.若斜面坡度为1: ,则斜坡AB的长是米.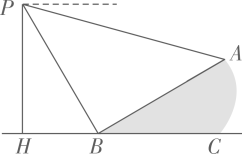 18. 二次函数的图象如图,点在轴的正半轴上,点 , 在二次函数的图象上,四边形为菱形,且 , 则菱形的面积为 .
18. 二次函数的图象如图,点在轴的正半轴上,点 , 在二次函数的图象上,四边形为菱形,且 , 则菱形的面积为 .
三、解答题
-
19. 先化简,再求值: , 其中 , .20. 如图,有长为的篱笆,现一面利用墙(墙的最大可用长度为)围成中间隔有一道篱笆的矩形花圃,设花圃的宽为 , 面积为 .
 (1)、求与的函数关系式,并写出的取值范围;(2)、如果围成花圃的面积为 , 那么应确定多长?21. 如图,甲楼高 , 在甲楼楼顶处、楼底处分别测得乙楼楼顶处的仰角为 , . , 垂足为点 . 求乙楼的高度 .
(1)、求与的函数关系式,并写出的取值范围;(2)、如果围成花圃的面积为 , 那么应确定多长?21. 如图,甲楼高 , 在甲楼楼顶处、楼底处分别测得乙楼楼顶处的仰角为 , . , 垂足为点 . 求乙楼的高度 . 22. 图1是电脑液晶显示器的侧面图,显示屏AB可以绕O点旋转一定角度,研究表明:如图2,当眼睛E与显示屏顶端A在同一水平线上,且望向显示器屏幕形成一个 俯角(即望向屏幕中心P的的视线EP与水平线EA的夹角)时,对保护眼睛比较好,而且显示屏顶端A与底座C的连线AC与水平线CD垂直时,观看屏幕最舒适,此时测得 ,液晶显示屏的宽AB为 .
22. 图1是电脑液晶显示器的侧面图,显示屏AB可以绕O点旋转一定角度,研究表明:如图2,当眼睛E与显示屏顶端A在同一水平线上,且望向显示器屏幕形成一个 俯角(即望向屏幕中心P的的视线EP与水平线EA的夹角)时,对保护眼睛比较好,而且显示屏顶端A与底座C的连线AC与水平线CD垂直时,观看屏幕最舒适,此时测得 ,液晶显示屏的宽AB为 .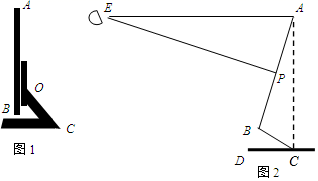 (1)、求眼睛E与显示屏顶端A的水平距离AE;(结果精确到 )(2)、求显示屏项端A与底座C的距离AC.(结果精确到 )(参考数据: )23. 如图,已知二次函数 的图象经过点 , ,与y轴交于点C.
(1)、求眼睛E与显示屏顶端A的水平距离AE;(结果精确到 )(2)、求显示屏项端A与底座C的距离AC.(结果精确到 )(参考数据: )23. 如图,已知二次函数 的图象经过点 , ,与y轴交于点C.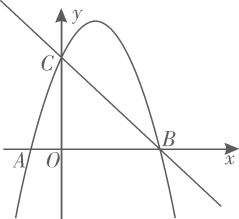 (1)、求抛物线的解析式;(2)、抛物线上是否存在点P,使 ,若存在请直接写出点P的坐标.若不存在,请说明理由.24. 某水果商店销售一种进价为40元/千克的优质水果,若售价为50元/千克,则一个月可售出500千克;若售价在50元/千克的基础上每涨价1元,则月销售量就减少10千克.(1)、当售价为55元/千克时,每月销售水果多少千克?(2)、当月利润为8750元时,每千克水果售价为多少元?(3)、当每千克水果售价为多少元时,获得的月利润最大?25. 如图,在平面直角坐标系中,以直线x=1为对称轴的抛物线与直线交于A(4,1),B两点,与y轴交于C(0,-1),直线与抛物线对称轴l交于点D.
(1)、求抛物线的解析式;(2)、抛物线上是否存在点P,使 ,若存在请直接写出点P的坐标.若不存在,请说明理由.24. 某水果商店销售一种进价为40元/千克的优质水果,若售价为50元/千克,则一个月可售出500千克;若售价在50元/千克的基础上每涨价1元,则月销售量就减少10千克.(1)、当售价为55元/千克时,每月销售水果多少千克?(2)、当月利润为8750元时,每千克水果售价为多少元?(3)、当每千克水果售价为多少元时,获得的月利润最大?25. 如图,在平面直角坐标系中,以直线x=1为对称轴的抛物线与直线交于A(4,1),B两点,与y轴交于C(0,-1),直线与抛物线对称轴l交于点D.
 (1)、求抛物线的函数关系式;(2)、若AD:BD=3:5,求直线AB的关系式;(3)、在(2)的条件下,在直线AB下方的抛物线上求点P的坐标,使△ABP的面积等于4;(4)、在(2)的条件下,在对称轴上求点Q,使得△ABQ是直角三角形.
(1)、求抛物线的函数关系式;(2)、若AD:BD=3:5,求直线AB的关系式;(3)、在(2)的条件下,在直线AB下方的抛物线上求点P的坐标,使△ABP的面积等于4;(4)、在(2)的条件下,在对称轴上求点Q,使得△ABQ是直角三角形.