山东省潍坊市寿光市2021-2022学年九年级上学期期中数学试题

试卷更新日期：2022-09-23 类型：期中考试

进入出卷网下载

一、单选题

1. 已知在Rt $△ A B C$ 中， $∠ C = 90^{°} ， \tan A = \frac{\sqrt{3}}{3}$ ，则 $∠ B$ 的度数是（）

A、 $30^{°}$ B、 $45^{°}$ C、 $60^{°}$ D、 $75^{°}$

查看试题解析
2. 如图，AB是⊙O直径，若∠AOC＝130°，则∠D的度数是（）

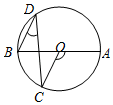A、20° B、25° C、40° D、50°

查看试题解析
3. 若关于x的一元二次方程x²+4x+m＝0有两个不相等的实数根，则m的取值范围是（）

A、m＞﹣4 B、m＞4 C、m≤﹣4 D、m＜4

查看试题解析
4. 如图，有一斜坡AB，坡顶B离地面的高度BC为30m，斜坡AB的坡度i＝1：2.5，则此斜坡的水平距离AC为（）

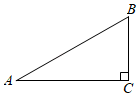A、75m B、50m C、30m D、12m

查看试题解析
5. 若 $x = 1$ 是一元二次方程 $(m + 3) x^{2} - m x + m^{2} - 12 = 0$ 的其中一个解，则 $m$ 的值为（）

A、3 B、-3 C、±3 D、2

查看试题解析
6. 如图，已知 $A B$ 是 $⊙ O$ 的直径， $B C$ 与 $⊙ O$ 相切于点 $B$ ，连接 $A C$ ， $O C$ ．若 $s i n ∠ B A C = \frac{1}{3}$ ，则 $t a n ∠ B O C$ 的值为（）

A、 $\frac{3}{4}$ B、 $\frac{1}{2}$ C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{\sqrt{3}}{3}$

查看试题解析
7. 某机械厂七月份生产零件100万个，第三季度生产零件392万个．设该厂八、九月份平均每月的增长率为x，那么x满足的方程是（）

A、100（1+x）²＝392 B、100+100（1+x）²＝392 C、100+100（1+x）+100（1+2x）＝392 D、100+100（1+x）+100（1+x）²＝392

查看试题解析
8. 如图，点A，B，C，D，E是⊙O上5个点，若AB＝AO＝2，将弧CD沿弦CD翻折，使其恰好经过点O，此时，图中阴影部分恰好形成一个“钻戒型”的轴对称图形，则“钻戒型”（阴影部分）的面积为（）

A、 $\frac{8 π}{3} - 3 \sqrt{3}$ B、4π﹣3 $\sqrt{3}$ C、4π﹣4 $\sqrt{3}$ D、 $\frac{8 π}{3} - 4 \sqrt{3}$

查看试题解析

二、多选题

9. 下列说法中，正确的有（）

A、等弧所对的圆心角相等 B、经过三点可以作一个圆 C、平分弦的直径垂直于这条弦 D、圆的内接平行四边形是矩形

查看试题解析
10. 数学课外兴趣小组的同学们要测量被池塘隔开的两棵树A，B的距离，他们设计了如图的测量方案：从树A沿着垂直于AB的方向走到E，再从E沿着垂直于AE的方向走到F，C为AE上一点，其中4位同学分别测得四组数据：其中能根据所测数据求出A，B两树距离的有（）

A、AC，∠ACB B、EF，DE，∠F C、CD，∠ACB，∠ADB D、∠F，∠ADB，FB

查看试题解析
11. 等腰三角形三边长分别为a，b，3，且a，b是关于x的一元二次方程x²﹣8x﹣1+m＝0的两根，则m的值为（）

A、15 B、16 C、17 D、18

查看试题解析
12. 如图，在△ABC中，∠C＝90°，AB＝5cm，cosB＝ $\frac{4}{5}$ ．动点D从点A出发沿着射线AC的方向以每秒1cm的速度移动，动点E从点B出发沿着射线BA的方向以每秒2cm的速度移动．已知点D和点E同时出发，设它们运动的时间为t秒，连接BD．下列结论正确的有（）

A、BC＝4cm； B、当AD＝AB时，tan∠ABD＝2； C、以点B为圆心、BE为半径画⊙B，当t＝ $\frac{25}{19}$ 时，DE与⊙B相切； D、当∠CBD＝∠ADE时，t＝ $\frac{25}{11}$ ．

查看试题解析

三、填空题

13. 已知正六边形的半径为 $\sqrt{2}$ ，则此正六边形的面积为．

查看试题解析
14. 设α、β是方程x²+2x﹣2021＝0的两根，则α²+3α+β的值为．

查看试题解析
15. 如图，点I和O分别是△ABC的内心和外心，若∠AIB＝125°，则∠AOB的度数为．

查看试题解析
16. 如图，四边形AOBC是正方形，曲线CP₁P₂P₃⋅⋅⋅叫做“正方形的渐开线”，其中弧CP₁ ，弧P₁P₂ ，弧P₂P₃ ，弧P₃P₄的圆心依次按点A，O，B，C循环，点A的坐标为（2，0），按此规律进行下去，则点P₂₀₂₁的坐标为．

查看试题解析

四、解答题

17. 解下列方程：

(1)、x²﹣4x+3＝0；

(2)、4x²﹣8x+1＝0（用配方法）．

查看试题解析
18. 某驻村工作队，为带动群众增收致富，巩固脱贫攻坚成效，决定在该村山脚下，围一块面积为600m²的矩形试验茶园，便于成功后大面积推广．如图所示，茶园一面靠墙，墙长32m，另外三面用68m长的篱笆围成，其中一边开有一扇2m宽的门（不包括篱笆）．求这个茶园的长和宽．

查看试题解析
19. 如图，在△ABC中，∠C=90°，点D，E分别在边AC，AB上，BD平分∠ABC，DE⊥AB，AE=6，cos A= $\frac{3}{5}$ .求：

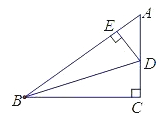(1)、DE，CD的长；

(2)、tan∠DBC的值．

查看试题解析
20. 如图，AB为⊙O的直径，C、D为圆上的两点，OC∥BD，OC交AD于点E．

(1)、求证：AC＝CD；

(2)、若OE＝2，AD＝8，求⊙O的半径．

查看试题解析
21. 如图，一艘渔船位于小岛 $B$ 的北偏东30°方向，距离小岛 $80 n mile$ 的点 $A$ 处，它沿着点 $A$ 的南偏东15°方向航行.

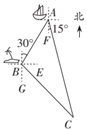(1)、渔船航行多远与小岛 $B$ 的距离最近？（结果保留根号）

(2)、渔船到达距离小岛 $B$ 最近点后，按原航向继续航行 $40 \sqrt{6} n mile$ 到点 $C$ 处时突然发生事故，渔船马上向小岛 $B$ 上的救援队求救，问：救援队从 $B$ 处出发沿着哪个方向航行到达事故地点航程最短，最短航程是多少？（结果保留根号）

查看试题解析
22. 定义：三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角．
如图1，∠E是△ABC中∠A的遥望角，如图2，四边形ABCD内接于⊙O， $\overset{⌢}{A D} = \overset{⌢}{B D}$ ，四边形ABCD的外角平分线DF交⊙O于点F，连接BF并延长交CD的延长线于点E．
求证：∠BEC是△ABC中∠BAC的遥望角．

查看试题解析
23. 如图，矩形ABCD ， AB＝6cm ， AD＝2cm ，点P以2cm/s的速度从顶点A出发沿折线A－B－C向点C运动，同时点Q以lcm/s的速度从顶点C出发向点D运动，当其中一个动点到达末端停止运动时，另一点也停止运动．

(1)、问两动点运动几秒，使四边形PBCQ的面积是矩形ABCD面积的 $\frac{4}{9}$ ；

(2)、问两动点经过多长时间使得点P与点Q之间的距离为 $\sqrt{5}$ ？若存在，
求出运动所需的时间；若不存在，请说明理由．

查看试题解析