山东省威海市文登区2021-2022学年九年级上学期期中数学试题
试卷更新日期:2022-09-23 类型:期中考试
一、单选题
-
1. 如图,在 中, , , ,若用科学计算器求AC的长,则下列按键顺序正确的是( )
 A、 B、 C、 D、2. 用计算器求 的值,以下按键顺序正确的是( )A、
A、 B、 C、 D、2. 用计算器求 的值,以下按键顺序正确的是( )A、 B、
B、 C、
C、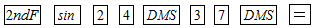 D、
D、 3. 如图,将 ABC放在每个小正方形的边长为1的网格中,点A,B,C均在格点上,则∠A的正切值是( )
3. 如图,将 ABC放在每个小正方形的边长为1的网格中,点A,B,C均在格点上,则∠A的正切值是( ) A、 B、 C、2 D、4. 已知二次函数 ,当 时,y随x增大而增大,则实数a的取值范围是( )A、 B、 C、 D、5. 下表中列出的是一个二次函数的自变量x与函数y的几组对应值:
A、 B、 C、2 D、4. 已知二次函数 ,当 时,y随x增大而增大,则实数a的取值范围是( )A、 B、 C、 D、5. 下表中列出的是一个二次函数的自变量x与函数y的几组对应值:…
-2
0
1
3
…
…
6
-4
-6
-4
…
下列各选项中,正确的是
A、这个函数的图象开口向下 B、这个函数的图象与x轴无交点 C、这个函数的最小值小于-6 D、当 时,y的值随x值的增大而增大6. 若二次函数 的图象如图所示,则一次函数 与反比例函数 在同一个坐标系内的大致图象为( )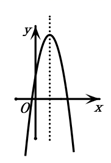 A、
A、 B、
B、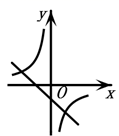 C、
C、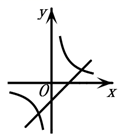 D、
D、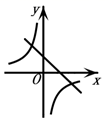 7. 如图,在 中, 于点D, .若E,F分别为 , 的中点,则 的长为( )
7. 如图,在 中, 于点D, .若E,F分别为 , 的中点,则 的长为( )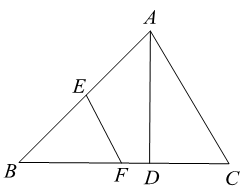 A、 B、 C、1 D、8. 将抛物线 的图象向右平移1个单位,再向下平移2个单位得到的抛物线必定经过( )A、 B、 C、 D、9. 二次函数y=x2+bx的图象如图,对称轴为直线x=1,若关于x的一元二次方程x2+bx﹣t=0(t为实数)在﹣1<x<4的范围内有解,则t的取值范围是( )
A、 B、 C、1 D、8. 将抛物线 的图象向右平移1个单位,再向下平移2个单位得到的抛物线必定经过( )A、 B、 C、 D、9. 二次函数y=x2+bx的图象如图,对称轴为直线x=1,若关于x的一元二次方程x2+bx﹣t=0(t为实数)在﹣1<x<4的范围内有解,则t的取值范围是( )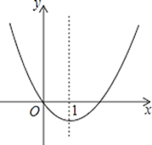 A、﹣1≤t<8 B、﹣1≤t<3 C、t≥﹣1 D、3<t<810. 如图中是抛物线形拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα= , tanβ= , 以O为原点,OA所在直线为x轴建立直角坐标系.若水面上升1m,水面宽为( )
A、﹣1≤t<8 B、﹣1≤t<3 C、t≥﹣1 D、3<t<810. 如图中是抛物线形拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα= , tanβ= , 以O为原点,OA所在直线为x轴建立直角坐标系.若水面上升1m,水面宽为( ) A、 B、 C、 D、11. 二次函数的部分图象如图所示,对称轴为 , 且经过点 . 下列说法:①;②;③;④若 , 是抛物线上的两点,则;⑤(其中).正确的结论有( )
A、 B、 C、 D、11. 二次函数的部分图象如图所示,对称轴为 , 且经过点 . 下列说法:①;②;③;④若 , 是抛物线上的两点,则;⑤(其中).正确的结论有( ) A、②③④ B、①②⑤ C、①③⑤ D、①②④⑤12. 如图,四边形 中, ,垂足分别为E,F,且 , .动点P,Q均以 的速度同时从点A出发,其中点P沿折线 运动到点B停止,点Q沿 运动到点B停止,设运动时间为 , 的面积为 ,则y与t对应关系的图象大致是( )
A、②③④ B、①②⑤ C、①③⑤ D、①②④⑤12. 如图,四边形 中, ,垂足分别为E,F,且 , .动点P,Q均以 的速度同时从点A出发,其中点P沿折线 运动到点B停止,点Q沿 运动到点B停止,设运动时间为 , 的面积为 ,则y与t对应关系的图象大致是( )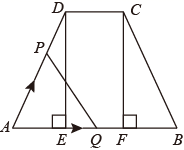 A、
A、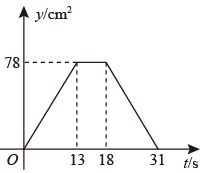 B、
B、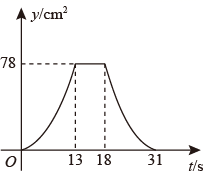 C、
C、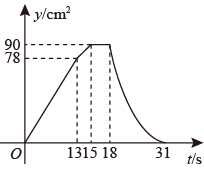 D、
D、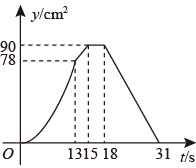
二、填空题
-
13. 函数的自变量x的取值范围是 .14. 如图,点A是反比例函数 的图象上一点,过点A作 轴于点C, 交反比例函数 的图象于点B,点P是y轴正半轴上一点.若 的面积为2,则k的值为.
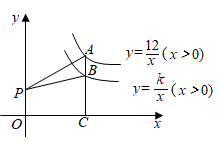 15. 从喷水池喷头喷出的水珠,在空中形成一条抛物线,如图所示,在抛物线各个位置上,水珠的竖直高度 (单位: )与它距离喷头的水平距离 (单位: )之间满足函数关系式 ,喷出水珠的最大高度是 .
15. 从喷水池喷头喷出的水珠,在空中形成一条抛物线,如图所示,在抛物线各个位置上,水珠的竖直高度 (单位: )与它距离喷头的水平距离 (单位: )之间满足函数关系式 ,喷出水珠的最大高度是 .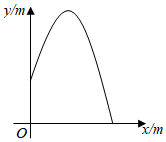 16. 如图,的顶点的坐标分别是 , 且 , 则顶点A的坐标是.
16. 如图,的顶点的坐标分别是 , 且 , 则顶点A的坐标是.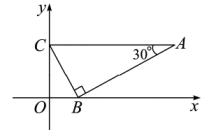 17. 小华用一张直角三角形纸片玩折纸游戏,如图1,在 中, , , .第一步,在 边上找一点 ,将纸片沿 折叠,点 落在 处,如图2,第二步,将纸片沿 折叠,点 落在 处,如图3.当点 恰好在原直角三角形纸片的边上时,线段 的长为.
17. 小华用一张直角三角形纸片玩折纸游戏,如图1,在 中, , , .第一步,在 边上找一点 ,将纸片沿 折叠,点 落在 处,如图2,第二步,将纸片沿 折叠,点 落在 处,如图3.当点 恰好在原直角三角形纸片的边上时,线段 的长为.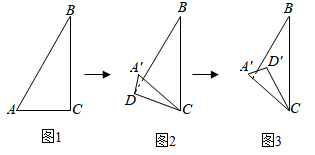 18. 如图,曲线AB是顶点为B,与y轴交于点A的抛物线y=﹣x2+4x+2的一部分,曲线BC是双曲线的一部分,由点C开始不断重复“A﹣B﹣C”的过程,形成一组波浪线,点P(2018,m)与Q(2020,n)均在该波浪线上,则mn= .
18. 如图,曲线AB是顶点为B,与y轴交于点A的抛物线y=﹣x2+4x+2的一部分,曲线BC是双曲线的一部分,由点C开始不断重复“A﹣B﹣C”的过程,形成一组波浪线,点P(2018,m)与Q(2020,n)均在该波浪线上,则mn= .
三、解答题
-
19.20. 如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA= , 求四边形ABCD的面积.
 21. 如图, 中, , ,点 ,点 ,反比例函数 的图象经过点A .
21. 如图, 中, , ,点 ,点 ,反比例函数 的图象经过点A .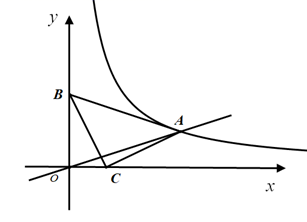 (1)、求反比例函数的解析式;(2)、将直线 向上平移m个单位后经过反比例函数,图象上的点 ,求m,n的值.22. 图1是疫情期间测温员用“额温枪”对小红测温时的实景图,图2是其侧面示意图,其中枪柄BC与手臂MC始终在同一直线上,枪身BA与额头保持垂直.量得胳膊MN=28cm,MB=42cm,肘关节M与枪身端点A之间的水平宽度为25.3cm(即MP的长度),枪身BA=8.5cm.(参考数据:sin66.4°≈0.92,cos66.4°≈0.40,sin23.6°≈0.40,)
(1)、求反比例函数的解析式;(2)、将直线 向上平移m个单位后经过反比例函数,图象上的点 ,求m,n的值.22. 图1是疫情期间测温员用“额温枪”对小红测温时的实景图,图2是其侧面示意图,其中枪柄BC与手臂MC始终在同一直线上,枪身BA与额头保持垂直.量得胳膊MN=28cm,MB=42cm,肘关节M与枪身端点A之间的水平宽度为25.3cm(即MP的长度),枪身BA=8.5cm.(参考数据:sin66.4°≈0.92,cos66.4°≈0.40,sin23.6°≈0.40,) (1)、求∠ABC的度数;(2)、测温时规定枪身端点A与额头距离范围为3~5cm.在图2中,若测得∠BMN=68.6°,小红与测温员之间距离为50cm.问此时枪身端点A与小红额头的距离是否在规定范围内?并说明理由.(结果保留小数点后一位)23. 小明投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=﹣10x+500,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.(1)、设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.(2)、当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?(3)、如果小明想要每月获得的利润不低于2000元,那么小明每月的成本最少需要多少元?(成本=进价×销售量)24. 甲秀楼是贵阳市一张靓丽的名片.如图①,甲秀楼的桥拱截面 可视为抛物线的一部分,在某一时刻,桥拱内的水面宽 ,桥拱顶点 到水面的距离是 .
(1)、求∠ABC的度数;(2)、测温时规定枪身端点A与额头距离范围为3~5cm.在图2中,若测得∠BMN=68.6°,小红与测温员之间距离为50cm.问此时枪身端点A与小红额头的距离是否在规定范围内?并说明理由.(结果保留小数点后一位)23. 小明投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=﹣10x+500,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.(1)、设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.(2)、当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?(3)、如果小明想要每月获得的利润不低于2000元,那么小明每月的成本最少需要多少元?(成本=进价×销售量)24. 甲秀楼是贵阳市一张靓丽的名片.如图①,甲秀楼的桥拱截面 可视为抛物线的一部分,在某一时刻,桥拱内的水面宽 ,桥拱顶点 到水面的距离是 .
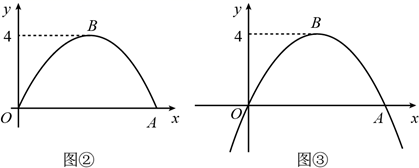 (1)、按如图②所示建立平面直角坐标系,求桥拱部分抛物线的函数表达式;(2)、一只宽为 的打捞船径直向桥驶来,当船驶到桥拱下方且距 点 时,桥下水位刚好在 处.有一名身高 的工人站立在打捞船正中间清理垃圾,他的头顶是否会触碰到桥拱,请说明理由(假设船底与水面齐平);(3)、如图③,桥拱所在的函数图象是抛物线 ,该抛物线在 轴下方部分与桥拱 在平静水面中的倒影组成一个新函数图象.将新函数图象向右平移 个单位长度,平移后的函数图象在 时, 的值随 值的增大而减小,结合函数图象,求 的取值范围.25. 如图所示,在坐标系xOy中,抛物线y=﹣x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=x+8经过A,C两点.
(1)、按如图②所示建立平面直角坐标系,求桥拱部分抛物线的函数表达式;(2)、一只宽为 的打捞船径直向桥驶来,当船驶到桥拱下方且距 点 时,桥下水位刚好在 处.有一名身高 的工人站立在打捞船正中间清理垃圾,他的头顶是否会触碰到桥拱,请说明理由(假设船底与水面齐平);(3)、如图③,桥拱所在的函数图象是抛物线 ,该抛物线在 轴下方部分与桥拱 在平静水面中的倒影组成一个新函数图象.将新函数图象向右平移 个单位长度,平移后的函数图象在 时, 的值随 值的增大而减小,结合函数图象,求 的取值范围.25. 如图所示,在坐标系xOy中,抛物线y=﹣x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=x+8经过A,C两点. (1)、求抛物线的解析式;(2)、在AC上方的抛物线上有一动点P.
(1)、求抛物线的解析式;(2)、在AC上方的抛物线上有一动点P.①如图1,当点P运动到某位置时,以AP,AO为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点P的坐标;
②如图2,过点O,P的直线y=kx(k<0)交AC于点E,若PE:OE=5:6,求k的值.