山东省威海乳山市(五四制)2021-2022学年九年级上学期期中考试数学试题
试卷更新日期:2022-09-23 类型:期中考试
一、单选题
-
1. 抛物线 的顶点坐标是( )A、 B、 C、 D、2. 在△ABC中,∠A,∠B都是锐角,且sinA= , cosB= , 则△ABC是( )A、直角三角形 B、钝角三角形 C、锐角三角形 D、等边三角形3. 已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:)是反比例函数关系,它的图象如图所示.下列说法正确的是( )
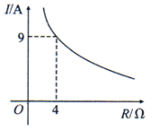 A、函数解析式为 B、蓄电池的电压是18V C、当时, D、当时,4. 抛物线的函数表达式为 ,若将 轴向上平移2个单位长度,将 轴向左平移3个单位长度,则该抛物线在新的平面直角坐标系中的函数表达式为( )A、 B、 C、 D、5. 某简易房的示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆AC的长为( )
A、函数解析式为 B、蓄电池的电压是18V C、当时, D、当时,4. 抛物线的函数表达式为 ,若将 轴向上平移2个单位长度,将 轴向左平移3个单位长度,则该抛物线在新的平面直角坐标系中的函数表达式为( )A、 B、 C、 D、5. 某简易房的示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆AC的长为( )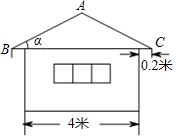 A、米 B、米 C、米 D、米6. 抛物线的顶点在坐标轴上,则b的值为( )A、6 B、±6 C、±6或0 D、07. 点 , , 都在反比例函数(为常数)的图象上,若 , 则 , , 的大小关系为( )A、 B、 C、 D、8. 如图,一艘船由 港沿北偏东65°方向航行 至 港,然后再沿北偏西40°方向航行至 港, 港在 港北偏东20°方向,则 , 两港之间的距离为( ) .
A、米 B、米 C、米 D、米6. 抛物线的顶点在坐标轴上,则b的值为( )A、6 B、±6 C、±6或0 D、07. 点 , , 都在反比例函数(为常数)的图象上,若 , 则 , , 的大小关系为( )A、 B、 C、 D、8. 如图,一艘船由 港沿北偏东65°方向航行 至 港,然后再沿北偏西40°方向航行至 港, 港在 港北偏东20°方向,则 , 两港之间的距离为( ) .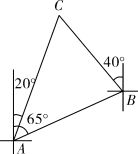 A、 B、 C、 D、9. 在平面直角坐标系中,抛物线 与 轴交于点 ,则该抛物线关于点 成中心对称的抛物线的表达式为( )A、 B、 C、 D、10. 如图,点A,B在反比例函数 (x>0)的图象上,点C、D在反比例函数 (k>0)的图象上,AC//BD//y轴,已知点A、B的横坐标分别为1、2,若△OAC与△ABD的面积之和为3,那么k的值是( )
A、 B、 C、 D、9. 在平面直角坐标系中,抛物线 与 轴交于点 ,则该抛物线关于点 成中心对称的抛物线的表达式为( )A、 B、 C、 D、10. 如图,点A,B在反比例函数 (x>0)的图象上,点C、D在反比例函数 (k>0)的图象上,AC//BD//y轴,已知点A、B的横坐标分别为1、2,若△OAC与△ABD的面积之和为3,那么k的值是( )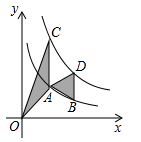 A、5 B、4 C、3 D、2
A、5 B、4 C、3 D、2二、多选题
-
11. 运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线.不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
t
0
1
2
3
4
5
6
7
…
h
0
8
14
18
20
20
18
14
…
下列结论正确的是( )
A、足球距离地面的最大高度为20m B、足球飞行路线的对称轴是直线 C、足球被踢出9s时落地 D、足球被踢出1.5s时,距离地面的高度是11m12. 二次函数y=ax2+bx+c(a≠0)的顶点坐标为(-1,n),其部分图象如图所示.下列结论正确的是( )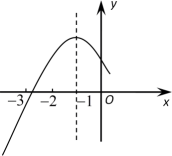 A、 B、 C、若 , 是抛物线上的两点,则 D、关于x的方程无实数根
A、 B、 C、若 , 是抛物线上的两点,则 D、关于x的方程无实数根三、填空题
-
13. 在Rt△ABC中,∠C= , , 则的值为.14. 抛物线y=ax2+bx+c(a≠0)的部分图象如图所示,其与x轴的一个交点坐标为(﹣3,0),对称轴为x=﹣1,则当y<0时,x的取值范围是.
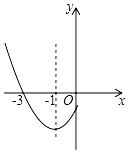 15. 如图,等边△ABO的顶点O与原点重合,点A的坐标是(-4,0),点B在第二象限.反比例函数的图象经过点B,则k的值是 .
15. 如图,等边△ABO的顶点O与原点重合,点A的坐标是(-4,0),点B在第二象限.反比例函数的图象经过点B,则k的值是 .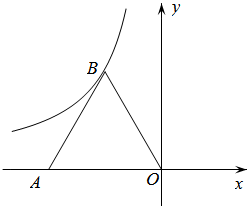 16. 如图1是一台手机支架,图2是其侧面示意图, , 可分别绕点A,B转动,测量知 , .当 , 转动到 , 时,点C到 的距离为cm.(结果保留小数点后一位,参考数据: , )
16. 如图1是一台手机支架,图2是其侧面示意图, , 可分别绕点A,B转动,测量知 , .当 , 转动到 , 时,点C到 的距离为cm.(结果保留小数点后一位,参考数据: , )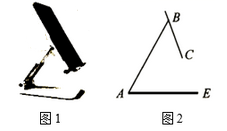 17. 如图,将Rt△ABO放置在直角坐标系中,OB边与x轴重合,AO=10, , 反比例函数(x<0)的图象经过AO的中点C,且与AB交于点D,则BD的长为 .
17. 如图,将Rt△ABO放置在直角坐标系中,OB边与x轴重合,AO=10, , 反比例函数(x<0)的图象经过AO的中点C,且与AB交于点D,则BD的长为 .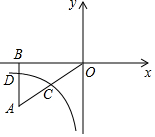 18. 如图,把抛物线y= x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y= x2交于点Q,则图中阴影部分的面积为 .
18. 如图,把抛物线y= x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y= x2交于点Q,则图中阴影部分的面积为 .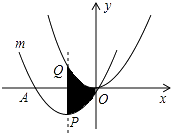
四、解答题
-
19. 计算:.20. 如图,在平面直角坐标系 中,一次函数 和 的图象相交于点 ,反比例函数 的图象经过点 .
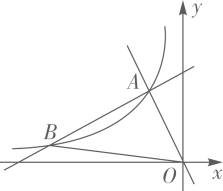 (1)、求反比例函数的表达式;(2)、设一次函数 的图象与反比例函数 的图象的另一个交点为 ,连接 ,求 的面积.21. 图①是甘肃省博物馆的镇馆之宝——铜奔马,又称“马踏飞燕”,于1969年10月出土于武威市的雷台汉墓,1983年10月被国家旅游局确定为中国旅游标志,在很多旅游城市的广场上都有“马踏飞燕”雕塑,某学习小组把测量本城市广场的“马踏飞燕”雕塑(图②)最高点离地面的高度作为一次课题活动,同学们制定了测量方案,并完成了实地测量,测得结果如下表:
(1)、求反比例函数的表达式;(2)、设一次函数 的图象与反比例函数 的图象的另一个交点为 ,连接 ,求 的面积.21. 图①是甘肃省博物馆的镇馆之宝——铜奔马,又称“马踏飞燕”,于1969年10月出土于武威市的雷台汉墓,1983年10月被国家旅游局确定为中国旅游标志,在很多旅游城市的广场上都有“马踏飞燕”雕塑,某学习小组把测量本城市广场的“马踏飞燕”雕塑(图②)最高点离地面的高度作为一次课题活动,同学们制定了测量方案,并完成了实地测量,测得结果如下表:课题
测量“马踏飞燕”雕塑最高点离地面的高度
测量示意图

如图,雕塑的最高点B到地面的高度为 ,在测点C用仪器测得点B的仰角为 ,前进一段距离到达测点E,再用该仪器测得点B的仰角为 ,且点A,B,C,D,E,F均在同一竖直平面内,点A,C,E在同一条直线上.
测量数据
的度数
的度数
的长度
仪器 ( )的高度
5米
米
请你根据上表中的测量数据,帮助该小组求出“马踏飞燕”雕塑最高点离地面的高度(结果保留一位小数).(参考数据: , , , , , )
 22. 某超市购进甲、乙两种商品,已知购进3件甲商品和2件乙商品共需60元;购进2件甲商品和3件乙商品共需65元.(1)、求甲、乙两种商品的进货单价分别是多少元?(2)、设甲商品的销售单价为x(单位:元/件).在销售过程中发现:当11≤x≤19时,甲商品的日销售量y(单位:件)与销售单价x之间存在一次函数关系,x与y之间的部分数值对应关系如下表:
22. 某超市购进甲、乙两种商品,已知购进3件甲商品和2件乙商品共需60元;购进2件甲商品和3件乙商品共需65元.(1)、求甲、乙两种商品的进货单价分别是多少元?(2)、设甲商品的销售单价为x(单位:元/件).在销售过程中发现:当11≤x≤19时,甲商品的日销售量y(单位:件)与销售单价x之间存在一次函数关系,x与y之间的部分数值对应关系如下表:销售单价x(元/件)
11
19
日销售量y(件)
18
2
若甲商品的日销售利润为w元,当甲商品的销售单价x(元/件)定为多少时,日销售利润最大?最大利润是多少?
23. 如图,一艘渔船位于小岛 的北偏东 方向,距离小岛 的点 处,它沿着点 的南偏东 的方向航行. (1)、渔船航行多远距离小岛 最近(结果保留根号)?(2)、渔船到达距离小岛 最近点后,按原航向继续航行 到点 处时突然发生事故,渔船马上向小岛 上的救援队求救,问救援队从 处出发沿着哪个方向航行到达事故地点航程最短,最短航程是多少(结果保留根号)?24. 如图,二次函数y=ax2+bx﹣3的图象交x轴于点A(﹣1,0),点B(3,0),交y轴于点C,抛物线的顶点为点M.
(1)、渔船航行多远距离小岛 最近(结果保留根号)?(2)、渔船到达距离小岛 最近点后,按原航向继续航行 到点 处时突然发生事故,渔船马上向小岛 上的救援队求救,问救援队从 处出发沿着哪个方向航行到达事故地点航程最短,最短航程是多少(结果保留根号)?24. 如图,二次函数y=ax2+bx﹣3的图象交x轴于点A(﹣1,0),点B(3,0),交y轴于点C,抛物线的顶点为点M.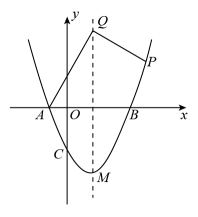 (1)、求二次函数的解析式;(2)、点P是抛物线上一点,设点P的横坐标为m(m>3),点Q在对称轴上,且AQ⊥PQ,若AQ=2PQ,求m的值.25. 如图1,点A(1,0),B(0,m)都在直线y=﹣2x+b上,四边形ABCD为平行四边形,点D在x轴上,AD=3,反比例函数(x>0)的图象经过点C.
(1)、求二次函数的解析式;(2)、点P是抛物线上一点,设点P的横坐标为m(m>3),点Q在对称轴上,且AQ⊥PQ,若AQ=2PQ,求m的值.25. 如图1,点A(1,0),B(0,m)都在直线y=﹣2x+b上,四边形ABCD为平行四边形,点D在x轴上,AD=3,反比例函数(x>0)的图象经过点C.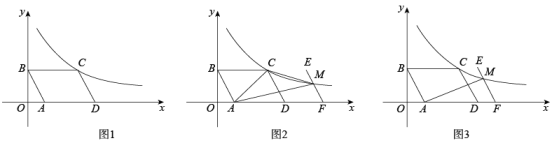 (1)、求k的值;(2)、将图1的线段CD向右平移n个单位长度(n≥0),得到对应线段EF,线段EF和反比例函数(x>0)的图象交于点M.
(1)、求k的值;(2)、将图1的线段CD向右平移n个单位长度(n≥0),得到对应线段EF,线段EF和反比例函数(x>0)的图象交于点M.①在平移过程中,如图2,若点M为EF的中点,求△ACM的面积;
②在平移过程中,如图3,若AM⊥EF,求n的值.