山东省日照市2021-2022学年九年级上学期期中数学试题
试卷更新日期:2022-09-23 类型:期中考试
一、单选题
-
1. 已知中,最长的弦长为16cm,则的半径是( )A、4cm B、8cm C、16cm D、32cm2. 下列四个命题中,真命题是( )A、相等的圆心角所对的两条弦相等 B、三角形的内心是到三角形三边距离相等的点 C、平分弦的直径一定垂直于这条弦 D、等弧就是长度相等的弧3. 已知⊙O的直径等于12cm,圆心O到直线l的距离为5cm,则直线l与⊙O的交点个数为()A、0 B、1 C、2 D、无法确定4. 一个不透明口袋中装有3个红球2个白球,除颜色外都相同,从中任意摸出一个球,下列叙述正确的是( )A、摸到红球是必然事件 B、摸到白球是不可能事件 C、摸到红球的可能性比白球大 D、摸到白球的可能性比红球大5. 用一个圆心角为120°,半径为3的扇形作一个圆锥的侧面,则这个圆锥的底面半径为( )A、 B、1 C、 D、26. 从长度分别为1、3、5、7的四条线段中任选三条作边,能构成三角形的概率为 ( )A、 B、 C、 D、7. 如图,AB是的直径,点C在上,连接AC、BC,过点O作交于点D,点C、D在AB的异侧.若 , 则的度数是( )
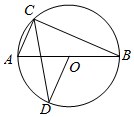 A、66° B、67° C、57° D、48°8. 如图,已知的半径为 , 弦直径 , , 则的长为( )
A、66° B、67° C、57° D、48°8. 如图,已知的半径为 , 弦直径 , , 则的长为( ) A、 B、 C、 D、9. 等边三角形的内切圆半径、外接圆半径和高的比为( )A、1∶∶ B、1∶2∶ C、1∶∶2 D、1∶2∶310. 如图,点B在⊙A上,点C在⊙A外,以下条件不能判定BC是⊙A切线的是( )
A、 B、 C、 D、9. 等边三角形的内切圆半径、外接圆半径和高的比为( )A、1∶∶ B、1∶2∶ C、1∶∶2 D、1∶2∶310. 如图,点B在⊙A上,点C在⊙A外,以下条件不能判定BC是⊙A切线的是( )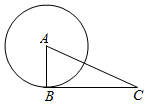 A、∠A=50°,∠C=40° B、∠B﹣∠C=∠A C、AB2+BC2=AC2 D、⊙A与AC的交点是AC中点11. 如图,△ABC中,∠C=90°,BC=5,⊙O与△ABC的三边相切于点D、E、F,若⊙O的半径为2,则△ABC的周长为( )
A、∠A=50°,∠C=40° B、∠B﹣∠C=∠A C、AB2+BC2=AC2 D、⊙A与AC的交点是AC中点11. 如图,△ABC中,∠C=90°,BC=5,⊙O与△ABC的三边相切于点D、E、F,若⊙O的半径为2,则△ABC的周长为( ) A、14 B、20 C、24 D、3012. 如图,在扇形AOB中, , 点C在上,且的长为 , 点D在OA上,连接BD,CD,若点C,O关于直线BD对称,则图中阴影部分的面积为( )
A、14 B、20 C、24 D、3012. 如图,在扇形AOB中, , 点C在上,且的长为 , 点D在OA上,连接BD,CD,若点C,O关于直线BD对称,则图中阴影部分的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 如图,AB是的直径,点C在上, . 则 .
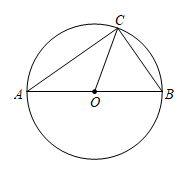 14. 如图,圆锥的母线长 , 底面圆的周长是 , 则圆锥的侧面积是 .
14. 如图,圆锥的母线长 , 底面圆的周长是 , 则圆锥的侧面积是 . 15. 一个不透明的袋子中装有黑、白小球各两个,这些小球除颜色外无其他差别,从袋子中随机摸出两个小球,则摸出的小球都是黑球的概率为.16. 如图,一个长为4,宽为3的长方形木板斜靠在水平桌面上的一个小方块上,其长边与水平桌面成30°夹角,将长方形木板按逆时针方向做两次无滑动的翻滚,使其长边恰好落在水平桌面l上,则木板上点A滚动所经过的路径长为.
15. 一个不透明的袋子中装有黑、白小球各两个,这些小球除颜色外无其他差别,从袋子中随机摸出两个小球,则摸出的小球都是黑球的概率为.16. 如图,一个长为4,宽为3的长方形木板斜靠在水平桌面上的一个小方块上,其长边与水平桌面成30°夹角,将长方形木板按逆时针方向做两次无滑动的翻滚,使其长边恰好落在水平桌面l上,则木板上点A滚动所经过的路径长为.
三、解答题
-
17. 如图,在平面直角坐标系中,、、 .
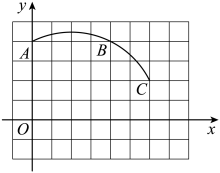 (1)、在图中画出经过A、B、C三点的圆弧所在圆的圆心M的位置.(2)、写出圆心点M的坐标为;(3)、若 , 判断点D与的位置关系.18. 如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.
(1)、在图中画出经过A、B、C三点的圆弧所在圆的圆心M的位置.(2)、写出圆心点M的坐标为;(3)、若 , 判断点D与的位置关系.18. 如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°. (1)、求证:DP是⊙O的切线;(2)、若⊙O的半径为3cm,求图中阴影部分的面积.19. 在一次数学兴趣小组活动中,小李和小王两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于11,则小李获胜;若指针所指区域内两数和大于11,则小王获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
(1)、求证:DP是⊙O的切线;(2)、若⊙O的半径为3cm,求图中阴影部分的面积.19. 在一次数学兴趣小组活动中,小李和小王两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于11,则小李获胜;若指针所指区域内两数和大于11,则小王获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止). (1)、请用列表或画树状图的方法分别求出小李和小王获胜的概率;(2)、这个游戏公平吗?若不公平,请你设计一个公平的游戏规则.20. 如图,四边形ABCD内接于⊙O , AD是直径,AC平分∠BAD , 过点C作⊙O的切线,与AB的延长线交于点E .
(1)、请用列表或画树状图的方法分别求出小李和小王获胜的概率;(2)、这个游戏公平吗?若不公平,请你设计一个公平的游戏规则.20. 如图,四边形ABCD内接于⊙O , AD是直径,AC平分∠BAD , 过点C作⊙O的切线,与AB的延长线交于点E . (1)、求证:∠E=90°;(2)、若⊙O的半径长为4,AC长为7,求BC的长;21. 如图,从一直径为1米的圆形铁皮中剪出一个圆心角为90度的最大扇形ABC.求:
(1)、求证:∠E=90°;(2)、若⊙O的半径长为4,AC长为7,求BC的长;21. 如图,从一直径为1米的圆形铁皮中剪出一个圆心角为90度的最大扇形ABC.求: (1)、剪掉后的剩余部分的面积;(2)、用所剪得的扇形ABC围成一个圆锥,该圆锥的底面半径是多少?(3)、如果从剪掉的部分中给圆锥配一个底,请问是否够用?22. 若一个四边形的两条对角线互相垂直且相等,则称这个四边形为“奇妙四边形”.如图1,四边形ABCD中,若AC=BD,AC⊥BD,则称四边形ABCD为奇妙四边形.根据“奇妙四边形”对角线互相垂直的特征可得“奇妙四边形”的一个重要性质:“奇妙四边形”的面积等于两条对角线乘积的一半.根据以上信息回答:
(1)、剪掉后的剩余部分的面积;(2)、用所剪得的扇形ABC围成一个圆锥,该圆锥的底面半径是多少?(3)、如果从剪掉的部分中给圆锥配一个底,请问是否够用?22. 若一个四边形的两条对角线互相垂直且相等,则称这个四边形为“奇妙四边形”.如图1,四边形ABCD中,若AC=BD,AC⊥BD,则称四边形ABCD为奇妙四边形.根据“奇妙四边形”对角线互相垂直的特征可得“奇妙四边形”的一个重要性质:“奇妙四边形”的面积等于两条对角线乘积的一半.根据以上信息回答: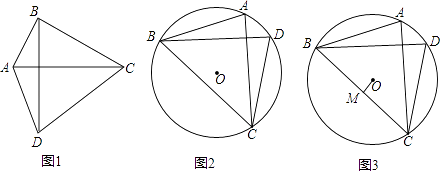 (1)、矩形 “奇妙四边形”(填“是”或“不是”);(2)、如图2,已知⊙O的内接四边形ABCD是“奇妙四边形”,若⊙O的半径为6,∠BCD=60°.求“奇妙四边形”ABCD的面积;(3)、如图3,已知⊙O的内接四边形ABCD是“奇妙四边形”作OM⊥BC于M.请猜测OM与AD的数量关系,并证明你的结论.
(1)、矩形 “奇妙四边形”(填“是”或“不是”);(2)、如图2,已知⊙O的内接四边形ABCD是“奇妙四边形”,若⊙O的半径为6,∠BCD=60°.求“奇妙四边形”ABCD的面积;(3)、如图3,已知⊙O的内接四边形ABCD是“奇妙四边形”作OM⊥BC于M.请猜测OM与AD的数量关系,并证明你的结论.