山东省青岛市即墨区2021-2022学年九年级上学期期中数学试题

试卷更新日期：2022-09-23 类型：期中考试

进入出卷网下载

一、单选题

1. 如果2是方程x²﹣3x+c=0的一个根，那么c的值是（）

A、4 B、﹣4 C、2 D、﹣2

查看试题解析
2. 有五张卡片的正面分别写有“我”“的”“中”“国”“梦”，五张卡片洗匀后将其反面放在桌面上，小明从中任意抽取两张卡片，恰好是“中国”的概率是(　　)

A、 $\frac{1}{10}$ B、 $\frac{1}{20}$ C、 $\frac{2}{25}$ D、 $\frac{1}{25}$

查看试题解析
3. 如图，l₁∥l₂∥l₃ ，直线a，b与l₁ ， l₂ ， l₃分别交于点A，B，C和点D，E，F．若 $\frac{A B}{B C} = \frac{2}{3}$ ， DE＝4，则DF的长是（）

A、 $\frac{8}{3}$ B、 $\frac{20}{3}$ C、6 D、10

查看试题解析
4.
如图，已知某广场菱形花坛ABCD的周长是24米，∠BAD=60°，则花坛对角线AC的长等于（　　）

A、6 $\sqrt{3}$ 米 B、6米 C、3 $\sqrt{3}$ 米 D、3米

查看试题解析
5. 李明去参加聚会，每两人都互相赠送礼物，他发现共送礼物30件，若设有n人参加聚会，根据题意可列出方程为（）

A、 $\frac{n (n + 1)}{2} = 30$ B、n（n﹣1）＝30 C、 $\frac{n (n - 1)}{2} =$ 30 D、n（n＋1）＝30

查看试题解析
6. 根据表格对应值：
x
1.1
1.2
1.3
1.4
ax²＋bx＋c
﹣0.59
0.84
2.29
3.76
判断关于x的方程ax²＋bx＋c＝2的一个解x的范围是（）

A、1.1＜x＜1.2 B、1.2＜x＜1.3 C、1.3＜x＜1.4 D、无法判定

查看试题解析
7. 如图，点P在△ABC的边AC上，要判断△ABP∽△ACB，添加一个条件，错误的是（）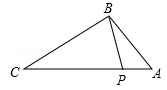

A、∠ABP=∠C B、∠APB=∠ABC C、 $\frac{A P}{A B} = \frac{A B}{A C}$ D、 $\frac{A B}{B P} = \frac{A C}{C B}$

查看试题解析
8. 如图，在矩形ABCD中，E是AD边的中点，BE⊥AC于点F，连接DF，下列四个结论：①△AEF∽△CAB；②CF＝2AF；③DF＝DC；④S_四边形_CDEF＝ $\frac{5}{2}$ S_△_ABF ．其中正确的结论有（）个

A、4 B、3 C、2 D、1

查看试题解析

二、填空题

9. 方程x²＝4x的根是．

查看试题解析
10. 若 $\frac{a}{3} = \frac{b}{4} = \frac{c}{5}$ ，则 $\frac{2 a - b}{c}$ ＝.

查看试题解析
11. 一个不透明的布袋中，装有红、白两种只有颜色不同的小球，其中红色小球有8个，为估计袋中白色小球的数目，每次将袋中小球搅匀后摸出一个小球记下颜色放回，再次搅匀…100次试验发现摸到红球20次，则估计白色小球的数目是个．

查看试题解析
12. 相邻两边长的比值是黄金分割数的矩形，叫作黄金矩形．从外形看，它最具美感．现在想要制作一张“黄金矩形”的贺年卡，如果较长的一条边长等于26厘米，那么相邻一条边的边长等于厘米．

查看试题解析
13. 如图，正方形ABCD和正方形CEFG中，点D在CG上，BC=2，CE=6，H是AF的中点，那么CH的长是．

查看试题解析
14. 如图，在△ABC中，BC＝16
如图甲，B₁是AB的中点，BC∥B₁C₁ ，则B₁C₁＝8
如图乙，B₁、B₂是AB的三等分点，BC∥B₁C₁∥B₂C₂ ，则B₁C₁＋B₂C₂＝；
如图丙，B₁、B₂、…、Bn是AB的（n＋1）等分点，BC∥B₁C₁∥B₂C₂∥…∥BnCn，则BC＋B₁C＋B₂C₂＋…＋BnCn＝．

查看试题解析

三、解答题

15. 小明想利用一块三角形纸片裁剪一个菱形，要求一个顶点为A，另外三个顶点分别在三角形的三边上，请你在原图上利用尺规作图把这个菱形作出来．

查看试题解析
16. 解方程

(1)、配方法解方程2x²﹣12x﹣12＝0；

(2)、（x＋2）（x＋3）＝1

查看试题解析
17. 已知关于x的一元二次方程（a﹣1）x²﹣2x＋1＝0有两个实数根，求a的非负整数解．

查看试题解析
18. 小颖和小丽做“摸球”游戏：在一个不透明的袋子中装有编号为1～4的四个球(除编号外都相同)，从中随机摸出一个球，记下数字后放回，再从中摸出一个球，记下数字．若两次数字之和大于5，则小颖胜，否则小丽胜．这个游戏对双方公平吗？请说明理由．

查看试题解析
19. 某公司今年销售一种产品，1月份获得利润20万元，由于产品畅销，利润逐月增加，3月份的利润比2月份的利润增加4.8万元，假设该产品利润每月的增长率相同．

(1)、求这个增长率；

(2)、求3月份的利润是多少万元？

查看试题解析
20. 如图，△ABC是等边三角形，CE是外角平分线，点D在AC上，连接BD并延长与CE交于点E

(1)、求证：△ABD∽△CED

(2)、若AB＝6，AD＝2CD，求BE的长．

查看试题解析
21. 如图，在▱ABCD中，点F是边BC的中点，连接AF并延长交DC的延长线于点E，连接AC、BE．

(1)、求证：AB＝CE；

(2)、若∠AFC＝2∠D，则四边形ABEC是什么特殊四边形？请说明理由

查看试题解析
22. 水果店老板以每斤2元的价格购进苹果若干斤，然后以每斤4元的价格出售，每天可售出100斤，通过调查发现，每斤苹果的售价每降低0.1元，每天可多售出20斤，为保证每天至少售出280斤，老板决定降价销售．

(1)、若每斤售价降低0.5元，则每天的销售量是斤．

(2)、若每斤售价降低x元，则每天的销售量是斤（用含x的代数式表示，需要化简）；

(3)、水果店老板要想通过销售苹果每天盈利300元，需将每斤苹果的售价定为多少元？

查看试题解析
23. 如图，正方形ABCD的四个顶点分别在正方形EFGH的四条边上，我们称正方形EFGH是正方形ABCD的外接正方形．
探究一：已知边长为1的正方形ABCD，是否存在一个外接正方形EFGH，它的面积是正方形ABCD面积的2倍？如图，假设存在正方形EFGH，它的面积是正方形ABCD的2倍．
因为正方形ABCD的面积为1，则正方形EFGH的面积为2，
所以EF＝FG＝GH＝HE＝ $\sqrt{2}$ ，设EB＝x，则BF＝ $\sqrt{2}$ ﹣x，
∵Rt△AEB≌Rt△BFC
∴BF＝AE＝ $\sqrt{2}$ ﹣x
在Rt△AEB中，由勾股定理，得
x²+（ $\sqrt{2}$ ﹣x）²＝1²
解得，x₁＝x₂＝ $\frac{\sqrt{2}}{2}$
∴BE＝BF，即点B是EF的中点．
同理，点C，D，A分别是FG，GH，HE的中点．
所以，存在一个外接正方形EFGH，它的面积是正方形ABCD面积的2倍
探究二：已知边长为1的正方形ABCD，是否存在一个外接正方形EFGH，它的面积是正方形ABCD面积的3倍？（仿照上述方法，完成探究过程）
探究三：已知边长为1的正方形ABCD， ▲ 一个外接正方形EFGH，它的面积是正方形ABCD面积的4倍？（填“存在”或“不存在”）
探究四：已知边长为1的正方形ABCD，是否存在一个外接正方形EFGH，它的面积是正方形ABCD面积的n倍？（n＞2）（仿照上述方法，完成探究过程）

查看试题解析
24. 如图，在矩形ABCD中，AB＝6cm，AD＝8cm，直线EF从点A出发沿AD方向匀速运动，速度是2cm/s，运动过程中始终保持EF∥AC，F交AD于E，交DC于点F，同时，点P从点C出发沿CB方向匀速运动，速度是1cm/s，连接PE、PF，设运动时间t（s）（0＜t＜4）．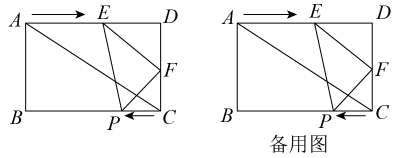

(1)、求t为何值时，四边形EPCD为矩形；

(2)、设△PEF的面积为S（cm²），求出面积S关于时间t的表达式；

(3)、在运动过程中，是否存在某一时刻使S_△PCF：S_矩形ABCD＝1：16？若存在，求出t的值；

(4)、是否存在某一时刻，使P在EF的垂直平分线上，若存在，求出t的值：若不存在，请说明理由．

查看试题解析

x	1.1	1.2	1.3	1.4
ax²＋bx＋c	﹣0.59	0.84	2.29	3.76