山东省临沂市沂南县2021-2022学年九年级上学期期中数学试题

试卷更新日期：2022-09-23 类型：期中考试

进入出卷网下载

一、单选题

1. 若 $x = 1$ 是方程 $x^{2} - a x - 1 = 0$ 的一个根，则a的值为（）

A、-1 B、0 C、11 D、2

查看试题解析
2. 下列图形中既是中心对称图形，又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 用配方法解方程 $x^{2} + 2 x - 2 = 0$ ，原方程应变形为（）

A、 ${(x + 1)}^{2} = 3$ B、 ${(x - 1)}^{2} = 3$ C、 ${(x + 1)}^{2} = 1$ D、 ${(x - 1)}^{2} = 1$

查看试题解析
4. 对于抛物线 $y = {(x - 1)}^{2} - 2$ 下列说法正确的是（）

A、开口向下 B、其最大值为-2 C、顶点坐标 $(- 1 ， - 2)$ D、与x轴有交点

查看试题解析
5. 如图， $A B$ 是 $⊙ O$ 的直径，点 $C$ ， $D$ 为 $⊙ O$ 上的点．若 $∠ C A B = 20 °$ ，则 $∠ D$ 的度数为（）．

A、70° B、100° C、110° D、140°

查看试题解析
6. 将抛物线y＝2（x﹣1）²﹣3向右移动2个单位，再向下移动3个单位，得到的抛物线的解析式为（）

A、y＝2（x+1）² B、y＝2（x+1）²﹣6 C、y＝2（x﹣3）² D、y＝2（x﹣3）²﹣6

查看试题解析
7. 如图，在平面直角坐标系中， $△ A B C$ 绕某点顺时针旋转得到 $△ A^{'} B^{'} C^{'}$ ，点A、B、C的对应点分别为 $A^{'}$ 、 $B^{'}$ 、 $C^{'}$ ，则旋转中心的坐标为（）

A、 $(3 ， 4)$ B、 $(3 ， 5)$ C、 $(4 ， 4)$ D、 $(4 ， 5)$

查看试题解析
8. 已知二次函数 $y = - 4 {(x - 1)}^{2} + k$ 的图象上有三点 $A (\sqrt{2} ， y_{1})$ ， $B (- 2 ， y_{2})$ ， $C (5 ， y_{3})$ ，则 $y_{1}$ 、 $y_{2}$ 、 $y_{3}$ 的大小关系为（）

A、 $y_{1} > y_{2} > y_{3}$ B、 $y_{2} > y_{1} > y_{3}$ C、 $y_{3} > y_{1} > y_{2}$ D、 $y_{3} > y_{2} > y_{1}$

查看试题解析
9. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ，将 $△ A B C$ 绕点 $A$ 顺时针旋转 $90 °$ ，得到 $△ A D E$ ，连接 $B D$ ，若 $A C = 2 \sqrt{2}$ ， $D E = 1$ ，则线段 $B D$ 的长为（）

A、3 B、 $3 \sqrt{2}$ C、 $2 \sqrt{7}$ D、 $2 \sqrt{10}$

查看试题解析
10. 如图，在宽为20米、长为32米的矩形地面上修筑同样宽的道路(图中阴影部分) ，余下部分种植草坪，要使草坪的面积为540平方米，则设道路的宽为xm，根据题意，列方程（） .

A、 $32 \times 20 - 20 x - 30 x = 540$ B、 $32 \times 20 - 20 x - 30 x - x^{2} = 540$ C、 $(32 - x) (20 - x) = 540$ D、 $32 \times 20 - 20 x - 30 x + 2 x^{2} = 540$

查看试题解析
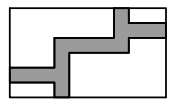11. 若函数 $y = a x^{2} + b x$ 的图象如图所示，则关于x的一元二次方程 $a x^{2} + b x + 5 = 0$ 的根的情况为（）

A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根

查看试题解析
12. 如图，正方形ABCD的边长为4，对角线AC、BD相交于点O，将△ABD绕着点B顺时针旋转45°得到△BEF，EF交CD于点G，连接BG交AC于点H，连接EH．则下列结论：①△BGE≌△BGC；②四边形EHCG是菱形；③△BDG的面积是8﹣4 $\sqrt{2}$ ；④OH＝4﹣2 $\sqrt{2}$ ．其中正确结论的序号是（）
\

A、①② B、①②③ C、①②④ D、①②③④

查看试题解析

二、填空题

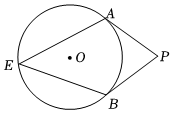
13. 方程 $x (x - 3) - 5 (x - 3) = 0$ 的根是．

查看试题解析
14. 如图，PA、PB分别切⊙O于点A，B，点E是⊙O上一点，且 $∠ E = 50 °$ ，则 $∠ P$ 的度数为．

查看试题解析
15. 如图，将 $△ A B C$ 绕点C按逆时针方向旋转至 $△ D E C$ ，使点D落在BC的延长线上．已知 $∠ A = 30 °$ ， $∠ B = 35 °$ ，则 $∠ A C E$ 的大小是．

查看试题解析
16. 如图是足球守门员在O处开出一记手抛高球后足球在空中运动到落地的过程，它是一条经过A、M、C三点的抛物线．其中A点离地面1.4米，M点是足球运动过程中的最高点，离地面3.2米，离守门员的水平距离为6米，点C是球落地时的第一点．那么足球第一次落地点C距守门员的水平距离为米．

查看试题解析
17. 如图，在扇形AOB中，AC为弦，∠AOB＝140°，∠CAO＝60°，OA＝3，则 $\overset{⌢}{B C}$ 的长为．

查看试题解析
18. 如图，已知抛物线 $y = a x^{2} + b x + c (a < 0)$ 与x轴交于 $A (x_{1} ， 0)$ ， $B (x_{2} ， 0)$ 两点，且 $- 3 < x_{1} < - 2$ ， $x_{1} + x_{2} = - 2$ ，则下列结论：① $b^{2} - 4 a c > 0$ ；②若点 $(- \frac{7}{2} ， y_{1})$ ， $(\frac{3}{4} ， y_{2})$ 是该抛物线上的点，则 $y_{1} < y_{2}$ ；③ $a t^{2} - a \leq b t - b$ （t为任意数）；④ $a + b + c < 0$ ．其中正确的有．

查看试题解析

三、解答题

19. 解方程： $x^{2} - 4 x - 5 = 0$ .

查看试题解析
20. 已知关于x的一元二次方程 $x^{2} - (2 m - 1) x + m^{2} - m = 0$ ．

(1)、求证：方程有两个不相等的实数根；

(2)、0能是方程的一个根吗？若能，求出它的另一个根；若不能，请说明理由．

查看试题解析
21. 如图，△ABC绕点O逆时针旋转90°，得到△A₁B₁C₁ ，已知 $A (- 2 ， 3)$ ， $B (- 3 ， 1)$ ， $C (- 1 ， 2)$ ．

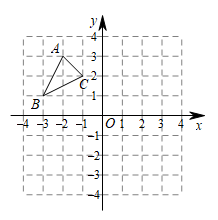(1)、画出旋转后的△A₁B₁C₁；直接写出点B₁的坐标（ ▲ ， ▲ ）；绕点O逆时针旋转90°后得到的△A₁B₁C₁；

(2)、作出△ABC关于原点O的对称图形△A₂B₂C₂ ．

查看试题解析

22. 滑雪是冬季运动爱好者的喜爱项目之一，滑雪者从山坡滑下，其滑行距离

s

（单位：

m

）是滑行时间

t

（单位：

s

）的二次函数．滑雪爱好者小聪从山坡滑下，同学小敏帮他测得一些数据，记录于下表．

滑行时间 $t / s$	0	1	2	3	4
滑行距离 $s / m$	0	4.5	14	38.5	48

(1)、在上表t，

s

的数据中，发现有一对数据记录不符合题意．在图2中，通过描点、连线的方法，画出函数的大致图象，并观察判断哪一对是错误的？

(2)、根据（1）中结果，求出

s

关于

t

的函数表达式；并求出当滑行时间为

6 s

时，小聪在山坡上滑行的距离是多少？

查看试题解析

23. 如图，在 $△ A B C$ 中， $A B = A C$ ， ⊙O是 $△ A B C$ 的外接圆，过点C作 $∠ B C D = ∠ A C B$ ，交⊙O于点D，连接AD交BC于点E，延长DC至点F，使 $C F = A C$ ，连接AF．

(1)、求证： $E D = E C$ ；

(2)、求证：AF是⊙O的切线．

查看试题解析
24. 如图，点E为正方形 $A B C D$ 外一点， $∠ A E B = 90 °$ ，将 $R t △ A B E$ 绕A点逆时针方向旋转 $90 °$ 得到 $△ A D F ， D F$ 的延长线交 $B E$ 于H点.

(1)、试判定四边形 $A F H E$ 的形状，并说明理由；

(2)、已知 $B H = 7 ， B C = 13$ ，求 $D H$ 的长.

查看试题解析
25. 在平面直角坐标系中，函数y＝x²－2ax－1（a为常数）的图象与y轴交于点A.

(1)、求点A的坐标.

(2)、当此函数图象经过点（1，2）时，求此函数的表达式，并写出函数值y随x的增大而增大时x的取值范围.

(3)、当x≤0时，若函数y＝x²－2ax－1（a为常数）的图象的最低点到直线y＝2a的距离为2，求a的值.

查看试题解析