山东省临沂市临沭县2021-2022学年九年级上学期期中数学试题

试卷更新日期：2022-09-23 类型：期中考试

进入出卷网下载

一、单选题

1. 保护环境，人人有责，下列四个图形是生活中常见的垃圾回收标志，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 方程x²=2x的根是（）

A、0 B、2 C、0或2 D、无解

查看试题解析
3. 平面直角坐标系内与点P $(- 2 ， 3)$ 关于原点对称的点的坐标是（）

A、 $(3 ， - 2)$ B、 $(2 ， 3)$ C、 $(2 ， - 3)$ D、 $(- 2 ， - 3)$

查看试题解析
4. 已知二次函数y＝a(x＋3)²－h(a≠0)有最大值1，则该函数图象的顶点坐标为（）

A、(－3，－1) B、(－3，1) C、(3，1) D、(3，－1)

查看试题解析
5. 若⊙O的半径等于10cm，圆心O到直线l的距离是6cm，则直线l与⊙O位置关系是（）

A、相交 B、相切 C、相离 D、相切或相交

查看试题解析
6. 如图，点A，B，C是 $⊙ O$ 上的三点，已知 $∠ A O B = 110 °$ ，那么 $∠ A C B$ 的度数是（）

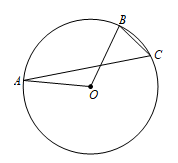A、40° B、45° C、50° D、55°

查看试题解析
7. 如图，将△AOB绕点O按逆时针方向旋转45°后得到△A＇OB＇，若∠AOB=15°，则∠AOB＇的度数是（）．

A、25° B、30° C、35° D、40°

查看试题解析
8. 如图在平面直角坐标系中，过格点A，B，C作一圆弧，圆心坐标是（）

A、 $(1 ， 0)$ B、 $(2 ， 0)$ C、 $(0 ， 0)$ D、 $(2 ， - 1)$

查看试题解析
9. 已知等腰三角形的腰和底的长分别是一元二次方程x²-7x+10=0的两个根，则该三角形的周长是（）

A、9 B、12 C、9或12 D、不能确定

查看试题解析
10. 2015年某县 $G D P$ 总量为1000亿元，计划到2017年全县 $G D P$ 总量实现1210亿元的目标，如果每年的平均增长率相同，那么该县这两年 $G D P$ 总量的年平均增长率为（）

A、 $1.21 %$ B、 $8 %$ C、 $10 %$ D、 $12.1 %$

查看试题解析
11. 已知抛物线y=x²+bx+c的部分图象如图所示，若y＞0，则x的取值范围是（）

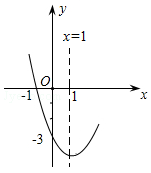A、x＜-1 B、-1＜x＜3 C、x＜-1或x＞3 D、x＜-1或x＞4

查看试题解析
12. 如图， $R t △ A B C$ 中， $∠ C = 90 °$ ， O是AB边上一点， $⊙ O$ 与AC、BC都相切，若 $B C = 3$ ， $A C = 4$ ，则 $⊙ O$ 的半径为（）

A、1 B、2 C、 $\frac{5}{2}$ D、 $\frac{12}{7}$

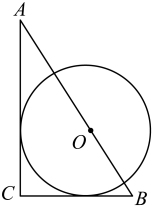查看试题解析
13. 如图所示，抛物线y=ax²+bx+c（a≠0）与x轴交于点A（-2，0）、B（1，0），直线x= $- \frac{1}{2}$ 与此抛物线交于点C，与x轴交于点M，在直线上取点D，使MD=MC，连接AC，BC，AD，BD，某同学根据图象写出下列结论：①a-b=0；②当x＜ $- \frac{1}{2}$ 时，y随x增大而增大；③四边形ACBD是菱形；④9a-3b+c＞0．你认为其中正确的是（）

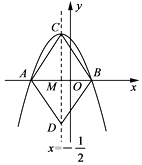A、②③④ B、①②③ C、①③④ D、①②③④

查看试题解析

二、填空题

14. 若n（n≠0）是关于x的方程x²+mx+2n=0的根，则m+n的值为.

查看试题解析
15. 如图，AB为⊙O的弦，半径OD⊥AB于点C．若AB=8，CD=2，则⊙O的半径长为．

查看试题解析
16. 正方形ABCD内一点P，AB=5，BP=2，把△ABP绕点B顺时针旋转90°得到△CBP′，则PP′的长为．

查看试题解析
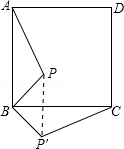17. 初三数学课本上，用“描点法”画二次函数y=ax²+bx+c的图象时，列了如下表格：
x
…
﹣2
﹣1
0
1
2
…
y
…
﹣15.5
﹣5
﹣3.5
﹣2
﹣3.5
…
根据表格上的信息回答问题：该二次函数y=ax²+bx+c在x=3时，y= ．

查看试题解析
18. 如图，P是抛物线y=2（x﹣2）²对称轴上的一个动点，直线x=t平行y轴，分别与y=x、抛物线交于点A，B．若△ABP是以点A或点B为直角顶点的等腰直角三角形，求满足条件的t的值，则t= ．

查看试题解析

三、解答题

19. 解下列方程：

(1)、 $x^{2} - 1 = 2 (x + 1)$ ；

(2)、 $2 x^{2} - 4 x - 5 = 0$ ．

查看试题解析
20. 在 $10 \times 10$ 的正方形网格中，小正方形的边长均为1个单位长度．
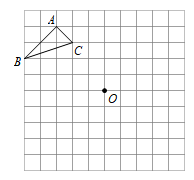
⑴画出 $△ A B C$ 绕点O逆时针旋转90°的 $△ A_{1} B_{1} C_{1}$ ；
⑵再画出 $△ A B C$ 关于点O的中心对称图形 $△ A_{2} B_{2} C_{2}$ ．

查看试题解析
21. 如下图所示，在宽为20m，长为32m的矩形耕地上，修筑同样宽的三条道路（互相垂直），把耕地分成大小不等的六块试验田，要使试验田的面积为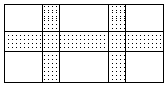 $570 m^{2}$ ，道路应为多宽？

查看试题解析
22. 某商店经营儿童益智玩具，已知成批购进时的单价是20元．调查发现：销售单价是30元时，月销售量是230件，而销售单价每上涨1元，月销售量就减少10件，但每件玩具售价不能高于40元．设每件玩具的销售单价上涨了x元时（x为正整数），月销售利润为y元．

(1)、求y与x的函数关系式并直接写出自变量x的取值范围．

(2)、每件玩具的售价定为多少元时，月销售利润恰为2520元？

(3)、每件玩具的售价定为多少元时可使月销售利润最大？最大的月利润是多少？

查看试题解析
23. 如图，AB是⊙O的直径，点F，C是⊙O上两点，且 $\overset{⌢}{A F} = \overset{⌢}{F C} = \overset{⌢}{C B}$ ，连接AC，AF，过点C作CD⊥AF交AF延长线于点D，垂足为D．

(1)、求证：CD是⊙O的切线；

(2)、若CD＝ $2 \sqrt{3}$ ，求⊙O的半径．

查看试题解析
24. 如图，已知抛物线y=x²+bx+c经过A（-1，0）、B（3，0）两点，点C是抛物线与y轴的交点．

(1)、求抛物线的解析式和顶点坐标；

(2)、当0＜x＜3时，求y的取值范围；

(3)、在抛物线的对称轴上是否存在点M，使△BCM是等腰三角形，若存在请直接写出点M坐标，若不存在请说明理由．

查看试题解析
25. 如图：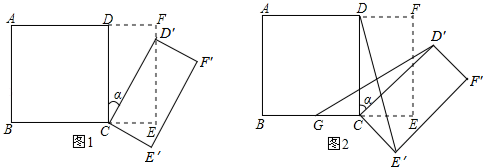
如图1所示，将一个边长为2的正方形ABCD和一个长为2、宽为1的矩形CEFD拼在一起，构成一个大的矩形ABEF．现将小矩形CEFD绕点C顺时针旋转至CE′F′D′，旋转角为α．

(1)、当点D′恰好落在EF边上时，旋转角α＝°；

(2)、如图2，G为BC中点，且0°＜α＜90°，求证：GD′＝DE′；

(3)、小矩形CEFD绕点C顺时针旋转一周的过程中，△DCD′与△CBD′能否全等？若能，直接写出旋转角α的值，若不能，说明理由．

查看试题解析

x	…	﹣2	﹣1	0	1	2	…
y	…	﹣15.5	﹣5	﹣3.5	﹣2	﹣3.5	…