山东省聊城市临清市2021-2022学年九年级上学期期中数学试题
试卷更新日期:2022-09-23 类型:期中考试
一、单选题
-
1. 的值为( )A、 B、 C、 D、2. 如图,直线 ,直线 和 被 , , 所截,如果 , , ,那么 的长是( )
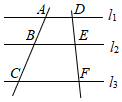 A、 B、 C、 D、3. 如图,在 的正方形网格中,每个小正方形的边长都是1, 的顶点都在这些小正方形的顶点上,那么 的值为( ).
A、 B、 C、 D、3. 如图,在 的正方形网格中,每个小正方形的边长都是1, 的顶点都在这些小正方形的顶点上,那么 的值为( ). A、 B、 C、 D、4. 如图,在▱ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( )
A、 B、 C、 D、4. 如图,在▱ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( )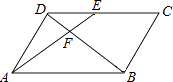 A、2:5 B、2:3 C、3:5 D、3:25. 如图,河坝横断面迎水坡的坡比为: , 坝高m,则的长度为( )
A、2:5 B、2:3 C、3:5 D、3:25. 如图,河坝横断面迎水坡的坡比为: , 坝高m,则的长度为( )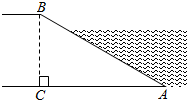 A、6m B、m C、9m D、m6. 如图,⊙O的直径CD垂直弦AB于点E,且CE=2,OB=4,则AB的长为( )
A、6m B、m C、9m D、m6. 如图,⊙O的直径CD垂直弦AB于点E,且CE=2,OB=4,则AB的长为( ) A、2 B、4 C、6 D、47. 如图,AB为⊙O的直径,∠BED=20°,则∠ACD的度数为( )
A、2 B、4 C、6 D、47. 如图,AB为⊙O的直径,∠BED=20°,则∠ACD的度数为( ) A、80° B、75° C、70° D、65°8. 如图所示,在平面直角坐标系中,已知点A(2,4),过点A作AB⊥x轴于点B.将△AOB以坐标原点O为位似中心缩小为原图形的 ,得到△COD,则CD的长度是( )
A、80° B、75° C、70° D、65°8. 如图所示,在平面直角坐标系中,已知点A(2,4),过点A作AB⊥x轴于点B.将△AOB以坐标原点O为位似中心缩小为原图形的 ,得到△COD,则CD的长度是( ) A、1 B、2 C、2 D、9. 正三角形内切圆与外接圆半径之比为( )A、 B、 C、 D、10. 如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与 相似的是( )
A、1 B、2 C、2 D、9. 正三角形内切圆与外接圆半径之比为( )A、 B、 C、 D、10. 如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与 相似的是( ) A、
A、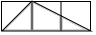 B、
B、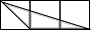 C、
C、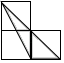 D、
D、 11. 如图,在平面直角坐标系中,O为坐标原点,为 , 点A的坐标是 , , 把绕点A按顺时针方向旋转后,得到 , 则的外接圆圆心坐标是( )
11. 如图,在平面直角坐标系中,O为坐标原点,为 , 点A的坐标是 , , 把绕点A按顺时针方向旋转后,得到 , 则的外接圆圆心坐标是( ) A、 B、 C、 D、12. 2020年平阴街道进行拓宽改造,县城面貌焕然一新,拓宽后振兴街主路双向四车道16米宽,两边安装路灯,如图路灯的灯臂 长2米,且与灯柱 成 角,路灯采用圆锥形灯罩,灯罩的轴线 与灯臂 垂直,当灯罩的轴线 通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱 高度应该设计为( )
A、 B、 C、 D、12. 2020年平阴街道进行拓宽改造,县城面貌焕然一新,拓宽后振兴街主路双向四车道16米宽,两边安装路灯,如图路灯的灯臂 长2米,且与灯柱 成 角,路灯采用圆锥形灯罩,灯罩的轴线 与灯臂 垂直,当灯罩的轴线 通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱 高度应该设计为( ) A、6米 B、 米 C、 米 D、 米
A、6米 B、 米 C、 米 D、 米二、填空题
-
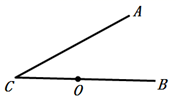
13. 在中, , , , 那么AB的长为 .14. 如图, ,点 是 上的一点,且 ,则以4为半径的 与直线 的公共点的个数 .
 15. 如图,P是⊙O外一点,过P引⊙O的切线PA、PB,若∠APB=50°,则的度数为 .
15. 如图,P是⊙O外一点,过P引⊙O的切线PA、PB,若∠APB=50°,则的度数为 .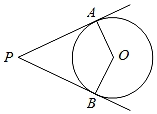 16. 如图,小华同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,使斜边DF与地面保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边 , ,测得边DF离地面的高度 , ,则树AB的高度为cm.
16. 如图,小华同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,使斜边DF与地面保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边 , ,测得边DF离地面的高度 , ,则树AB的高度为cm. 17. 如图,在Rt△ABC中,∠C=90°,AC=2,BC=4.点M1 , N1 , P1分别在AC,BC,AB上,且四边形M1CN1P1是正方形,点M2 , N2 , P2分别在P1N1 , BN1 , BP1上,且四边形M2N1N2P2是正方形,…,点Mn,Nn,Pn分别在Pn﹣1Nn﹣1 , BNn﹣1 , BPn﹣1上,且四边形MnNn﹣1NnPn是正方形,则线段MnPn的长度是 .
17. 如图,在Rt△ABC中,∠C=90°,AC=2,BC=4.点M1 , N1 , P1分别在AC,BC,AB上,且四边形M1CN1P1是正方形,点M2 , N2 , P2分别在P1N1 , BN1 , BP1上,且四边形M2N1N2P2是正方形,…,点Mn,Nn,Pn分别在Pn﹣1Nn﹣1 , BNn﹣1 , BPn﹣1上,且四边形MnNn﹣1NnPn是正方形,则线段MnPn的长度是 .
三、解答题
-
18. 计算:(1)、2sin30°+4cos30°⋅tan60°﹣cos245°;(2)、sin230°+cos230°+cos60°tan45°.19. 如图,已知点O是坐标原点,B、C两点的坐标分别为(3,-1),(2,1).
 (1)、以O点为位似中心在y轴的左侧将△OBC放大到原图的2倍(即新图与原图的相似比为2),画出对应的△OBꞌCꞌ;(2)、若△OBC内部一点M的坐标为(a,b),则点M对应点M′的坐标是;(3)、求出变化后△OBꞌCꞌ的面积.20. 如图,在⊙O中,ACOB,∠BAO=25°,求∠BOC的度数.
(1)、以O点为位似中心在y轴的左侧将△OBC放大到原图的2倍(即新图与原图的相似比为2),画出对应的△OBꞌCꞌ;(2)、若△OBC内部一点M的坐标为(a,b),则点M对应点M′的坐标是;(3)、求出变化后△OBꞌCꞌ的面积.20. 如图,在⊙O中,ACOB,∠BAO=25°,求∠BOC的度数. 21. 如图,在矩形中,点是的中点,交于点.
21. 如图,在矩形中,点是的中点,交于点. (1)、求证:;(2)、若 , , 求的长.22. 在△ABC中,∠B=45°,∠C=30°,若AB=2 ,求AC的长.
(1)、求证:;(2)、若 , , 求的长.22. 在△ABC中,∠B=45°,∠C=30°,若AB=2 ,求AC的长. 23. 某区域平面示意图如图,点O在河的一侧,AC和BC表示两条互相垂直的公路.甲勘测员在A处测得点O位于北偏东45°,乙勘测员在B处测得点O位于南偏西73.7°,测得AC=840m,BC=500m.请求出点O到公路AC的距离.(参考数据:sin73.7°≈ , cos73.7°≈ , tan73.7°≈)
23. 某区域平面示意图如图,点O在河的一侧,AC和BC表示两条互相垂直的公路.甲勘测员在A处测得点O位于北偏东45°,乙勘测员在B处测得点O位于南偏西73.7°,测得AC=840m,BC=500m.请求出点O到公路AC的距离.(参考数据:sin73.7°≈ , cos73.7°≈ , tan73.7°≈) 24. 如图,AB是⊙O的直径,弦AD平分∠BAC,过点D作DE⊥AC于E.
24. 如图,AB是⊙O的直径,弦AD平分∠BAC,过点D作DE⊥AC于E. (1)、求证:ED是⊙O的切线;(2)、若ED,AB的延长线相交于F,且AE=5,EF=12,求⊙O的半径.25. 顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角.如图①所示:PA切⊙O于点A,AB是⊙O的一条弦,∠PAB就是⊙O的一个弦切角.经研究发现:弦切角等于它夹弧所对的圆周角.根据下面的“已知”和“求证”,写出“证明”过程,并回答后面的问题.
(1)、求证:ED是⊙O的切线;(2)、若ED,AB的延长线相交于F,且AE=5,EF=12,求⊙O的半径.25. 顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角.如图①所示:PA切⊙O于点A,AB是⊙O的一条弦,∠PAB就是⊙O的一个弦切角.经研究发现:弦切角等于它夹弧所对的圆周角.根据下面的“已知”和“求证”,写出“证明”过程,并回答后面的问题. (1)、如图1,PA是⊙O的切线,A为切点,AC为直径,∠PAB夹弧所对的圆周角为∠C.求证:∠PAB=∠C.(2)、如图2,PA是⊙O的切线,A为切点,∠PAB夹弧所对的圆周角为∠D.求证:∠PAB=∠D.(3)、如图3,AB为半⊙O的直径,O为圆心,C,D为半⊙O上两点,过点C作半⊙O的切线CE交AD的延长线于点E,若CE⊥AD,且BC=1,AB=3,求DE的长.
(1)、如图1,PA是⊙O的切线,A为切点,AC为直径,∠PAB夹弧所对的圆周角为∠C.求证:∠PAB=∠C.(2)、如图2,PA是⊙O的切线,A为切点,∠PAB夹弧所对的圆周角为∠D.求证:∠PAB=∠D.(3)、如图3,AB为半⊙O的直径,O为圆心,C,D为半⊙O上两点,过点C作半⊙O的切线CE交AD的延长线于点E,若CE⊥AD,且BC=1,AB=3,求DE的长.