山东省济宁市泗水县2021-2022学年九年级上学期期中数学试题

试卷更新日期：2022-09-23 类型：期中考试

进入出卷网下载

一、单选题

1. 下列慈善公益图标中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 方程kx²+3x＝x²+5是关于x的一元二次方程，则k的取值范围是（）

A、k≠0 B、k≠﹣1 C、k≠1 D、k≠±1

查看试题解析
3. 如图，AB是⊙O的直径．若∠BAC＝43°，那么∠ABC的度数是（）

A、43° B、47° C、53° D、57°

查看试题解析
4. 在平面直坐标系中，将抛物线y＝x²﹣4先向左平移2个单位，再向上平移3个单位，得到的抛物线的解析式是（）

A、y＝（x+2）²+11 B、y＝（x﹣2）²﹣1 C、y＝（x﹣2）²+1 D、y＝（x+2）²﹣1

查看试题解析
5. 小明不慎把家里的圆形镜子打碎了，其中三块碎片如图所示，三块碎片中最有可能配到与原来一样大小的圆形镜子的碎片是（）

A、① B、② C、③ D、均不可能

查看试题解析
6. 如图，平面直角坐标系xOy中，点A．B，C．D都在边长为1的小正方形网格的格点上，过点M（1，﹣2）的抛物线y＝mx²+2mx+n（m＞0）可能还经过（）

A、点A B、点B C、点C D、点D

查看试题解析
7. 某广场有一块正方形的空地正中间修建一个圆形喷泉，在四个角修建四个四分之一圆形的水池，其余部分种植花草，若喷泉和水池的半径都相同，喷泉边缘到空地边界的距离为3m，种植花草的区域的面积为100m，设水池半径为xm，可列出方程（）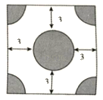

A、（2x+3）²﹣πx²＝100 B、（x+6）²﹣πx²＝100 C、（2x+3）²﹣2x²＝100 D、（2x+6）²﹣2πx²＝100

查看试题解析
8. 如图，在等腰△ABC中，AB＝AC＝4 $\sqrt{5}$ ， BC＝16，按下列步骤作图：①以点A为圆心，适当的长度为半径作弧，分别交AB，AC于点E，F，再分别以点E，F为圆心，大于 $\frac{1}{2}$ EF的长为半径作弧相交于点H，作射线AH；②分别以点A，B为圆心，大于 $\frac{1}{2}$ AB的长为半径作弧相交于点M，N，作直线MN，交射线AH于点O；③以点O为圆心，线段OA长为半径作圆．则⊙O的半径为（）

A、4 $\sqrt{5}$ B、10 C、5 D、4

查看试题解析
9. 如图，点E是正方形ABCD的边DC上一点，把△ADE绕点A顺时针旋转90°到△ABF的位置，若四边形AECF的面积为144．AE＝13．则DE的长为（）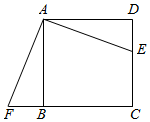

A、2 $\sqrt{3}$ B、 $\sqrt{13}$ C、4 D、5

查看试题解析
10. 如图，抛物线y＝ax²+bx+c（a≠0）与x轴交于点A、B．顶点为C．对称轴为直线x＝1．给出下列结论：①abc＜0；②4ac﹣b²＜0；③m（am+b）﹣b＜a；④若点A的坐标为（﹣2，0），则3a+c＜0；⑤若点B的坐标为（4，0），当y＞0时，﹣2＜x＜4；⑥若M（x₁ ， y₁），N（x₁ ， x₂）是抛物线上两点（1＜x₁＜x₂），则y₁＞y₂；⑦若抛物线经过点（1，3），方程ax²+bx+cm＝0没有实数根，则m＜3．其中正确结论的个数为（）

A、3 B、4 C、5 D、6

查看试题解析

二、填空题

11. 已知x＝1是方程x²+bx﹣5＝0的一个根，则方程的另一个根是．

查看试题解析
12. 点A（﹣2，﹣1）绕点B（﹣1，0）旋转180°得到点C．则点C坐标为．

查看试题解析
13. 如图，AB为⊙O直径，BC＝4，AC＝3，CD平分∠ACB，则AD＝．

查看试题解析
14. 如图，将Rt△ABC的斜边AB与量角器的直径恰好重合，B点与零刻度线的一端重合，∠ABC＝38°，射线CD绕点C转动，与量角器外沿交于点D，若射线CD将△ABC分割出以BC为边的等腰三角形，则点D在量角器上对应的度数是．

查看试题解析
15. 如图，一段抛物线：y＝﹣x（x﹣2）（0≤x≤2）记为C₁ ，它与x轴交于两点O、A₁；将C₁绕A₁能转180°得到C₂ ，交x轴于A₂；将C₂绕A₂旋转180°得到C₃ ，交x轴于A₃.此进行下去，直至得到C₂₀₂₁ ，若顶点P（m，n）在第2021段抛物线C₂₀₂₁上，则m＝．

查看试题解析

三、解答题

16. 解下列方程：

(1)、x²﹣3x﹣10＝0．

(2)、（x﹣3）²+2x（x﹣3）＝0．

查看试题解析
17. 如图，△ABC三个顶点的坐标分别为A（1，1），B（4.2）．C（3.4）
⑴请画出将△ABC向左平移6个单位长度后得到的图形△A₁B₁C₁；
⑵请画出△ABC绕原点O顺时针旋转90°的图形△A₂B₂C₂；
⑶△A₂B₂C₂可看成将△A₁B₁C₁以某点为旋转中心旋转而得，则旋转中心的坐标是 ▲ ．

查看试题解析
18. 已知关于x的一元次方程x²+mx+m﹣3＝0．

(1)、求证：无论m取任何实数，方程总有两个不相等的实数根；

(2)、设x²+mx+m﹣3＝0的两个实数根为x₁ ， x₂ ，若y＝x₁²+x₂²+4x₁x₂.求y与m的函数解析式．

查看试题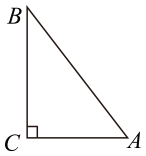解析
19. 如图：

(1)、实践操作：如图，△ABC是直角三角形，∠ACB＝90°，利用直尺和圆规按下列要求作图，并在图中标明相应的字母．
（保留作图痕迹，不写作法）
①作∠BAC的平分线，交BC于点O．
②以O为圆心，OC为半径作圆．

(2)、综合运用：在你所作的图中，直线AB与⊙O存在怎样的位置关系，请说明理由．

(3)、若AC＝6，BC＝8，则⊙O的半径为．

查看试题解析
20. 某商店以每件80元的价格购进一批商品，现以单价100元销售，每月可售出300件．经市场调查发现：每件商品销售单价每上涨1元，该商品平均每月的销售量就减少10件，设每件商品销售单价上涨了x元．

(1)、若在顾客得实惠的前提下，当每件商品销售单价上涨多少元时，该商店每月的销售利润为6210元？

(2)、写出月销售该商品的利润y（元）与每件商品销售单价上涨x（元）之间的函数关系式；当销售单价定为多少元时，每月销售该商品的利润最大？最大利润为多少？

查看试题解析
21. 如图：

如图1，在 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 60 °$ ， D为BC边上一点（不与点B，C重合）．将线段AD绕点A逆时针旋转60°得到AE，连接EC，则：

(1)、① $∠ A C E$ 的度数是；
②线段AC，CD，CE之间的数量关系是．

(2)、如图2，在 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 90 °$ ， D为BC边上一点（不与点B，C重合），将线段AD绕点A逆时针旋转90°得到AE，连接EC，请写出 $∠ A C E$ 的度数及线段AD，BD，CD之间的数量关系，并说明理由；

(3)、如图3，在 $R t △ D B C$ 中， $D B = 3$ ， $D C = 5$ ， $∠ B D C = 90 °$ ，若点 $A$ 满足 $A B = A C$ ， $∠ B A C = 90 °$ ，请直接写出线段AD的长度．

查看试题解析
22. 如图，抛物线y＝ax²+bx﹣4a（a≠0）经过A（﹣1，0），C（0，4）两点，与x轴交于另一点B，连接AC，BC．

(1)、求抛物线的解析式；

(2)、平行于x轴的直线y＝﹣14与抛物线分别交于点D、E，求线段DE的长．

(3)、点P是线段OB上一点（不与点B、O重合），过点P作PM⊥x轴交抛物线于点M，连接CM、BM，求△BCM面积的最大值，及此时点M坐标．

查看试题解析