山东省济南市历下区2021-2022学年九年级上学期期中数学试题
试卷更新日期:2022-09-23 类型:期中考试
一、单选题
-
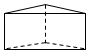
1. 一个几何体如图水平放置,它的主视图是( )
 A、
A、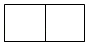 B、
B、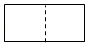 C、
C、 D、
D、 2. 下列各点中,在反比例函数 图象上的是( )A、(2,4) B、(﹣1,8) C、(2,﹣4) D、(﹣16,﹣2)3. 以下列数据(单位:cm)为长度的各组线段中,成比例线段的是( )A、1,2,3,4 B、3,6,9,18 C、1,2,2,6 D、1, , 4,34. 如图,两条直线被三条平行线所截,若AC=4,CE=6,BD=2,则DF=( )
2. 下列各点中,在反比例函数 图象上的是( )A、(2,4) B、(﹣1,8) C、(2,﹣4) D、(﹣16,﹣2)3. 以下列数据(单位:cm)为长度的各组线段中,成比例线段的是( )A、1,2,3,4 B、3,6,9,18 C、1,2,2,6 D、1, , 4,34. 如图,两条直线被三条平行线所截,若AC=4,CE=6,BD=2,则DF=( )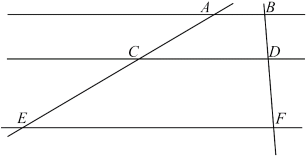 A、1 B、2 C、3 D、45. 某小组在“用频率估计概率”的实验中,统计了某种频率结果出现的频率,绘制了如图所示的折线统计图,那么符合这一结果的实验最有可能的是( )
A、1 B、2 C、3 D、45. 某小组在“用频率估计概率”的实验中,统计了某种频率结果出现的频率,绘制了如图所示的折线统计图,那么符合这一结果的实验最有可能的是( ) A、掷一枚质地均匀的硬币,落地时结果是“正面向上” B、掷一个质地均匀的正六面体骰子,落地时朝上的面点数是6 C、在“石头剪刀、和”的游戏中,小明随机出的是“剪刀” D、袋子中有1个红球和2个黄球,只有颜色上的区别,从中随机取出一个球是黄球6. 在如图所示的三个矩形中,相似的是( )
A、掷一枚质地均匀的硬币,落地时结果是“正面向上” B、掷一个质地均匀的正六面体骰子,落地时朝上的面点数是6 C、在“石头剪刀、和”的游戏中,小明随机出的是“剪刀” D、袋子中有1个红球和2个黄球,只有颜色上的区别,从中随机取出一个球是黄球6. 在如图所示的三个矩形中,相似的是( ) A、甲和乙 B、甲和丙 C、乙和丙 D、甲、乙和丙7. 如图,D、E分别是△ABC边AB、AC上的点,DE∥BC,且AD:BD=1:2,那么S△ADE:S△ABC的值为( )
A、甲和乙 B、甲和丙 C、乙和丙 D、甲、乙和丙7. 如图,D、E分别是△ABC边AB、AC上的点,DE∥BC,且AD:BD=1:2,那么S△ADE:S△ABC的值为( ) A、1:4 B、1:6 C、1:8 D、1:98. 若点A(﹣2,y1),B(2,y2),C(3,y3)都在反比例函数的图象上,则y1 , y2 , y3的大小关系是( )A、y2<y3<y1 B、y3<y2<y1 C、y3<y1<y2 D、y1<y2<y39. 若点C是线段AB的黄金分割点,且AB=2(AC>BC),则AC等于( )A、 ﹣1 B、3﹣ C、 D、 ﹣1或3﹣10. 在同一平面直角坐标系中,函数和的图象大致是( )A、
A、1:4 B、1:6 C、1:8 D、1:98. 若点A(﹣2,y1),B(2,y2),C(3,y3)都在反比例函数的图象上,则y1 , y2 , y3的大小关系是( )A、y2<y3<y1 B、y3<y2<y1 C、y3<y1<y2 D、y1<y2<y39. 若点C是线段AB的黄金分割点,且AB=2(AC>BC),则AC等于( )A、 ﹣1 B、3﹣ C、 D、 ﹣1或3﹣10. 在同一平面直角坐标系中,函数和的图象大致是( )A、 B、
B、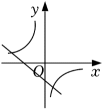 C、
C、 D、
D、 11. 直角三角形中, , 三个正方形如图放置,边长分别为 , , , 已知 , , 则的值为( )
11. 直角三角形中, , 三个正方形如图放置,边长分别为 , , , 已知 , , 则的值为( )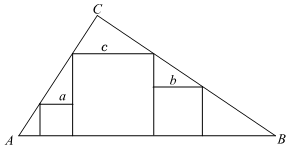 A、4 B、 C、5 D、612. 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点EF,连接BD、DP,BD与CF相交于点H.给出下列结论:①AE=FC;②∠PDE=15°;③;④DE2=PF•FC.其中正确的为( )
A、4 B、 C、5 D、612. 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点EF,连接BD、DP,BD与CF相交于点H.给出下列结论:①AE=FC;②∠PDE=15°;③;④DE2=PF•FC.其中正确的为( ) A、①②③ B、①③ C、②③④ D、①②④
A、①②③ B、①③ C、②③④ D、①②④二、填空题
-
13. 若点A(1,﹣3),B(m+1,3)在同一反比例函数的图象上,则m的值为 .14. 一个不透明的口袋中放着若干个红球和白球,这两种球除了颜色以外没有任何其它区别,袋中的球已经搅匀,从口袋中随机取出一个球,取出红球的概率是 . 如果袋中共有32个小球,那么袋中的红球的个数为 个.15. 如图,已知路灯离地面的高度AB为4.8m,身高为1.6m的小明站在D处的影长为2m,那么此时小明离电杆AB的距离BD为m.
 16. 如在平面直角坐标系中,等腰直角△ABO如图放置,直角顶点A在反比例函数的图形上,其中AB=AO,B(-2,0),则k= .
16. 如在平面直角坐标系中,等腰直角△ABO如图放置,直角顶点A在反比例函数的图形上,其中AB=AO,B(-2,0),则k= . 17. 如图,在矩形ABCD中,E是BC的中点,连接AE,过点E作EF⊥AE交DC于点F.若AB=4,BC=6,则DF的长为 .
17. 如图,在矩形ABCD中,E是BC的中点,连接AE,过点E作EF⊥AE交DC于点F.若AB=4,BC=6,则DF的长为 . 18. 将一副三角板如图放置在平面直角坐标系中,直角顶点A在y轴的正半轴上,CB⊥x轴于点B,OB=6,点E、F分别是AC、CD的中点,将这副三角板整体向右平移 个单位,E,F两点同时落在反比例函数的图象上.
18. 将一副三角板如图放置在平面直角坐标系中,直角顶点A在y轴的正半轴上,CB⊥x轴于点B,OB=6,点E、F分别是AC、CD的中点,将这副三角板整体向右平移 个单位,E,F两点同时落在反比例函数的图象上.
三、解答题
-
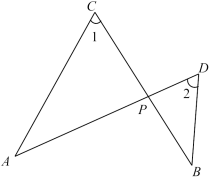
19. 已知 , 且2x+3y﹣z=18,求x+y+z的值.20. 如图,AD、BC相交于点P,连接AC、BD,且∠1=∠2,AC=3,CP=2,DP=1,求BD的长.
 21. 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2)
21. 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2)
⑴画出△ABC关于点B成中心对称的图形△A1BC1;
⑵以原点O为位似中心,位似比为1:2,在y轴的左侧画出△ABC放大后的图形△A2B2C2 , 并直接写出C2的坐标.
22. 为了测量水平地面上一栋建筑物AB的高度,学校数学兴趣小组做了如下的探索:根据光的反射定律,利用一面镜子和一根皮尺,设计如图所示的测量方案:先在水平地面上放置一面平面镜,并在镜面上做标记点C,后退至点D处恰好看到建筑物AB的顶端A在镜子中的像与镜面上的标记点C重合,法线是FC,小军的眼睛与地面距离DE是1.65m,BC、CD的长分别为60m、3m,求建筑物AB的高度. 23. 为了迎接建党100周年,学校举办了“感党恩•跟党走”主题社团活动,小颖喜欢的社团有写作社团、书画社团、演讲社团、舞蹈社团(分别用字母A , B , C , D依次表示这四个社团),并把这四个字母分别写在四张完全相同的不透明的卡片正面,然后将这四张卡片背面朝上洗匀后放在桌面上.(1)、小颖从中随机抽取一张卡片是舞蹈社团D的概率是;(2)、小颖先从中随机抽取一张卡片,记录下卡片上的字母不放回,再从剩下的卡片中随机抽取一张卡片,记录下卡片上的字母,请用列表法或画树状图法求出小颖抽取的两张卡片中有一张是演讲社团C的概率.24. 学生上课时注意力集中的程度可以用注意力指数表示.某班学生在一节数学课中的注意力指数y随上课时间x(分钟)的变化图象如图.上课开始时注意力指数为30,第2分钟时注意力指数为40,前10分钟内注意力指数y是时间x的一次函数.10分钟以后注意力指数y是x的反比例函数.
23. 为了迎接建党100周年,学校举办了“感党恩•跟党走”主题社团活动,小颖喜欢的社团有写作社团、书画社团、演讲社团、舞蹈社团(分别用字母A , B , C , D依次表示这四个社团),并把这四个字母分别写在四张完全相同的不透明的卡片正面,然后将这四张卡片背面朝上洗匀后放在桌面上.(1)、小颖从中随机抽取一张卡片是舞蹈社团D的概率是;(2)、小颖先从中随机抽取一张卡片,记录下卡片上的字母不放回,再从剩下的卡片中随机抽取一张卡片,记录下卡片上的字母,请用列表法或画树状图法求出小颖抽取的两张卡片中有一张是演讲社团C的概率.24. 学生上课时注意力集中的程度可以用注意力指数表示.某班学生在一节数学课中的注意力指数y随上课时间x(分钟)的变化图象如图.上课开始时注意力指数为30,第2分钟时注意力指数为40,前10分钟内注意力指数y是时间x的一次函数.10分钟以后注意力指数y是x的反比例函数. (1)、当0≤x≤10时,求y关于x的函数关系式;(2)、当10≤x≤40时,求y关于x的函数关系式;(3)、如果讲解一道较难的数学题要求学生的注意力指数不小于50,为了保证教学效果本节课讲完这道题不能超过多少分钟?25. 如图所示,在矩形ABCD中,AB=12cm,BC=6cm.点P沿AB边从点A开始向点B以2cm/秒的速度移动,点Q沿DA边从点D开始向点A以1cm/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6),那么:
(1)、当0≤x≤10时,求y关于x的函数关系式;(2)、当10≤x≤40时,求y关于x的函数关系式;(3)、如果讲解一道较难的数学题要求学生的注意力指数不小于50,为了保证教学效果本节课讲完这道题不能超过多少分钟?25. 如图所示,在矩形ABCD中,AB=12cm,BC=6cm.点P沿AB边从点A开始向点B以2cm/秒的速度移动,点Q沿DA边从点D开始向点A以1cm/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6),那么: (1)、点Q运动多少秒时,△APQ的面积为5cm2;(2)、当t为何值时,△QAP与△ABC相似?26. 已知,矩形OCBA在平面直角坐标系中的位置如图所示,点C在x轴的正半轴上,点A在y轴的正半轴上,已知点B的坐标为(4,2),反比例函数的图象经过AB的中点D,且与BC交于点E,设直线DE的解析式为y=mx+n,连接OD,OE.
(1)、点Q运动多少秒时,△APQ的面积为5cm2;(2)、当t为何值时,△QAP与△ABC相似?26. 已知,矩形OCBA在平面直角坐标系中的位置如图所示,点C在x轴的正半轴上,点A在y轴的正半轴上,已知点B的坐标为(4,2),反比例函数的图象经过AB的中点D,且与BC交于点E,设直线DE的解析式为y=mx+n,连接OD,OE. (1)、求反比例函数的表达式和点E的坐标;(2)、直接写出不等式>mx+n的解集;(3)、点M为y轴正半轴上一点,若△MBO的面积等于△ODE的面积,求点M的坐标;(4)、点P为x轴上一点,点Q为反比例函数图象上一点,是否存在点P、Q使得以点P,Q,D,E为顶点的四边形为平行四边形?若存在,直接写出点Q的坐标;若不存在,请说明理由.27. 在△ABC中,∠ACB=90°,∠BAC=60°,点D在斜边AB上,且满足BD=AB,将线段DB绕点D逆时针旋转至DE,记旋转角为α,连接AE,BE,以AE为斜边在其一侧作直角三角形AEF,且∠AFE=90°,∠EAF=60°,连接CF.
(1)、求反比例函数的表达式和点E的坐标;(2)、直接写出不等式>mx+n的解集;(3)、点M为y轴正半轴上一点,若△MBO的面积等于△ODE的面积,求点M的坐标;(4)、点P为x轴上一点,点Q为反比例函数图象上一点,是否存在点P、Q使得以点P,Q,D,E为顶点的四边形为平行四边形?若存在,直接写出点Q的坐标;若不存在,请说明理由.27. 在△ABC中,∠ACB=90°,∠BAC=60°,点D在斜边AB上,且满足BD=AB,将线段DB绕点D逆时针旋转至DE,记旋转角为α,连接AE,BE,以AE为斜边在其一侧作直角三角形AEF,且∠AFE=90°,∠EAF=60°,连接CF. (1)、如图1,当α=180°时,请直接写出线段BE与线段CF的数量关系;(2)、当0°<α<180°时,
(1)、如图1,当α=180°时,请直接写出线段BE与线段CF的数量关系;(2)、当0°<α<180°时,①如图2,(1)中线段BE与线段CF的数量关系是否仍然成立?诸说明理由;
②如图3,当B,E,F三点共线时,连接CE,判断△CEF的形状,并证明.