山东省济南市济阳区2021-2022学年九年级上学期期中考试数学试题
试卷更新日期:2022-09-23 类型:期中考试
一、单选题
-
1. 下列关于 的方程是一元二次方程的是( ).A、 B、 C、 D、2. 下列命题是真命题的是( )A、对角线相等的四边形是平行四边形 B、对角线互相平分且相等的四边形是矩形 C、对角线互相垂直的四边形是菱形 D、对角线互相垂直平分的四边形是正方形3. 用配方法解方程 ,配方后所得的方程是( )A、 B、 C、 D、4. 在一个不透明的盒子中,装有除颜色外完全相同的乒乓球共16个,从中随机摸出一个乒乓球,若摸到黄色乒乓球的概率为 , 则该盒子中装有黄色乒乓球的个数是( ).A、5个 B、6个 C、7个 D、8个5. 如图,身高为1.5米的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3米,CA=1米,则树的高度为( )
 A、4.5米 B、6米 C、3米 D、4米6. 线段AB的长是10,点C是AB的黄金分割点,且AC>BC,则AC的长为( )A、5﹣ B、 C、15﹣3 D、5 ﹣57. 如图,在菱形 中, 是 的中点, ,交 于点 ,如果 ,那么菱形 的周长是( )
A、4.5米 B、6米 C、3米 D、4米6. 线段AB的长是10,点C是AB的黄金分割点,且AC>BC,则AC的长为( )A、5﹣ B、 C、15﹣3 D、5 ﹣57. 如图,在菱形 中, 是 的中点, ,交 于点 ,如果 ,那么菱形 的周长是( )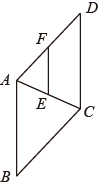 A、11 B、22 C、33 D、448. 朝阳文具店二月销售签字笔40支,三月、四月销售量连续增长,四月销售量为90支,求月平均增长率.设月平均增长率为x,根据题意可列方程为( )A、40(1+x2)=90 B、40(1+2x)=90 C、40(1+x)2=90 D、90(1-x)2=409. 如图,平行于BC的直线DE把△ABC分成面积相等的两部分,则 的值为( )
A、11 B、22 C、33 D、448. 朝阳文具店二月销售签字笔40支,三月、四月销售量连续增长,四月销售量为90支,求月平均增长率.设月平均增长率为x,根据题意可列方程为( )A、40(1+x2)=90 B、40(1+2x)=90 C、40(1+x)2=90 D、90(1-x)2=409. 如图,平行于BC的直线DE把△ABC分成面积相等的两部分,则 的值为( ) A、1 B、 C、 -1 D、 +110. 某小组在“用频率估计概率”的实验中,统计了某种频率结果出现的频率,绘制了如图所示的折线统计图,那么符合这一结果的实验最有可能的是( )
A、1 B、 C、 -1 D、 +110. 某小组在“用频率估计概率”的实验中,统计了某种频率结果出现的频率,绘制了如图所示的折线统计图,那么符合这一结果的实验最有可能的是( ) A、掷一枚质地均匀的硬币,落地时结果是“正面向上” B、掷一个质地均匀的正六面体骰子,落地时朝上的面点数是6 C、在“石头剪刀、和”的游戏中,小明随机出的是“剪刀” D、袋子中有1个红球和2个黄球,只有颜色上的区别,从中随机取出一个球是黄球11.
A、掷一枚质地均匀的硬币,落地时结果是“正面向上” B、掷一个质地均匀的正六面体骰子,落地时朝上的面点数是6 C、在“石头剪刀、和”的游戏中,小明随机出的是“剪刀” D、袋子中有1个红球和2个黄球,只有颜色上的区别,从中随机取出一个球是黄球11.如图,矩形ABCD中,AB=3,BC=5.过对角线交点O作OE⊥AC交AD于E,则AE的长是( )
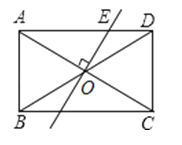 A、1.6 B、2.5 C、3 D、3.412. 如图,在中, , , 点、分别在、上, , , 交于点 , 则面积的最大值是( )
A、1.6 B、2.5 C、3 D、3.412. 如图,在中, , , 点、分别在、上, , , 交于点 , 则面积的最大值是( ) A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
13. 若 = ,则 = .14. 如图,在两个同心圆中,四条直径把大圆分成八等份,若往圆面投掷飞镖,则飞镖落在黑色区域的概率是.
 15. 已知关于x的一元二次方程有一个根为1,则k的值是 .16. 如图,△OAB和△OCD位似,位似中心是原点O,B点坐标是(6,2),△OAB和△OCD的相似比为2:1,则点D的坐标为 .
15. 已知关于x的一元二次方程有一个根为1,则k的值是 .16. 如图,△OAB和△OCD位似,位似中心是原点O,B点坐标是(6,2),△OAB和△OCD的相似比为2:1,则点D的坐标为 . 17. 如图,某小区计划在一块长为 , 宽为的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为 , 则道路宽为 .
17. 如图,某小区计划在一块长为 , 宽为的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为 , 则道路宽为 . 18. 在平面直角坐标系中,对于平面内任一点 , 若规定以下两种变换:
18. 在平面直角坐标系中,对于平面内任一点 , 若规定以下两种变换:⑴ . 如:;
⑵ . 如:;
按照以上变换有: , 那么等于 .
三、解答题
-
19. 解方程:(1)、 .(2)、20. 如图,E是正方形ABCD对角线BD上的一点,求证:AE=CE.
 21. 如图,零件的外径为16cm,要求它的壁厚x,需要先求出内径AB,现用一个交叉钳(AD与BC相等)去量,若测得OA︰OD=OB︰OC=3︰1,CD=5cm,你能求零件的壁厚x吗?
21. 如图,零件的外径为16cm,要求它的壁厚x,需要先求出内径AB,现用一个交叉钳(AD与BC相等)去量,若测得OA︰OD=OB︰OC=3︰1,CD=5cm,你能求零件的壁厚x吗? 22. 如图,在△ABC中,AB=10cm,BC=20cm,点P从点A开始沿AB边向B点以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动,如果点P、Q分别从A、B同时出发,问经过几秒钟,△PBQ与△ABC相似.
22. 如图,在△ABC中,AB=10cm,BC=20cm,点P从点A开始沿AB边向B点以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动,如果点P、Q分别从A、B同时出发,问经过几秒钟,△PBQ与△ABC相似. 23. 某商场服装部销售一种名牌衬衫,平均每天可售出30件,每件盈利40元.为了增加销量,减少库存,商场决定降价销售,经调查,每件降价1元时,平均每天可多卖出2件.(1)、若降价3元,则平均每天销售数量为件;(2)、当每件商品降价多少元时,该商店每天销售利润为1200元?24. 为庆祝中国共产党成立100周年,落实教育部《关于在中小学组织开展“从小学党史,永远跟党走”主题教育活动的通知》要求,某学校举行党史知识竞赛,随机调查了部分学生的竞赛成绩,绘制成两幅不完整的统计图表.根据统计图表提供的信息,解答下列问题:
23. 某商场服装部销售一种名牌衬衫,平均每天可售出30件,每件盈利40元.为了增加销量,减少库存,商场决定降价销售,经调查,每件降价1元时,平均每天可多卖出2件.(1)、若降价3元,则平均每天销售数量为件;(2)、当每件商品降价多少元时,该商店每天销售利润为1200元?24. 为庆祝中国共产党成立100周年,落实教育部《关于在中小学组织开展“从小学党史,永远跟党走”主题教育活动的通知》要求,某学校举行党史知识竞赛,随机调查了部分学生的竞赛成绩,绘制成两幅不完整的统计图表.根据统计图表提供的信息,解答下列问题:
竞赛成绩统计表(成绩满分100分)
组别
分数
人数
A组
4
B组
C组
10
D组
E组
14
合计
(1)、本次共调查了名学生;C组所在扇形的圆心角为度;(2)、该校共有学生1600人,若90分以上为优秀,估计该校优秀学生人数为多少?(3)、若E组14名学生中有4人满分,设这4名学生为E1 , E2 , E3 , E4 , 从其中抽取2名学生代表学校参加上一级比赛,请用列表或画树状图的方法求恰好抽到 , 的概率.25. 问题背景:在解决“半角模型”问题时,旋转是一种常用方法.如图①,在四边形ABCD中, , , , 点E,F分别是BC,CD上的点,且 , 连接EF,探究线段BE,EF,DF之间的数量关系. (1)、探究发现:小明同学的方法是将绕点A逆时针旋转120°至的位置,使得AB与AD重合,然后证明 , 从而得出结论:;(2)、拓展延伸:如图②,在正方形ABCD中,E、F分别在边BC、CD上,且 , 连接EF,(1)中的结论是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由.(3)、尝试应用:在(2)的条件下,若 , , 求正方形ABCD的边长.26. 如图
(1)、探究发现:小明同学的方法是将绕点A逆时针旋转120°至的位置,使得AB与AD重合,然后证明 , 从而得出结论:;(2)、拓展延伸:如图②,在正方形ABCD中,E、F分别在边BC、CD上,且 , 连接EF,(1)中的结论是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由.(3)、尝试应用:在(2)的条件下,若 , , 求正方形ABCD的边长.26. 如图 (1)、问题
(1)、问题如图1,在四边形ABCD中,点P为AB上一点,当时,求证: .
(2)、探究若将90°角改为锐角或钝角(如图2),其他条件不变,上述结论还成立吗?说明理由.
(3)、应用如图3,在中, , , 以点A为直角顶点作等腰 . 点D在BC上,点E在AC上,点F在BC上,且 , 若 , 求CD的长.