山东省菏泽市单县2021-2022学年九年级上学期期中数学试题

试卷更新日期：2022-09-23 类型：期中考试

进入出卷网下载

一、单选题

1. 60°角的正切值为（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\sqrt{3}$

查看试题解析
2. 在Rt△ABC中，∠C=90°，BC=3cm，AC=4cm，以点C为圆心，以2.5cm为半径画圆，则⊙C与直线AB的位置关系是（　　）

A、相交 B、相切 C、相离 D、不能确定

查看试题解析
3. 下列说法：①位似图形都相似；②位似图形都是平移后再放大(或缩小)得到；③直角三角形斜边上的中线与斜边的比为1：2；④两个相似多边形的面积比为4：9，则周长的比为16：81中，正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 在 $△$ ABC中， ${(2 c o s A - \sqrt{2})}^{2} + | 1 - t a n B | = 0$ ，则 $△$ ABC一定是（）

A、直角三角形 B、等腰三角形 C、等边三角形 D、等腰直角三角形

查看试题解析
5. 如图，直线AB $∥$ CD $∥$ EF，若AC=3，CE=4，则 $\frac{B D}{B F}$ 的值是（）

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、 $\frac{3}{7}$ D、 $\frac{4}{7}$

查看试题解析
6. 如图，四边形ABCD内接于⊙O，AD∥BC，BD平分∠ABC，∠A＝130°，则∠BDC的度数为（）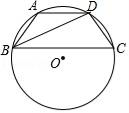

A、100° B、105° C、110° D、115°

查看试题解析
7. 如图，一渔船上的渔民在A处看见灯塔M在北偏东60°方向，这艘渔船以28km/时的速度向正东航行，半小时到B处，在B处看见灯塔M在北偏东15°方向，此时，灯塔M与渔船的距离是（）

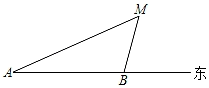A、7 $\sqrt{2}$ km B、14 $\sqrt{2}$ km C、7km D、14km

查看试题解析
8. 如图，在平行四边形ABCD中，AB＝6，AD＝9，∠BAD的平分线交BC于点E，交DC的延长线于点F，BG⊥AE于点G，BG＝4 $\sqrt{2}$ ，则△EFC的周长为（）

A、11 B、10 C、9 D、8

查看试题解析

二、填空题

9. 如果两个相似三角形的相似比为1：4，那么它们的面积比为．

查看试题解析
10. 在Rt△ABC中，∠C＝90°，AB＝10， $t a n A = \frac{3}{4}$ ，则BC的长是．

查看试题解析
11. 如图，在平面直角坐标系中，已知 $⊙ A$ 经过点 $E 、 B 、 O 、 C$ ，且点O为坐标原点，点C在y轴上，点E在x轴上，A(-3，2)，则 $t a n ∠ O B C =$ ．

查看试题解析
12.
将一副三角尺如图所示叠放在一起，则 $\frac{B E}{E C}$ 的值是．

查看试题解析
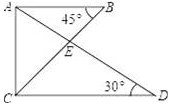
13. 如图，矩形ABCD的边长AB＝3cm，AC＝3 $\sqrt{5}$ cm，动点M从点A出发，沿AB以1cm/s的速度向点B匀速运动，同时动点N从点D出发，沿DA以2cm/s的速度向点A匀速运动．若△AMN与△ACD相似，则运动的时间t为s．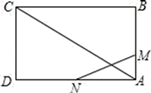

查看试题解析
14. 如图，在半径为6cm的⊙O中，点A是劣弧BC的中点，点D是优弧BC上一点，且∠D＝30°．下列四个结论：①OA⊥BC；②BC＝6 $\sqrt{3}$ cm；③sin∠AOB＝ $\frac{\sqrt{3}}{2}$ ；④四边形ABOC是菱形．其中正确的结论是． (填序号)

查看试题解析
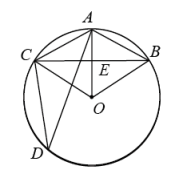15. 计算：tan30° $\cdot$ sin60°+cos²30°-sin²45°tan45°= ．

查看试题解析

三、解答题

16. 如图，在平行四边形ABCD中，点E在BC上，∠CDE＝∠DAE.

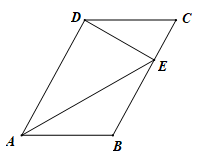(1)、求证： $△ A D E ∽ △ D E C$ ；

(2)、若AD＝6，DE＝4，求CE的长.

查看试题解析
17. 如图，在边长均为1的小正方形网格纸中，△ABC的顶点A、B、C均在格点上，O为直角坐标系的原点，点A（﹣1，0）在x轴上．

(1)、以O为位似中心，将△ABC放大，使得放大后的△A₁B₁C₁与△ABC的相似比为2：1，要求所画△A₁B₁C₁与△ABC在原点两侧；

(2)、分别写出点A₁、B₁、C₁的坐标．

查看试题解析
18. 如图，在△ABC中，DE∥BC，AD：DB＝2：1，△ABC的面积为27，求△ADE的面积．

查看试题解析
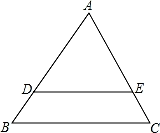19. 如图，AD与⊙O相切于点D，点A在直径CB的延长线上．

(1)、求证：∠DCB＝∠ADB；

(2)、若∠DCB＝30°，AC＝3 $\sqrt{3}$ ，求AD的长．

查看试题解析
20. 如图，在△ABC中，∠ACB= $90 °$ ，D为AC上一点，DE⊥AB于点E，AC=12，BC=5．

(1)、求 $cos ∠ A D E$ 的值；

(2)、当 $D E = D C$ 时，求 $A D$ 的长．

查看试题解析
21. 如图，AD是△ABC外角∠EAC的平分线，AD与△ABC的外接圆⊙O交于点D．

(1)、求证：DB＝DC；

(2)、若∠CAB＝30°，BC＝4，求劣弧 $\overset{⌢}{D C}$ 的长度．

查看试题解析
22. 如图，在斜坡PA的坡顶平台处有一座信号塔BC，在坡顶A处测得该塔的塔顶B的仰角为76°，在坡底的点P处测得塔顶B的仰角为45°，已知斜坡长PA＝26m，坡度为1：2.4，点A与点C在同一水平面上，且AC $/ /$ PQ，BC⊥AC．请解答以下问题：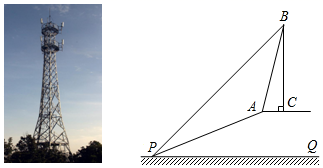

(1)、求坡顶A到地面PQ的距离；

(2)、求信号塔BC的高度．（结果精确到1m，参考数据：sin76°≈0.97，cos76°≈0.24，tan76°≈4.00）

查看试题解析
23. 如图，在△ABC中，AB＝AC，以AB为直径的⊙O分别与BC，AC交于点D，E，过点D作DF⊥AC，垂足为点F．

(1)、求证：直线DF是⊙O的切线；

(2)、求证：BC²＝4CF•AC；

(3)、若⊙O的半径为4，∠CDF＝15°，求阴影部分的面积．

查看试题解析
24. 如图

(1)、某学校“智慧方园”数学社团遇到这样一个题目：
如图1，在△ABC中，点O在线段BC上，∠BAO=30°，∠OAC=75°，AO= $3 \sqrt{3}$ ，BO：CO=1：3，求AB的长．
经过社团成员讨论发现，过点B作BD∥AC，交AO的延长线于点D，通过构造△ABD就可以解决问题（如图2）．
请回答：∠ADB=°，AB= ．

(2)、请参考以上解决思路，解决问题：
如图3，在四边形ABCD中，对角线AC与BD相交于点O，AC⊥AD，AO= $3 \sqrt{3}$ ，∠ABC=∠ACB=75°，BO：OD=1：3，求DC的长．

查看试题解析