2022年秋季湘教版数学九年级上册第一章 《反比例函数》单元检测B
试卷更新日期:2022-09-22 类型:单元试卷
一、单选题(每题3分,共30分)
-
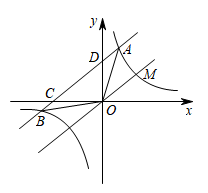
1. 反比例函数y= 的图象分别位于( )A、第一、第三象限 B、第一、第四象限 C、第二、第三象限 D、第二、第四象限2. 正比例函数y=2x与反比例函数y= 的图象或性质的共有特征之一是( )A、函数值y随x的增大而增大 B、图象在第一、三象限都有分布 C、图象与坐标轴有交点 D、图象经过点(2,1)3. 在同一平面直角坐标系中,函数与 (k为常数且)的图象大致是( )A、
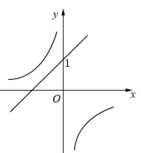 B、
B、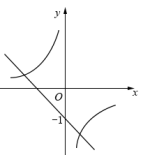 C、
C、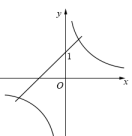 D、
D、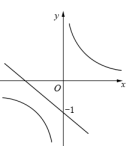 4. 一次函数y=mx+n的图象与反比例函数y= 的图象交于点A、B,其中点A、B的坐标为A(- ,-2m)、B(m,1),则△OAB的面积( )A、3 B、 C、 D、5. 地球周围的大气层阻挡了紫外线和宇宙射线对地球生命的伤害,同时产生一定的大气压,海拔不同,大气压不同,观察图中数据,你发现,正确的是( )
4. 一次函数y=mx+n的图象与反比例函数y= 的图象交于点A、B,其中点A、B的坐标为A(- ,-2m)、B(m,1),则△OAB的面积( )A、3 B、 C、 D、5. 地球周围的大气层阻挡了紫外线和宇宙射线对地球生命的伤害,同时产生一定的大气压,海拔不同,大气压不同,观察图中数据,你发现,正确的是( ) A、海拔越高,大气压越大 B、图中曲线是反比例函数的图象 C、海拔为4千米时,大气压约为70千帕 D、图中曲线表达了大气压和海拔两个量之间的变化关系6. 如图,正比例函数y=ax(a为常数,且a≠0)和反比例函数y=(k为常数,且k≠0)的图象相交于A(﹣2,m)和B两点,则不等式ax>的解集为( )
A、海拔越高,大气压越大 B、图中曲线是反比例函数的图象 C、海拔为4千米时,大气压约为70千帕 D、图中曲线表达了大气压和海拔两个量之间的变化关系6. 如图,正比例函数y=ax(a为常数,且a≠0)和反比例函数y=(k为常数,且k≠0)的图象相交于A(﹣2,m)和B两点,则不等式ax>的解集为( )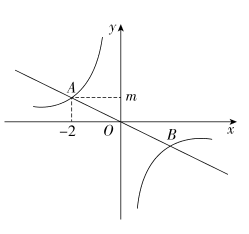 A、x<﹣2或x>2 B、﹣2<x<2 C、﹣2<x<0或x>2 D、x<﹣2或0<x<27. 如图,在平面直角坐标系中,点M为x轴正半轴上一点,过点M的直线l∥y轴,且直线l分别与反比例函数和的图象交于P、Q两点.若S△POQ=15,则k的值为( )
A、x<﹣2或x>2 B、﹣2<x<2 C、﹣2<x<0或x>2 D、x<﹣2或0<x<27. 如图,在平面直角坐标系中,点M为x轴正半轴上一点,过点M的直线l∥y轴,且直线l分别与反比例函数和的图象交于P、Q两点.若S△POQ=15,则k的值为( )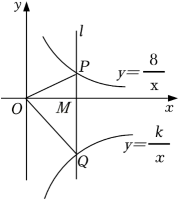 A、38 B、22 C、﹣7 D、﹣228. 如图,正方形 的顶点分别在反比例函数 和 的图象上.若 轴,点 的横坐标为3,则 ( )
A、38 B、22 C、﹣7 D、﹣228. 如图,正方形 的顶点分别在反比例函数 和 的图象上.若 轴,点 的横坐标为3,则 ( )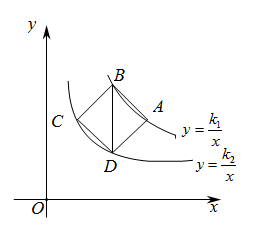 A、36 B、18 C、12 D、99. 如图,直线AB交x轴于点C,交反比例函数y=(a>1)的图象于A、B两点,过点B作BD⊥y轴,垂足为点D,若S△BCD=5,则a的值为( )
A、36 B、18 C、12 D、99. 如图,直线AB交x轴于点C,交反比例函数y=(a>1)的图象于A、B两点,过点B作BD⊥y轴,垂足为点D,若S△BCD=5,则a的值为( ) A、8 B、9 C、10 D、1110. 如图,在同一平面直角坐标系中,直线y=t(t为常数)与反比例函数y1 ,y2 的图象分别交于点A,B,连接OA,OB,则△OAB的面积为( )
A、8 B、9 C、10 D、1110. 如图,在同一平面直角坐标系中,直线y=t(t为常数)与反比例函数y1 ,y2 的图象分别交于点A,B,连接OA,OB,则△OAB的面积为( )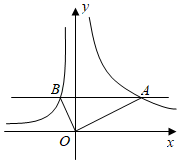 A、5t B、 C、 D、5
A、5t B、 C、 D、5二、填空题(每题3分,共18分)
-
11. 反比例函数与一次函数交于点 , 则k的值为.12. 根据物理学知识,在压力不变的情况下,某物体承受的压强是它的受力面积的反比例函数,其函数图象如图所示,当时,该物体承受的压强p的值为 Pa.
 13. 如图四边形ABCD是平行四边形,CD在x轴上,点B在y轴上,反比例函数的图象经过第一象限点A,且平行四边形ABCD的面积为6,则 .
13. 如图四边形ABCD是平行四边形,CD在x轴上,点B在y轴上,反比例函数的图象经过第一象限点A,且平行四边形ABCD的面积为6,则 .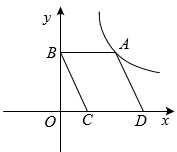 14. 如图,在平面直角坐标系中,一次函数的图象经过点且与函数的图象交于点.若一次函数随的增大而增大,则的取值范围是.
14. 如图,在平面直角坐标系中,一次函数的图象经过点且与函数的图象交于点.若一次函数随的增大而增大,则的取值范围是.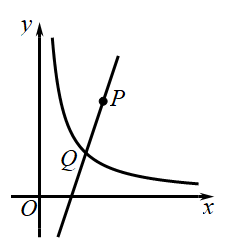 15. 已知点A在反比例函数的图象上,点B在x轴正半轴上,若为等腰三角形,且腰长为5,则的长为 .
15. 已知点A在反比例函数的图象上,点B在x轴正半轴上,若为等腰三角形,且腰长为5,则的长为 . 16. 如图,已知直角三角形中, , 将绕点点旋转至的位置,且在的中点,在反比例函数上,则的值为 .
16. 如图,已知直角三角形中, , 将绕点点旋转至的位置,且在的中点,在反比例函数上,则的值为 .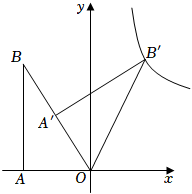
三、解答题(共8题,共72分)
-
17. 密闭容器内有一定质量的气体,当容器的体积(单位:)变化时,气体的密度(单位:)随之变化.已知密度与体积是反比例函数关系,它的图像如图所示.
 (1)、求密度关于体积的函数解析式;(2)、当时,求该气体的密度 .18. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象都经过两点.
(1)、求密度关于体积的函数解析式;(2)、当时,求该气体的密度 .18. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象都经过两点.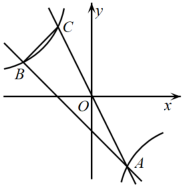 (1)、求反比例函数和一次函数的表达式;(2)、过O、A两点的直线与反比例函数图象交于另一点C,连接BC,求的面积.19. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于点 , 与轴交于点 .
(1)、求反比例函数和一次函数的表达式;(2)、过O、A两点的直线与反比例函数图象交于另一点C,连接BC,求的面积.19. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于点 , 与轴交于点 .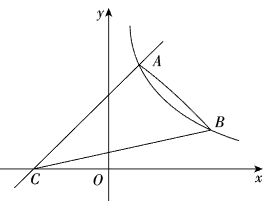 (1)、求点的坐标和反比例函数的解析式;(2)、点是反比例函数图象上一点且纵坐标是1,连接 , , 求的面积.20. 如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与反比例函数y=(m为常数,m≠0)的图象在第二象限交于点A(﹣4,3),与y轴负半轴交于点B,且OA=OB
(1)、求点的坐标和反比例函数的解析式;(2)、点是反比例函数图象上一点且纵坐标是1,连接 , , 求的面积.20. 如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与反比例函数y=(m为常数,m≠0)的图象在第二象限交于点A(﹣4,3),与y轴负半轴交于点B,且OA=OB (1)、求反比例函数和一次函数的解析式.(2)、根据图象直接写出当x<0时,不等式kx+b≤的解集.21. 如图,直线与反比例函数的图象相交于点 , , 已知点的纵坐标为6
(1)、求反比例函数和一次函数的解析式.(2)、根据图象直接写出当x<0时,不等式kx+b≤的解集.21. 如图,直线与反比例函数的图象相交于点 , , 已知点的纵坐标为6 (1)、求的值;(2)、若点是轴上一点,且的面积为3,求点的坐标.22. 如图, , , 点A,B分别在函数()和()的图象上,且点A的坐标为.
(1)、求的值;(2)、若点是轴上一点,且的面积为3,求点的坐标.22. 如图, , , 点A,B分别在函数()和()的图象上,且点A的坐标为.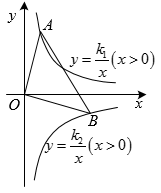 (1)、求 , 的值:(2)、若点C,D分在函数()和()的图象上,且不与点A,B重合,是否存在点C,D,使得 , 若存在,请直接出点C,D的坐标:若不存在,请说明理由.
(1)、求 , 的值:(2)、若点C,D分在函数()和()的图象上,且不与点A,B重合,是否存在点C,D,使得 , 若存在,请直接出点C,D的坐标:若不存在,请说明理由.