2022年苏科版初中数学七年级上册 4.2 解一元一次方程(1) 同步练习
试卷更新日期:2022-09-22 类型:同步测试
一、夯实基础
-
1. 方程的解是( )A、 B、 C、 D、2. 若 是关于x的方程 的解,则m的值是( )A、1 B、-1 C、 D、3. 已知关于x的方程2x+a=1-x与方程2x-3=1的解相同,则a的值为( )A、2 B、-2 C、5 D、-54. 已知关于 的方程 的解是 ,则 的值是( )A、 B、 C、 D、5. 根据等式的性质,下列变形错误的是( ).A、如果 ,那么 B、如果 ,那么 C、如果 ,那么 D、如果 ,那么6. 已知 , 则a的相反数是.7. 如果2a+4=a-3,那么式子的值是 .8. 方程 和方程 的解相同,则 = .9. 当x=时,代数式6x+1与-2x-5的值互为相反数。10. 单项式与的差仍是单项式,则.11. 已知2x-12与x+3互为相反数,求x的值.12. 如图是一个正方体的展开图,折成正方体后相对面上的两个数之和都相等,求的值.
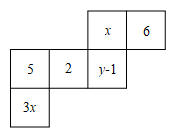 13. 定义新运算: , , 等式右边是通常的加法、减法运算;(1)、求的值;(2)、化简:;(3)、若 , 求x的值.
13. 定义新运算: , , 等式右边是通常的加法、减法运算;(1)、求的值;(2)、化简:;(3)、若 , 求x的值.二、能力提优
-
14. 当时,关于的方程的解为( )A、 B、 C、 D、15. 当k取何值时,与的解相同( )A、16 B、 C、4 D、1216. 若代数式5﹣4x与 的值相等,则x的值是( )A、 B、 C、1 D、17. 已知(k-1)x|k|+3=0是关于x的一元一次方程.则此方程的解是( )A、 B、 C、 D、18. 已知 有最大值,则方程 的解是
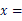 ( ) A、 B、 C、- D、-19. 若关于x的方程3x﹣7=2x+a的解与方程4x+3=﹣5的解互为倒数,则a的值为.20. 已知关于x的方程3a-x= +3的解为2,则代数式a2-2a+1的值是。21. 若关于 的方程 是一元一次方程,则方程的解为.22. 当代数式 有最大值时,关于x的方程 的解为.23. 已知关于x的方程x﹣5=﹣mx有整数解,则正整数m的值为.24. 当x取什么数时, 与 互为相反数。25. 若 ,且 ,求 的值.26. 已知 为整数,且满足关于x的方程(2m+1)x=3mx-1,(1)、当 时,求方程的解;(2)、该方程的解能否为3,请说明理由;(3)、当x为正整数时,请求出的m值.27. 历史上的数学巨人欧拉最先把关于 的多项式用记号 来表示,即 ,例如:当 时,多项式 的值记为 =1。(1)、已知 ,分别求出 和 的值。(2)、已知 , ,求 的值。
( ) A、 B、 C、- D、-19. 若关于x的方程3x﹣7=2x+a的解与方程4x+3=﹣5的解互为倒数,则a的值为.20. 已知关于x的方程3a-x= +3的解为2,则代数式a2-2a+1的值是。21. 若关于 的方程 是一元一次方程,则方程的解为.22. 当代数式 有最大值时,关于x的方程 的解为.23. 已知关于x的方程x﹣5=﹣mx有整数解,则正整数m的值为.24. 当x取什么数时, 与 互为相反数。25. 若 ,且 ,求 的值.26. 已知 为整数,且满足关于x的方程(2m+1)x=3mx-1,(1)、当 时,求方程的解;(2)、该方程的解能否为3,请说明理由;(3)、当x为正整数时,请求出的m值.27. 历史上的数学巨人欧拉最先把关于 的多项式用记号 来表示,即 ,例如:当 时,多项式 的值记为 =1。(1)、已知 ,分别求出 和 的值。(2)、已知 , ,求 的值。三、延伸拓展
-
28. 如果四个不同的正整数 , , , 满足 ,则 等于( )A、 B、 C、 D、29. 观察下列两个等式: , ,给出定义如下:我们称使等式a+b=ab-1成立的一对有理数a,b为“一中有理数对”,记为(a,b),如:数对(3,2), 都是“一中有理数对”.(1)、数对(-2,1), 中是“一中有理数对”的是 .(2)、若(a,3)是“一中有理数对”,求a的值;(3)、若(m,n)是“一中有理数对”,则(-n,-m)是否为“一中有理数对”?请说明理由.30. 如图,已知在数轴上有三个点A、B、C,O是原点,满足OA=AB=BC=20cm,动点P从点O出发向右以每秒2cm的速度匀速运动;同时,动点Q从点C出发,在数轴上向左匀速运动,速度为v(v>1);运动时间为t.
 (1)、求:点P从点O运动到点C时,运动时间t的值.(2)、若Q的速度v为每秒3cm,那么经过多长时间P,Q两点相距30cm?此时|QB﹣QC|是多少?(3)、当|PA+PB|=2|QB﹣QC|=24时,请直接写出点Q的速度v的值.
(1)、求:点P从点O运动到点C时,运动时间t的值.(2)、若Q的速度v为每秒3cm,那么经过多长时间P,Q两点相距30cm?此时|QB﹣QC|是多少?(3)、当|PA+PB|=2|QB﹣QC|=24时,请直接写出点Q的速度v的值.