天津市红桥区2021-2022学年九年级上学期期中考试数学试卷
试卷更新日期：2022-09-22 类型：期中考试
一、单选题
-
1. 下列方程中，是一元二次方程的是（ ）A、4（x＋2）＝25 B、2x2＋3x－1＝0 C、x＋y＝0 D、＝42. 下列图形中，可以看作是中心对称图形的是（ ）A、
B、
C、
D、
3. 一元二次方程3x2－6x＝1化为－般形式ax2＋bx＋c＝0（a≠0）后，a，b，c的值分别是（ ）A、a＝3，b＝6，c＝1 B、a＝3，b＝－6，c＝1 C、a＝－3，b＝－6，c＝1 D、a＝3，b＝－6，c＝－14. 一元二次方程（x＋1）2＝2可以转化为两个一元一次方程，其中一个一元一次方程为x＋1＝ ， 则另一个一元一次方程为（ ）A、x－1＝ B、x＋1＝2 C、x＋1＝－ D、x＋1＝－25. 用配方法解方程x2－8x＋1＝0时，配方所得的方程为（ ）A、（x－4）2＝15 B、（x－4）2＝17 C、（x＋4）2＝15 D、（x－8）2＝156. 已知关于x的一元二次方程x2＋px＋q＝0的两根分别为x1＝－4，x2＝7，则原方程可化为（ ）A、（x－4）（x－7）＝0 B、（x＋4）（x＋7）＝0 C、（x－4）（x＋7）＝0 D、（x＋4）（x－7）＝07. 关于x的一元二次方程ax2＋bx＋c＝0（a≠0）的两个根分别为－1和5，则二次函数y＝ax2＋bx＋c（a≠0）的对称轴是（ ）A、x＝－3 B、x＝－1 C、x＝2 D、x＝38. 若点A（－1，y1），B（0，y2），C（1，y3）都在二次函数y＝2x2＋x－1的图象上，则y1 ， y2 ， y3的大小关系是（ ）A、y1＜y2＞＜y3 B、y2＜y1＜y3 C、y3＜y1＜y2 D、y3＜y2＜y19. 参加一次商品交易会的每两家公司之间都签订了一份合同，所有公司共同签订了45份合同．设共有x家公司参加商品交易会，则x满足的关系式为（ ）A、 x(x＋1)＝45 B、 x(x－1)＝45 C、x(x＋1)＝45 D、x(x－1)＝4510. 如图，将△ABC绕点A逆时针旋转得到△ADE，使点A，B，E在一条直线上，点B的对应点为D，点C的对应点为E，连接BD，CE，则下列结论一定正确的是（ ）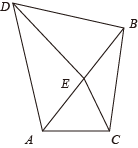
A、AD＝AC B、BC＝DE C、∠AED＝∠BEC D、BD∥AC11. 一个直角三角形的两直角边之和为14cm，面积是24cm2 ， 则斜边的长度为（ ）A、6cm B、8cm C、10cm D、12cm12. 抛物线 的对称轴是直线 ，与x轴的一个交点为 ， ，下列结论：① ；② ；③ ，其中正确结论的个数是（ ）A、0个 B、1个 C、2个 D、3个二、填空题
-
13. 在平面直角坐标系中，O为原点，将点A（2，0）绕点O逆时针旋转180°得点A′，则点A′的坐标为 ．14. 二次函数的最小值是 ．15. 若关于x的一元二次方程可以配方成（x－2）2－4＝0的形式，则该方程的两根之和为 ．16. 若m≠0，则关于x的一元二次方程mx2＋x－3m＝0的实数根的个数为 ．17. 某地区2018年的人均收入为10万元，2020年的人均收入为14.4万元，则人均收入的年平均增长率为 ．18. 当k－2≤x≤k时，函数y＝x2－4x＋4（k为常数）的最小值为4，则k的值是 ．
三、解答题
-
19. 在平面直角坐标系中，△ABC各顶点的坐标分别为A（－3，2），B（4，1），C（0，－3）．请在图中作出△ABC关于原点对称的△A′B′C′，并写出△A′B′C′各顶点的坐标．
20. 解下列关于x的方程．(1)、x2－5x＋1＝0；(2)、（2x＋1）2－25＝0．21. 已知关于x的一元二次方程3x2﹣2x﹣m＝0（m为常数）．(1)、若x＝3是该方程的一个实数根，求m的值；(2)、当m＝1时，求该方程的实数根；(3)、若该方程有两个不相等的实数根，求m的取值范围．22. 已知二次函数y＝x2－2x－3的图象为抛物线C．(1)、写出抛物线C的开口方向、对称轴和顶点坐标；(2)、当2≤x≤4时，求该二次函数的函数值y的取值范围；(3)、将抛物线C先向右平移2个单位长度，得到抛物线C1；再将抛物线C1向下平移1个单位长度，得到抛物线C2 ， 请直接写出抛物线C1 ， C2对应的函数解析式．23. 已知矩形ABCD的周长为20，设AB的长为x，矩形的面积为S．(1)、写出S关于x的函数解析式，并写出x的取值范围；(2)、当矩形ABCD的面积为24时，求AB的长；(3)、当AB的长为多少时，矩形ABCD的面积最大？最大面积是多少？
